흐름

• 가장 중요한 핵심 단어는?
  

• RNNLM(Recursive-Neural-Network Language Model)은 언어모델이다.

• '언어 모델'은 입력 단어의 다음에 어떤 단어가 올 지 예측하는 모델이다.

• 다음 단어가 올 지 예측하기 위해서는 이전 문맥이 중요하다. 하나의 단어만 가지고는 판단할 수 없기 때문이다.
  예) 나는 사과를 000.
  빈 칸에 들어갈 말로 유추할 수 있는 단어는
  샀다
  먹었다
  씻었다
  등등... 앞의 단어들과 상호작용했을 때 가장 어울리는 단어들이 올 것으로 예상이 된다. 주어진 단어(문맥)가 많을수록 빈 칸에 올 단어는 하나로 특정될 것이다.

• 이전 단어를 기억하는 모델은 대표적으로 RNN이 있다. R은 Recursive의 약자인데 재귀적이고 순환적이라는 의미이다.

• 무엇이 순환될까? 은닉 상태 벡터이다. hidden layer로 많이 쓰인다.

• hidden layer에는 어떤 정보가 담겨 있을까?

• $h_t = tanh(h_{t-1}W_h + x_tW_x + b)$이 공식은 은닉 상태 벡터를 결정하는 식인데 이전 시점의 은닉 상태와 은닉층의 가중치, 현 시점의 입력 단어와 입력층의 가중치, 그리고 편향이 필요하다.

• 어떻게 은닉 상태 벡터가 순환이 될까?

• 순환은 처음과 끝이 같은 연결 리스트로 볼 수 있다. 여러 요소들이 연결되어있고 순차적으로 가다보면 처음으로 다시 돌아오게 되는 ring💍 형식이 순환이다.
  

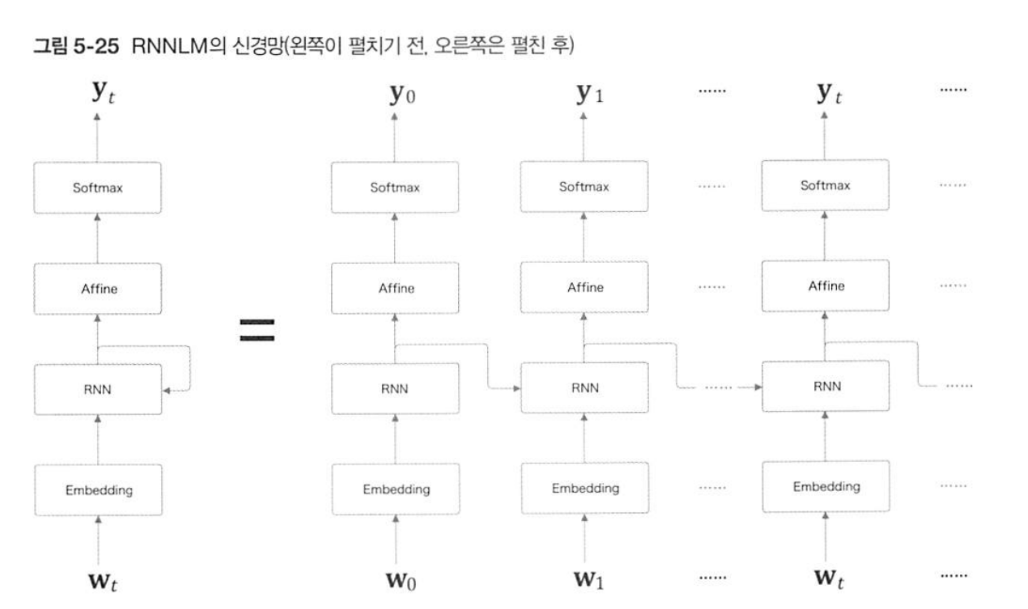
• 바로 이런 식으로 이전 시점의 은닉 상태 벡터($h_{t-1}$)가 다음 시점으로 계속해서 이동하면서 순환이 시작된다.

• 은닉 상태 벡터가 처음으로 다시 돌아오는 것은 '역전파'를 통해 이루어진다.

• 역전파는 딥러닝 학습에 필수적인 과정으로, 정답과 모델의 답이 얼마나 차이나는지를 확인한 다음 그 차이를 줄이는 방향으로 파라미터를 조정하는 것이다.

• 역전파는 한 번의 순전파 이후 예측한 답과 정답을 비교하여 loss 함수로 점수를 매긴다.

• 이 점수를 다시 역방향으로 연산하며 가중치와 편향 값을 바꾼다.

• 이 과정을 담은 그래프이다.
  

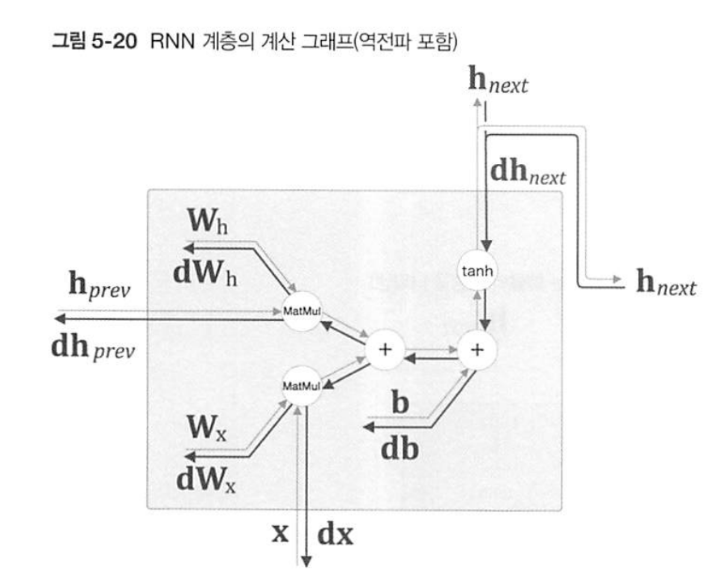
• 역전파는 가중치와 편향을 정답에 가깝도록 변경하는 것이 목표이다. 즉, loss를 줄이는 것이다.

• loss함수를 간단하게 최고차항의 계수가 양수인 이차함수라고 생각해보자.
  

• 최소값에 다다르기 위해서는 기울기가 감소하는 방향으로 값을 조정해야 한다.

• 이 때 기울기는 보통 손실함수를 가중치나 편향에 대하 미분한 값이다.

• 이는 각각 가중치, 편항이 손실함수에 미치는 영향을 나타낸다.

• 가중치/편향에 따른 손실함수의 증감량인 것이다.

• 새 가중치 = 기존 가중치 - η * 손실함수를 가중치로 미분한 값

• η는 learning rate로, 빨간 점들의 이동 보폭을 의미한다. 너무 크게 잡으면 loss 최저점을 지나칠 수 있으며 너무 작게 잡으면 학습 속도가 오래 걸린다.

• 새 가중치를 구하기 위해 기존 가중치에서 η와 gradient를 곱한 값을 '뺄셈'하는 이유는, gradient의 방향이 loss의 증가방향이기 때문이다.

• 위 과정을 반복하며 가중치와 편향을 업데이트하여 성능을 높일 수 있다.

• 위 과정을 오차역전파법이라하는데, RNN에서는 특별히 BPTT(Backpropagation Through Time) 즉 시간에 따른 오차역전파법이라고 부른다.

• RNN의 신경망은 다음과 같이 길게 늘어져있다.
  

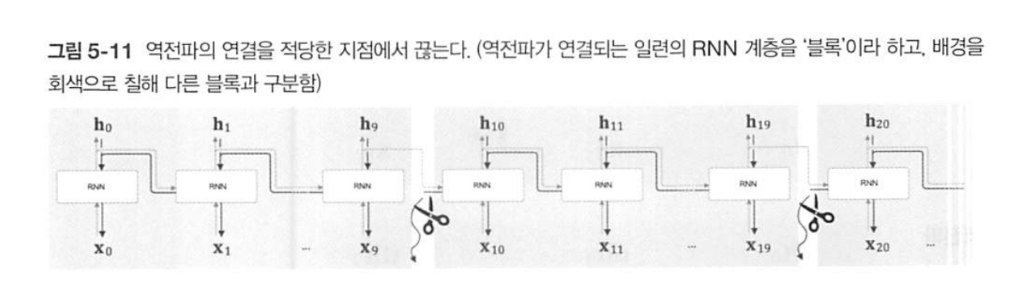
• 이렇게 한 번의 순전파-역전파가 너무 길면 역전파를 위해서 순전파 결과를 시점마다 중간결과를 모두 저장해야 하는데 메모리를 너무 많이 쓴다는 문제가 있다.

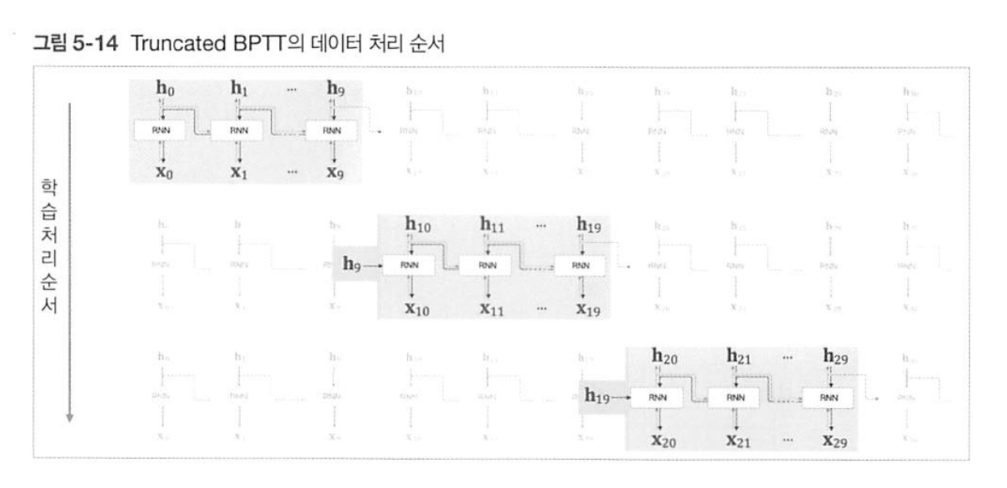
• 이를 해결하기 위해 일정 단위로 역전파 구간을 자른 것이 Truncated BPTT이다.

• 이 때 순전파는 정보가 단절되어서도 안되고, 구간을 잘랐다 해도 순서가 바뀌어선 안된다.

• 어떤 말의 내용을 앞뒤를 삭제하거나 단어의 순서를 뒤바꿨을 때 전혀 다른 의미가되는 것을 생각해보면 납득이 된다.
  

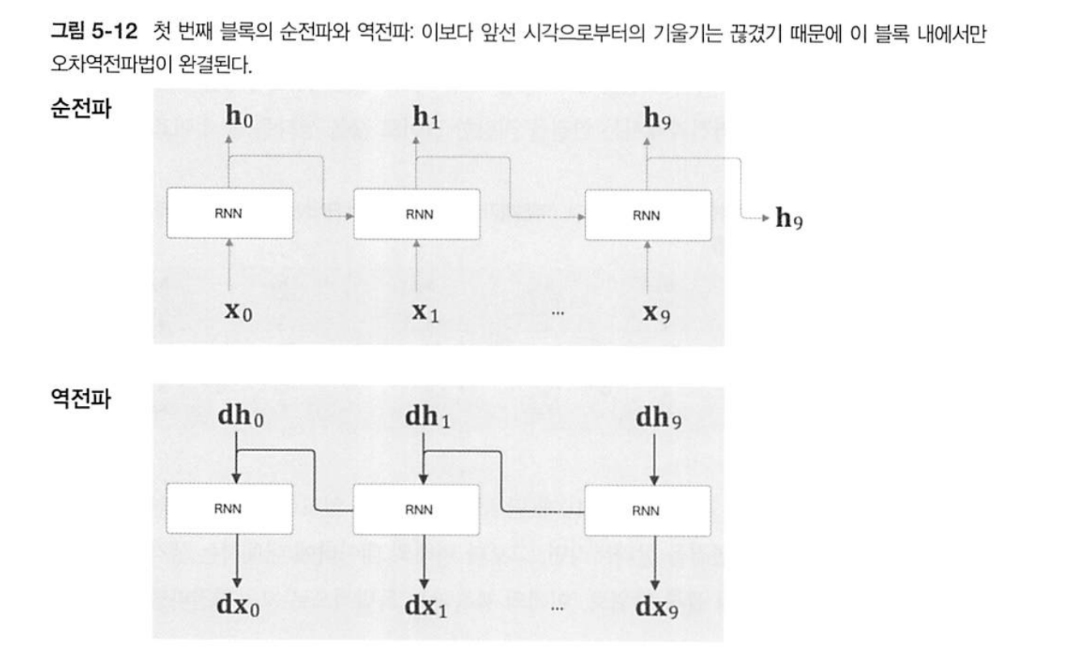
• 한 단위에서 순전파와 역전파를 이어서 하는 이유는 메모리를 적게 쓰는 대신 순전파에서 나오는 $h_t$를 바로바로 쓰기 때문이다.

• 하지만 위의 계산이 끝났다 해서 바로 $h_t$를 지울 수는 없다.

• 다음 시점에서 순전파할 때 바로 전 $h_t$값이 필요하기 때문이다.
  

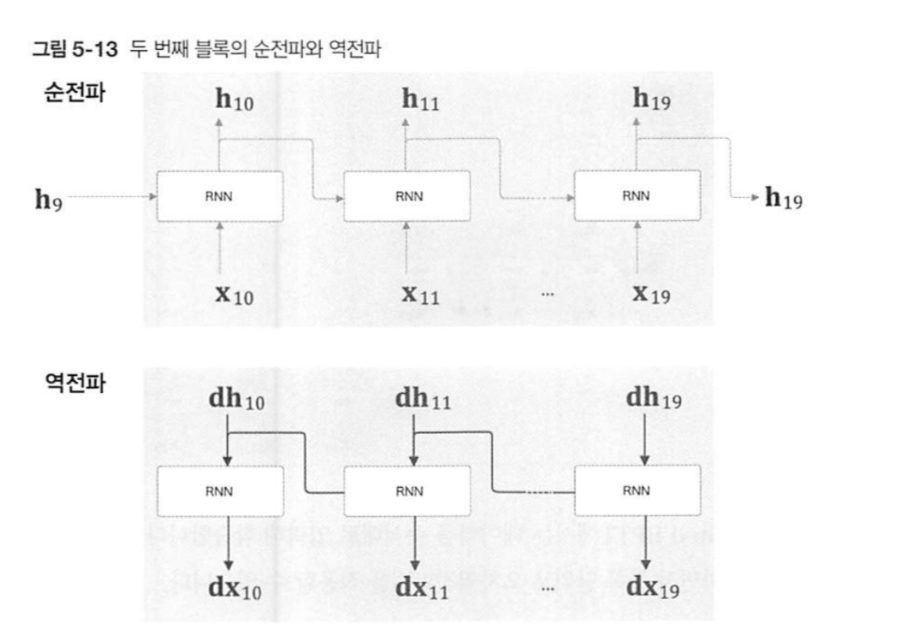
• 이제 $h_t$를 지울 수 있다.

• 이런 식으로 두 단위 당 하나의 $h_t$만 저장하는 식으로 이어나가면 이런 그림이 완성된다.
  

• 凸모양처럼 삐져나온 저 $h_9$와 $h_{19}$가 Truncated BPTT의 핵심이다.

• Truncated BPTT는 미니 배치 처리 방식으로 구현할 수 있다.

• 추가로 메모리 절약을 위해 미니 배치에 여러 동일 길이의 다른 시점(단, 최대한 덜 연속적이게)블록을 묶어서 처리할 수 있다.
  

• 메모리 상에는 두 쌍의 RNN 아키텍처가 돌아가고 있을 것이다. 그 결과로 은닉 상태 벡터가 출력이 될 것이고 이는 임시 저장된다.
  미니배치 하나에 대한 처리가 끝났으면 다음 미니배치로 넘어간다. 아까 임시로 저장해둔 은닉 상태 벡터 두 개를 미니배치의 단어벡터와 함께 입력해서 두 번째로 RNN의 아키텍처를 돌린다. 이를 반복한다.

• 이 아키텍처를 Time RNN이라고 부를 것이다. Time RNN은 기존 RNN과 같은 구조이지만 입력, 출력 데이터가 벡터인 것이 다른 점이다.
  

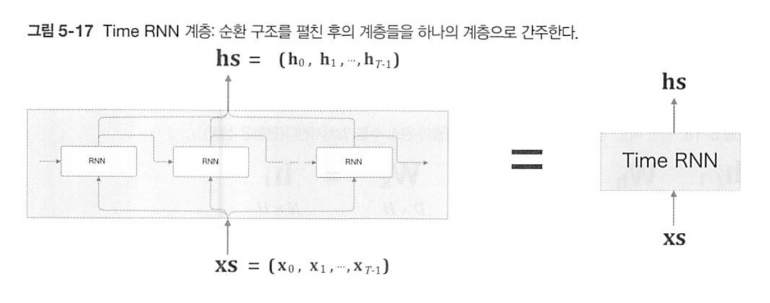
• 다음은 Time RNN 코드이다.

class RNN:
    def __init__(self, Wx, Wh, b):
        self.params = [Wx, Wh, b]
        self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
        self.cache = None

    def forward(self, x, h_prev):
        Wx, Wh, b = self.params
        t = np.matmul(h_prev, Wh) + np.matmul(x, Wx) + b
        h_next = np.tanh(t)
        self.cache = (x, h_prev, h_next)
        return h_next

• 초기화 함수로 Wx, Wh, b를 받고 있다. 각각은 입력 가중치, 은닉 가중치, 편향이다.
  - params 속성에 입력값을 리스트로 저장한다.
  - grads 속성을 초기화한다. shape은 Wx, Wh, b를 따른다.
  - 중간 결과를 저장할 cache 속성을 초기화한다.

rnn = RNN(Wx, Wh, b)

• 클래스를 호출할 때 위와 같이 입력해주면 된다.
• forward 메서드의 입력값은 x, h_prev으로 단어벡터와 이전 시점의 은닉 상태이다.
  - class를 호출할 때 사용자가 입력한 Wx, Wh, b값을 변수에 저장한다.
  - t와 h_next는 RNN 공식을 그대로 구현한 것이다. np.matmul은 행렬곱 함수이다.
  - 순전파 결과와 입력값을 self.cache인스턴스에 저장한다. 이는 바로 이어질 역전파에 쓰인다.

def backward(self, dh_next):
    Wx, Wh, b = self.params
    x, h_prev, h_next = self.cache

    dt = dh_next * (1 - h_next ** 2)
    db = np.sum(dt, axis=0)
    dWh = np.matmul(h_prev.T, dt)
    dh_prev = np.matmul(dt, Wh.T)
    dWx = np.matmul(x.T, dt)
    dx = np.matmul(dt, Wx.T)

    self.grads[0][...] = dWx
    self.grads[1][...] = dWh
    self.grads[2][...] = db

    return dx, dh_prev

• 위 코드는 TimeRNN에서 역전파를 구현한 메서드이다.