목차
- 쌍곡함수
- RNN의 계산 그래프
- RNNLM(RNN Language Model)
- BPTT
- Truncated BPTT
- RNN 구현
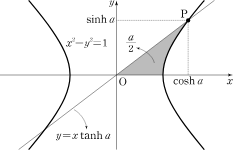
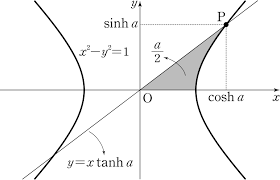
쌍곡함수(Hyperbolic function)
- 삼각함수는 원과 관련이 있다.
- 이와 유사하게 쌍곡선 함수를 만들 수 있다.
정의
1)
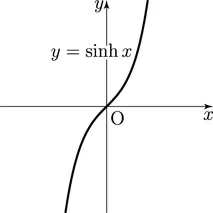
2)
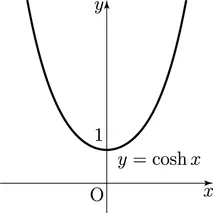
3) =
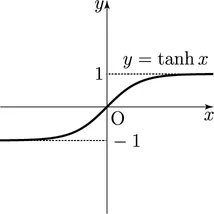
공식
삼각함수 기본 공식
1)
2)
hyperbolic 삼각함수 기본식
1)
2)도함수
1)
2)
3)
증명
.
.
.
.
.
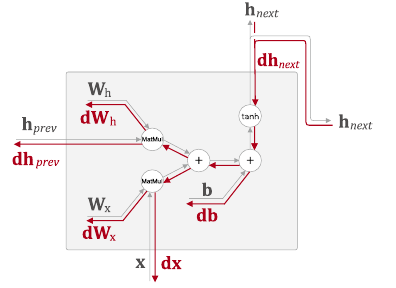
RNN의 계산 그래프
-
위 계산그래프는 다음 식을 그래프로 나타낸 것이다.
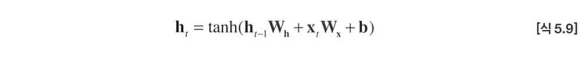
[출처:밑바닥부터 시작하는 딥러닝2 사이토 고기토 저] -
이처럼 계산식을 그래프로 나타내면 역전파 계산이 용이해진다.
계산그래프의 역전파 과정
- : 이하 로 불리며 다음 시점의 은닉 상태 벡터의 미분. 을 지나 다음 노드로 역전파된다.
- 는 를 지나 가 된다.
- 여기서 는 RNN 계산식의 일부인 을 의미한다.
출처: Kyung Hoon Han's Home
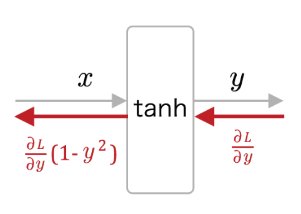
를 역전파 계산하면 가 들어가서
의 미분인 를 곱하고 다음 층으로 전달된다.
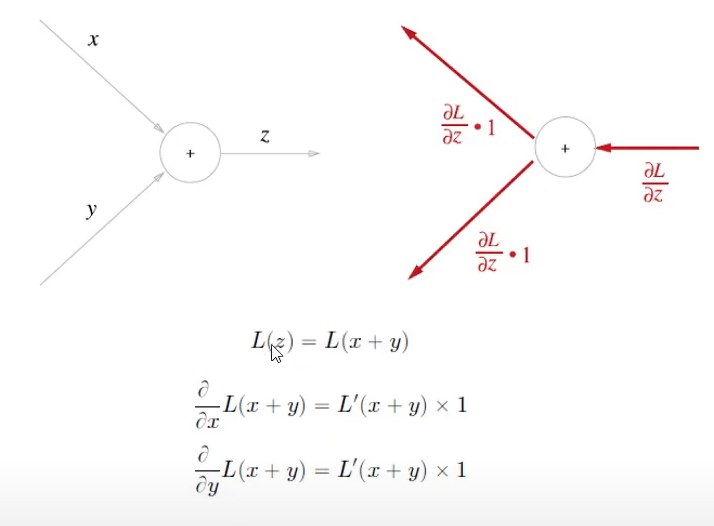
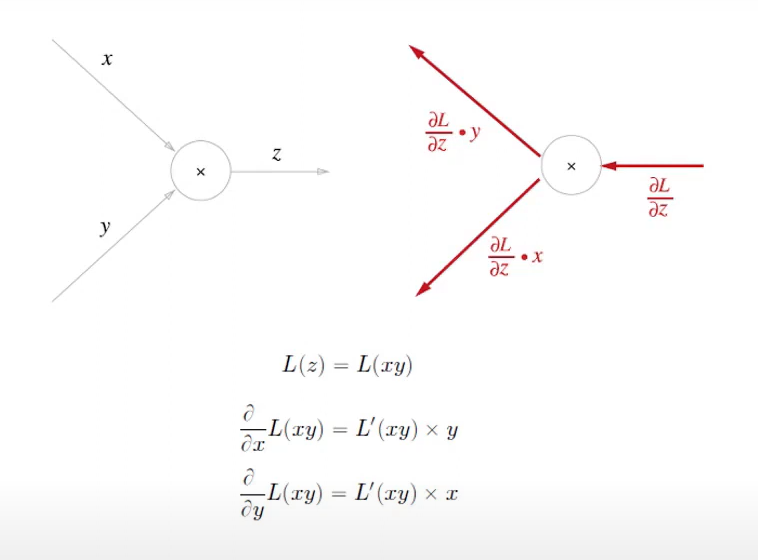
역전파의 규칙
- 1부터 시작한다.
- 계산그래프상에서는 다음과 같이 쉽게 표현 가능하다.
- 덧셈은 변화가 없다.
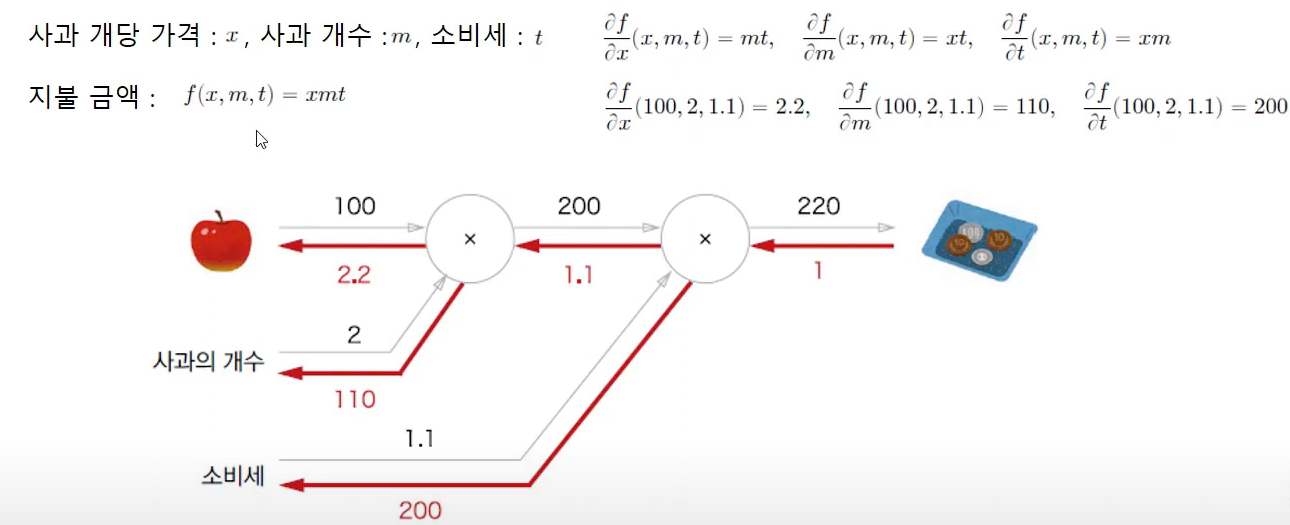
- 곱셈은 흘러들어온 값에 와 자리를 교차하여 곱해준다.
- 를 로 미분하는 것은 사과 가격에 따른 전체 가격의 변동량(변화량)을 의미한다.
- 여기서 L은 Loss 즉 손실함수를 뜻하며 대체로 CEE(Cross Entropy Error)함수를 많이 사용한다.
: 교차 엔트로피 오차
: 데이터의 인덱스
: 실제값 (참값)
: 모델의 예측값 (출력값)
RNNLM(RNN Language Model)
BPTT(Back Propagation Through Time)
Truncated BPTT
RNN 구현
RNN
class RNN:
def __init__(self, Wx, Wh, b):
self.params = [Wx, Wh, b]
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
self.cache = None
def forward(self, x, h_prev):
Wx, Wh, b = self.params
t = np.dot(h_prev, Wh) + np.dot(x, Wx) + b
h_next = np.tanh(t)
self.cache = (x, h_prev, h_next)
return h_next
def backward(self, dh_next):
Wx, Wh, b = self.params
x, h_prev, h_next = self.cache
dt = dh_next * (1 - h_next ** 2)
db = np.sum(dt, axis=0)
dWh = np.dot(h_prev.T, dt)
dh_prev = np.dot(dt, Wh.T)
dWx = np.dot(x.T, dt)
dx = np.dot(dt, Wx.T)
self.grads[0][...] = dWx
self.grads[1][...] = dWh
self.grads[2][...] = db
return dx, dh_prevclass RNN: def __init__(self, Wx, Wh, b): self.params = [Wx, Wh, b] self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)] self.cache = NoneRNN을 구현하는 클래스이다.
__init__()함수는Wx,Wh,b를 인자로 입력 받는다.
Wx: 입력벡터의 가중치 행렬
Wh: 은닉벡터의 가중치 행렬
b: 편향(입력벡터 편향 + 은닉벡터 편향)
def forward(self, x, h_prev): Wx, Wh, b = self.params t = np.dot(h_prev, Wh) + np.dot(x, Wx) + b h_next = np.tanh(t)
self.cache = (x, h_prev, h_next) return h_next
def backward(self, dh_next): Wx, Wh, b = self.params x, h_prev, h_next = self.cache
dt = dh_next * (1 - h_next ** 2) db = np.sum(dt, axis=0) dWh = np.dot(h_prev.T, dt) dh_prev = np.dot(dt, Wh.T) dWx = np.dot(x.T, dt) dx = np.dot(dt, Wx.T)
self.grads[0][...] = dWx self.grads[1][...] = dWh self.grads[2][...] = db
return dx, dh_prev
TimeRNN
class TimeRNN:
def __init__(self, Wx, Wh, b, stateful=False):
self.params = [Wx, Wh, b]
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
self.layers = None
self.h, self.dh = None, None
self.stateful = stateful
def forward(self, xs):
Wx, Wh, b = self.params
N, T, D = xs.shape
D, H = Wx.shape
self.layers = []
hs = np.empty((N, T, H), dtype='f')
if not self.stateful or self.h is None:
self.h = np.zeros((N, H), dtype='f')
for t in range(T):
layer = RNN(*self.params)
self.h = layer.forward(xs[:, t, :], self.h)
hs[:, t, :] = self.h
self.layers.append(layer)
return hs
def backward(self, dhs):
Wx, Wh, b = self.params
N, T, H = dhs.shape
D, H = Wx.shape
dxs = np.empty((N, T, D), dtype='f')
dh = 0
grads = [0, 0, 0]
for t in reversed(range(T)):
layer = self.layers[t]
dx, dh = layer.backward(dhs[:, t, :] + dh)
dxs[:, t, :] = dx
for i, grad in enumerate(layer.grads):
grads[i] += grad
for i, grad in enumerate(grads):
self.grads[i][...] = grad
self.dh = dh
return dxs
def set_state(self, h):
self.h = h
def reset_state(self):
self.h = None
TimeEmbedding
class TimeEmbedding:
def __init__(self, W):
self.params = [W]
self.grads = [np.zeros_like(W)]
self.layers = None
self.W = W
def forward(self, xs):
N, T = xs.shape
V, D = self.W.shape
out = np.empty((N, T, D), dtype='f')
self.layers = []
for t in range(T):
layer = Embedding(self.W)
out[:, t, :] = layer.forward(xs[:, t])
self.layers.append(layer)
return out
def backward(self, dout):
N, T, D = dout.shape
grad = 0
for t in range(T):
layer = self.layers[t]
layer.backward(dout[:, t, :])
grad += layer.grads[0]
self.grads[0][...] = grad
return None
TimeAffine
class TimeAffine:
def __init__(self, W, b):
self.params = [W, b]
self.grads = [np.zeros_like(W), np.zeros_like(b)]
self.x = None
def forward(self, x):
N, T, D = x.shape
W, b = self.params
rx = x.reshape(N*T, -1)
out = np.dot(rx, W) + b
self.x = x
return out.reshape(N, T, -1)
def backward(self, dout):
x = self.x
N, T, D = x.shape
W, b = self.params
dout = dout.reshape(N*T, -1)
rx = x.reshape(N*T, -1)
db = np.sum(dout, axis=0)
dW = np.dot(rx.T, dout)
dx = np.dot(dout, W.T)
dx = dx.reshape(*x.shape)
self.grads[0][...] = dW
self.grads[1][...] = db
return dx