목차
- 그래프
- 그래프 순회
- DFS
- BFS
- 백트래킹
- 그래프 순회 문제
그래프
- 그래프(graph, G)
- 그래프는 노드들과 노드들을 연결하는 엣지들의 집합이다.
- G = {V, E}
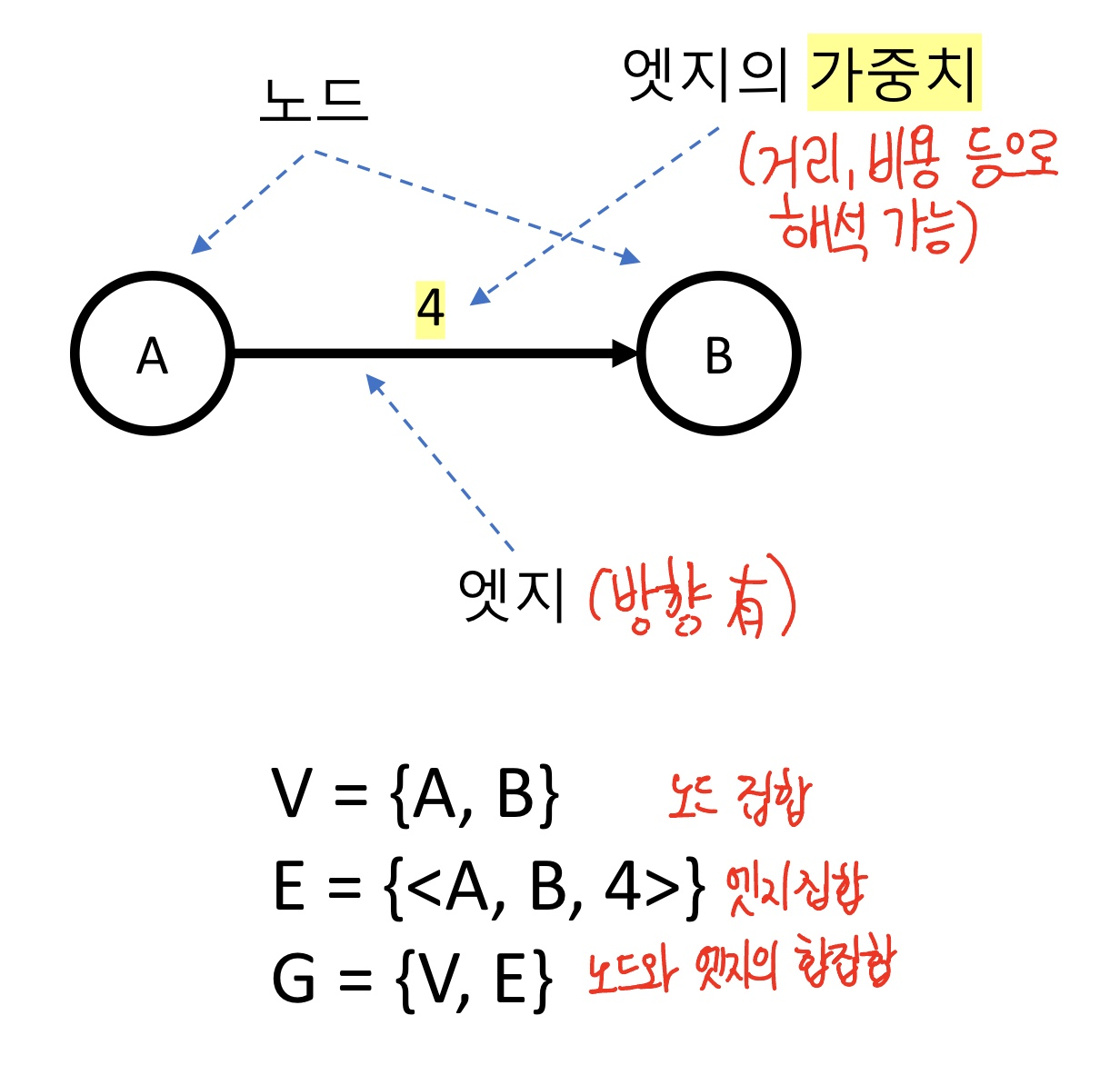
[출처: 황용득 교수님]
- 노드(node, vertex, 정점)
: 객체를 개념적으로 나타낸 것- V: 노드의 집합
- 엣지(edge, Link, 간선)
: 노드들의 관계를 개념적으로 나타낸 것- E: 엣지의 집합
- 방향을 가질 수 있음
- 가중치(= 거리, 비용)를 가질 수 있음
그래프 이론
- 그래프 이론이 사용되는 곳: 노드와 엣지의 집합!
- 인터넷 네트워크
- 지하철 노선도
- 화학 분자
- 뇌(뉴런 간 연결)
- 온톨로지
그래프 용어
- 방향 그래프(directed graph)
: 엣지에 방향이 있는 그래프- <A,B>: 노드 A에서 노드 B로 가는 간선
- 무방향 그래프(undirected graph)
: 엣지에 방향이 없는 그래프- 양 방향 모두 이동 가능
- (A,B): 노드 A와 노드 B를 연결하는 간선. A→B, B→A 모두 가능
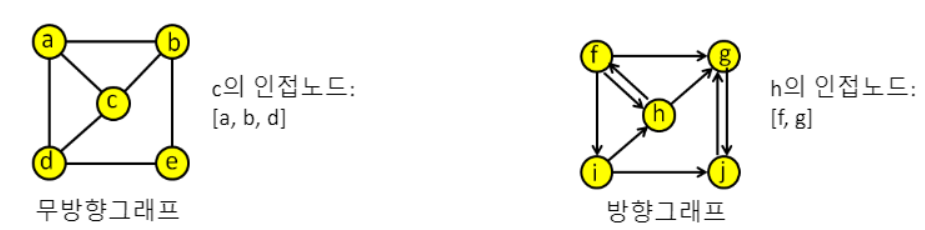
[출처: 황용득 교수님]
*인접노드: 어떤 노드 v가 있을 때, v의 인접노드는 v에서 바로 갈 수 있는 노드들의 집합
- 차수(degree)
- 무방향 그래프에서 차수는 노드에 연결된 엣지의 수
- 방향 그래프에서는 진입차수와 진출차수로 구분
1) 진입차수(in-degree): 노드로 들어오는 엣지의 수
2) 진출차수(out-degree): 노드에서 밖으로 나가는 엣지의 수
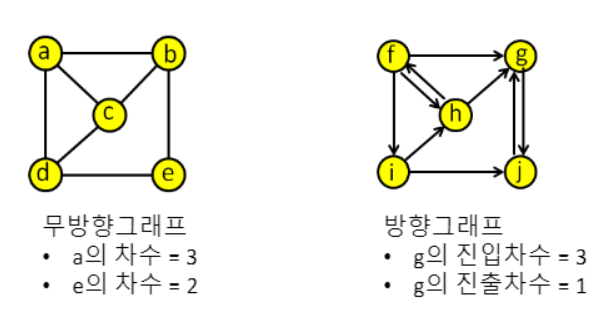
[출처: 황용득 교수님]
-
경로(path)
: 시작 노드부터 도착 노드까지 모든 노드들을 나열한 것(중복 포함)- 예) 노드 a에서 출발하여 노드 e에 도착하는 다양한 경로들
- [a,b,e]
- [a,b,a,b,e]
- [a,c,b,e]
- [a,c,d,e]
- ...
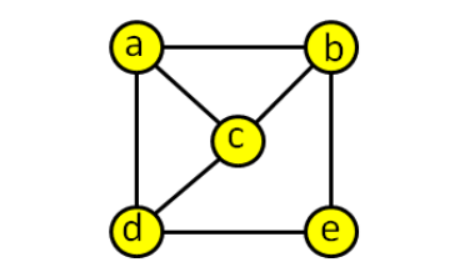
- 예) 노드 a에서 출발하여 노드 e에 도착하는 다양한 경로들
-
단순 경로(simple_path)
: 중복 제외 시작 노드부터 도착 노드까지 모든 노드들을 나열한 것- 예) 노드 a에서 출발하여 노드 e에 도착하는 다양한 경로들
- [a,b,e]
- [a,c,b,e]
- [a,c,d,e]
- ...
- 예) 노드 a에서 출발하여 노드 e에 도착하는 다양한 경로들
-
사이클(cycle)
: 시작노드와 도착노드가 같고(순환), 도착노드를 제외한 모든 노드들은 중복이 없는 경로(단순 경로) -
⭐🌲트리(tree)🎄
-
사이클 없이 모든 노드들이 연결되어있는 그래프
(트리 ⊂ 그래프)
-
그래프를 표현하는 방법(1)
- 인접 행렬(adjacency matrix)
- 행렬 형태 그래프를 표현
- 노드
i에서 노드j로 가는 엣지가 없는 경우 graph[i][j] = 0- 가중치가 있는 엣지라면 1대신 가중치 저장
- 노드
- 예시)
- 노드 1에서 노드 3으로 가는 엣지가 있다면
graph[1][3]은 1이다.
- 노드 1에서 노드 3으로 가는 엣지가 있다면
- 행렬 형태 그래프를 표현
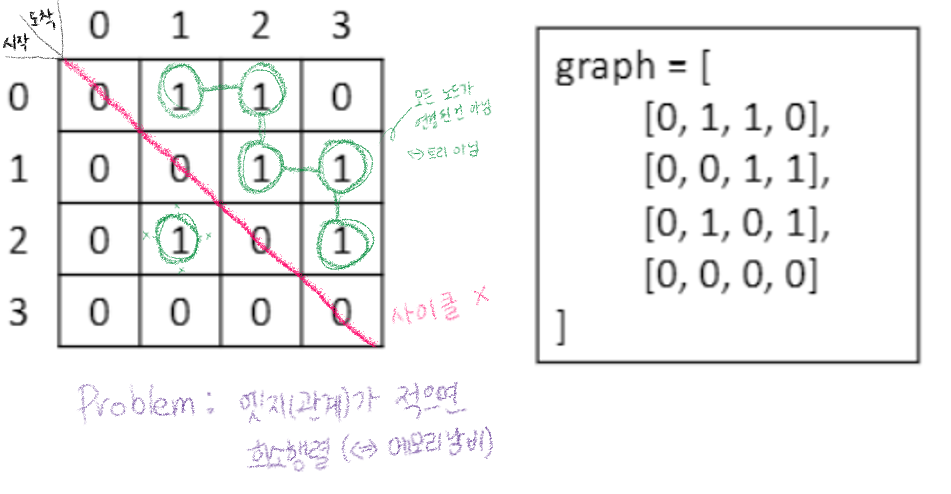
[출처: 황용득 교수님]
그래프를 표현하는 방법(2)
- 인접 리스트(adjacency list)
- 각 노드마다 인접한 노드들을 연결리스트로 저장
→ 파이썬에서 인접 리스트를 딕셔너리와 리스트로 구현 - 예시)
노드 0에서 갈 수 있는 노드는노드 1과노드 2이다.
-graph[0] = [1,2]노드 1에서 갈 수 있는 노드는노드 2와노드 3이다.graph[1] = [2,3]
노드 3에서 갈 수 있는 노드는 없다.graph[3] = []
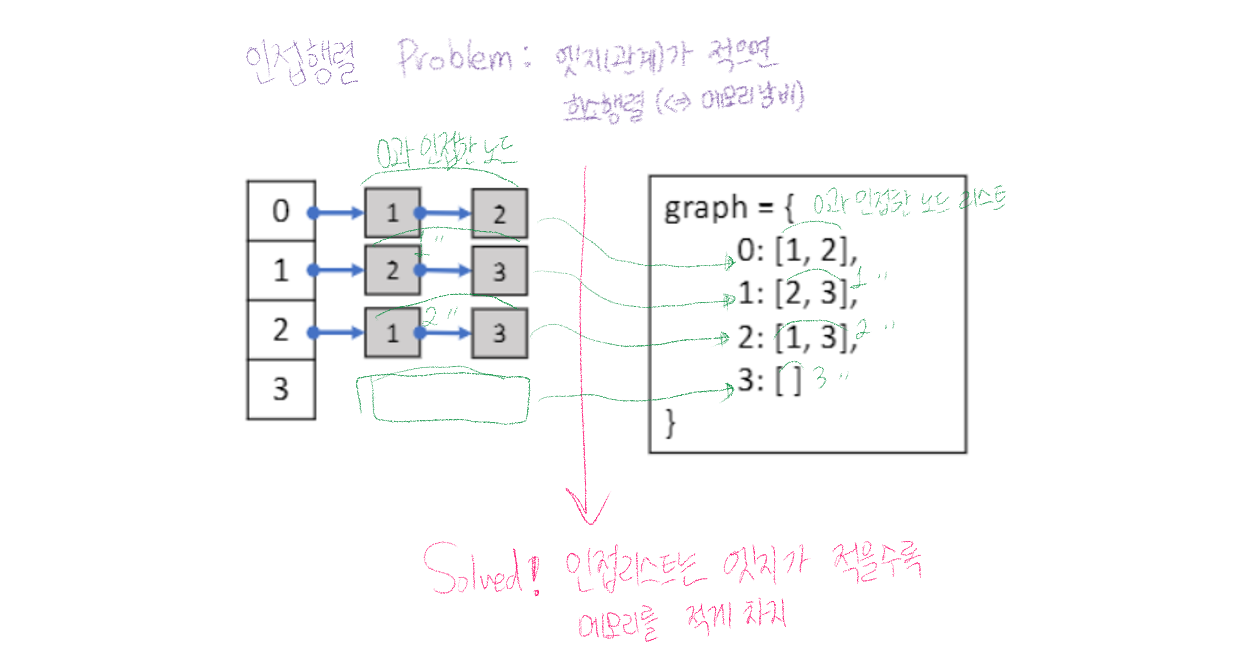
그래프 탐색(순회)
-
그래프 탐색(순회)
- 그래프에 있는 모든 노드들을 방문 탐색하는 것
-
그래프 탐색의 2가지 방법
- 깊이우선탐색(DFS, depth first search)
- 재귀함수나 스택을 사용하여 구현
- 너비우선탐색(BFS, breadth first search)
- 큐를 이용하여 구현
- 깊이우선탐색(DFS, depth first search)
-
장점
- DFS의 장점
- 빠르고 쉽게 구현 가능
- BFS의 장점
- 최단거리, 최소값 등 최적화된 경로를 찾는데 유리
- DFS의 장점
깊이우선탐색
깊이우선탐색 알고리즘
만일 노드 v(시작노드)를 방문하지 않았다면:
1) 노드 v를 방문
2) 노드 v에 인접한 모든 노드 w에 대해서, w를 깊이우선탐색 (재귀적 정의)
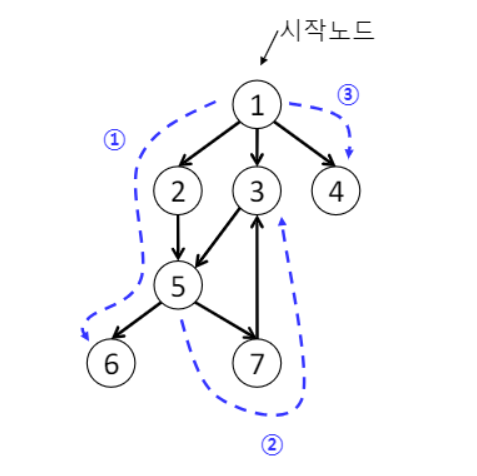
- 예시) 노드 1부터 시작
1) 1→2→5→6 방문 (인접노드 DFS 우선)
1-1) 6→5→7 (더 갈데가 없으면 자신을 호출한 이전 노드로 이동)
2) 7→3 방문
2-1) 7→5→2→1→4
3) 4 방문
⭐⭐깊이우선탐색 구현⭐⭐
graph_DFS- 그래프에서 노드들을 DFS 방법으로 방문한 결과를 리스트 형태로 리턴
- 변수들
graph: 그래프start: 시작노드visited: 딕셔너리, k노드를 방문했다면visited[k] = Trueorder: 방문한 순서대로 노드들을 저장
from typing import List, Dict, Any
def graph_DFS(graph: Dict[Any, List])-> List: # 깊이우선탐색
order = [] # 방문한 순서대로 노드 저장
visited = {k: False for k in graph} # 노드의 방문여부 저장
"""
k: 노드의 키
False: 방문 여부 초기화(모두 미방문)
"""
def dfs(start: Any)-> None: # 시작 노드와 연결된 모든 노드 방문
if not visited[start]: # 시작 노드가 미방문이라면
visited[start] = True # 방문으로 변경하고
order.append(start) # order 리스트에 추가하여 방문 순서 기록
for w in graph[start]:
# w: start에 인접한 노드
dfs(w) # 모든 노드를 다 방문
for i in graph: # 그래프의 처음 노드부터 순회
if not visited[i]: # 미방문 상태라면
dfs(i) # dfs함수로 방문 시작
return order # 방문한 순서 목록을 return
graph = {
1: [2,3,4],
2: [5],
3: [5],
4: [],
5: [6,7],
6: [],
7: [3],
}
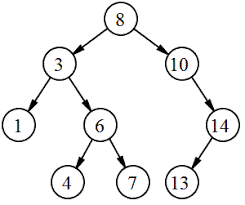
print(graph_DFS(graph))깊이우선탐색: 전위 순회
- 전위 순회: root를 먼저 방문
- 중위 순회: 왼쪽 자식 - root - 오른쪽 자식
- 후위 순회: 왼쪽 자식- 오른쪽 자식 - root
- 레벨 순회: 글을 읽는 순서로
너비우선탐색(BFS)
- 임의의 노드(보통 루트 노드)에서 시작해 인접한 노드를 먼저 탐색하는 방법
- 깊게(deep) 탐색하기 전에 넓게(wide) 탐색
- 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 적합
- DFS와 유사하지만 목적이 다름
- 너비우선탐색 알고리즘은 큐를 사용
- 너비우선탐색에서 노드를 방문하는 여러가지 방법들
- 노드를 방문하고 큐에 삽입(밥 먹고 줄 서기)
- ⭐큐에서 나온 노드를 방문
- 큐에 삽입되었다는 기록을 하고, 큐에서 나온 노드를 방문
너비우선탐색 알고리즘
- 큐에 삽입되는 순서대로 방문
- 시작노드를 큐에 삽입
- 큐가 비어있지 않다면
- 디큐하여 노드 v를 꺼낸다.
- v를 방문하지 않았다면,
- v를 방문
- v에 인접한 모든 노드 w를 큐에 삽입
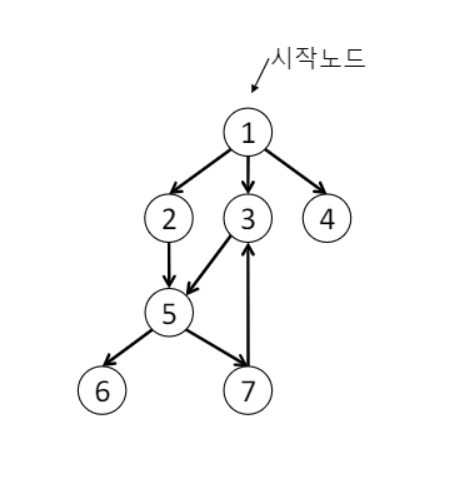
- 예시) 노드 1부터 시작
- 1→2→3→4→5→6→7 방문
- 1
- 2→3→4: 시작노드에서 한 칸
- 5: 시작노드에서 두 칸
- 6→7: 시작노드에서 세 칸
- 1→2→3→4→5→6→7 방문
너비우선탐색 구현
graph_BFS- 모든 노드를 방문하는 것이 목적(단, 시작 노드에서 갈 수 있는 노드들만)
- 그래프에서 노드들을 BFS방법으로 방문한 결과를 리스트 형태로 리턴
- 변수들
graph: 그래프start: 시작노드visited: 딕셔너리, k 노드를 방문했다면visited[k] = Trueorder: 방문한 순서대로 노드들을 저장
from typing import List, Dict, Any
def graph_DFS(graph: Dict[Any, List])-> List:
order = [] # 방문한 순서대로 노드 저장
visited = {k: False for k in graph} # 노드의 방문여부 저장
def dfs(start: Any)-> None:
if not visited[start]:
visited[start] = True # 방문
order.append(start) # 방문 순서 기록
for w in graph[start]:
# w: start에 인접한 노드
dfs(w)
for i in graph:
if not visited[i]:
dfs(i)
return order
graph = {
1: [2,3,4],
2: [5],
3: [5],
4: [],
5: [6,7],
6: [],
7: [3],
}
print(graph_DFS(graph))백트래킹 알고리즘
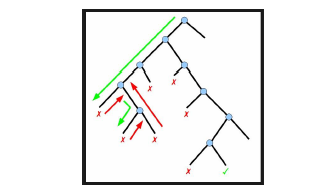
- 그래프나 트리를 탐색할 때, 경우의 수를 줄이기 위해 사용하는 방법
- 특정 노드가 유망하다면 → 노드 탐색
- 특정 노드가 유망하지 않다면 → 이전 노드(부모 노드)로 돌아감
# 백트래킹 알고리즘 빈 깡통 코드 1(우리 pick)
def checknode(v): # 백트래킹
if promising(v): # 유망한지
if is_solution(v): # 정답이라면
print("Solution:", v) # 정답 출력
else: # 오답이라면
for w in children(v): # w가 v의 자식이라면
checknode(w) # 재귀 백트래킹
def promising(v):
# Example logic: check if node 'v' does not violate constraints
# This is problem-specific and needs to be adapted
return True # Replace with actual logic
def is_solution(v):
# Example logic: check if node 'v' meets the goal criteria
# This is problem-specific and needs to be adapted
return False # Replace with actual logic
def children(v):
# Example logic: generate the next set of nodes from 'v'
# This is problem-specific and needs to be adapted
return [] # Replace with actual logic# 백트래킹 알고리즘 빈 깡통 코드 2(가끔 쓰임)
def checknode(v): # 백트래킹 코드, v가 유망하다고 가정
if is_solution(v): # v가 답이라면
print(v) # v 출력
else: # v가 답이 아니라면
for w in children(v): # w가 v의 자식이라면
if promising(w): # w가 유망하다면
checknode(w) # 백트래킹 재귀호출실전 문제(섬의 개수)
- Q. 1을 육지로, 0을 물로 가정한 2D 그리드 맵이 주어졌을 때, 섬의 개수를 계산하여라
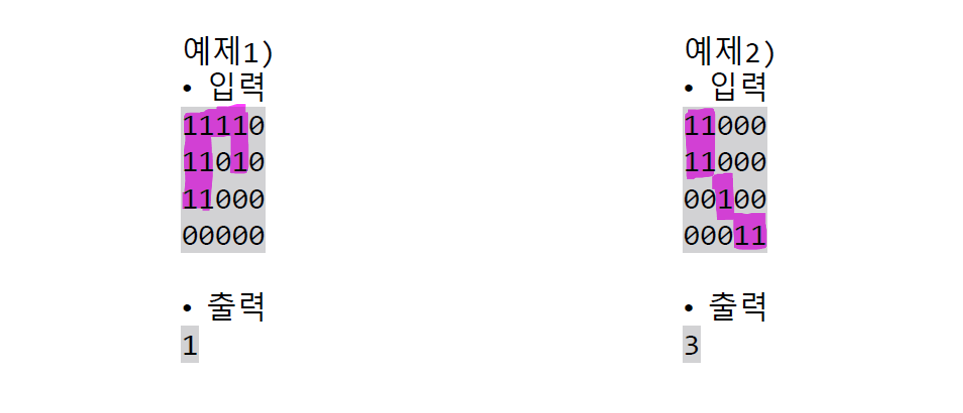
[출처: 황용득 교수님]
- 그리드 맵을 표현하는 방법
- 2차원 리스트 이용
- 각 노드들이 동서남북으로 연결된그래프라고 가정한다.

[출처: 황용득 교수님]
- 인접행렬이 아니고 Grid Map이다.(직사각형이고 대각선이 0이 아님)
실전 문제(미로 찾기)
섬의 개수 구하는 방법
1. 시작 노드와 연결된 모든 노드(동서남북)들에 탐색 가능한 경우 깊이우선탐색을 한다. 단, 한 번 방문한 노드는 다시 방문하지 않는다.
- 탐색을 했다면 섬의 개수를 1 증가시킨다.
- 현재 노드가 탐색 가능한 경우인지 확인
- 현재 노드가 탐색 가능하다면 promising(유망한)하다 한다.
- promising 여부 확인 방법
- 노드가 grid 맵 안에 존재해야함
- 노드가 방문된 적이 없어야 함
- 노드가 육지여야함
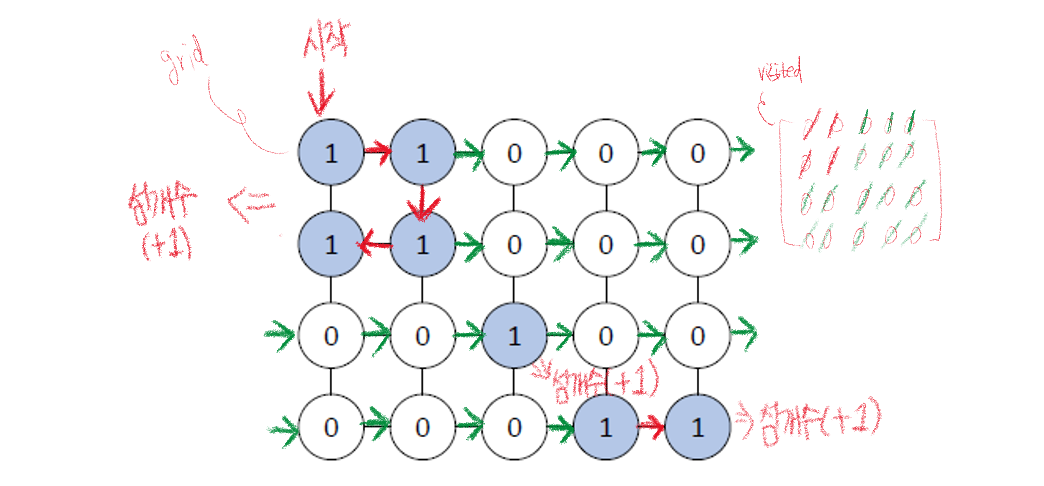
[출처: 황용득 교수님]
섬의 개수 문제 풀이 1
is_promising(row, col)row와col이grid범위 안에 있고,grid[row][col]을 방문한 적이 없고, 육지인 경우True리턴row: 행 인덱스col: 열 인덱스
dfs(row, col): (row, col)위치에서 연결된 모든 육지를 방문한다.
from typing import List, Dict, Any
def counting_islands(grid: List[List[int]])-> int:
n_rows = len(grid) # 줄 개수
n_cols = len(grid[0]) # 컬럼 수
visited = [[False] * n_cols for _ in range(n_rows)]
def is_promising(row: int, col: int)-> bool:
"""grid[row][col]이 유망한지 확인"""
if 0 <= row < n_rows and 0 <= col < n_cols and \
grid[row][col] == 1 and not visited[row][col]:
return True
else:
return False
def dfs(row: int, col: int)-> None:
"""grid[row][col]을 깊이우선탐색"""
if is_promising(row, col):
visited[row][col] = True # 방문했음
dfs(row, col + 1) # 동
dfs(row, col - 1) # 서
dfs(row + 1, col) # 남
dfs(row - 1, col) # 북
count = 0 # 섬의 수
# 모든 노드를 깊이우선탐색
for i in range(n_rows):
for j in range(n_cols):
if is_promising(i,j):
dfs(i, j)
count += 1
return count섬의 개수 문제 해결 방법 2: 너비우선탐색
from typing import List, Dict, Any
from collections import deque
def counting_islands_bfs(grid: List[List[int]])->int:
n_rows = len(grid)
n_cols = len(gird[0])
visited = [[False]*n_cols for _ in range(n_Rows)]
def is_promising(row: int, col: int)-> bool:
"""grid[row][col]이 유망한지 확인"""
if 0 <= row < n_rows and 0 <= col <n_cols and \
grid[row][col] == 1 and not visited[row][col]:
return True
else:
return False
def bfs(row: int, col: int)-> None:
"""grid[row][col]을 너비우선탐색"""
queue = deque()
queue.append((row, col))
while queue:
i, j = queue.popleft()
if is_promising(i, j):
visited[i][j] = True
queue.append((i, j+1)) # 동
queue.append((i, j-1)) # 서
queue.append((i+1, j)) # 남
queue.append((i-1, j)) # 북
count = 0
# 모든 노드를 너비우선탐색
for i in range(n_rows):
for j in range(n_cols):
if is_promising(i, j):
bfs(i, j)
count += 1
return count실전 문제(미로 찾기)
- Q. 1은 지나갈 수 있고 0을 벽으로 가정한 2D 그리드 맵이 주어졌을 떄, 좌측상단에서 출발하여 우측하단으로 이동할 때 지나야 하는 최소의 칸의 수를 구하시오.
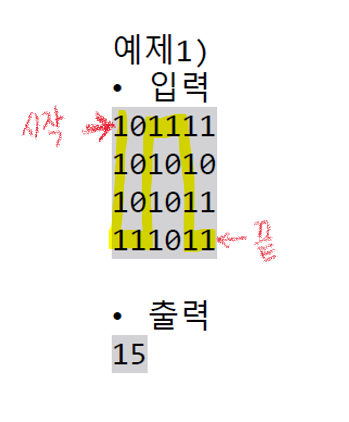
미로 찾기 문제 해결 방법
from typing import List, Tuple, Dict, Any
from collections import deque
def miro(grid: List[List])-> int:
n_rows = len(grid)
n_cols = len(grid[0])
visited = [[0] * n_cols for _ in range(n_rows)] # 지나간 칸 수를 저장
start_pos = (0, 0) # 시작 위치
target_pos = (n_rows - 1, n_cols - 1) # 목표 위치
visited[0][0] = 1 # 시작 위치는 이미 지났다.
dxdy = [(0,1), (0,-1), (1, 0), (-1, 0)] # 동서남북 방향
queue = deque()
def is_promising(row: int, col: int)-> bool:
"""grid[row][col]이 유망한 지 확인"""
if 0 <= row < n_rows and 0 <= col < n_col and \
grid[row][col] == 1 and visited[row][col] == 0:
return True
else:
return False
queue.append(start_pos)
while queue:
x, y = queue.popleft()
if (x, y) == target_pos: # 목표 도착
return visited[x][y]
for dx, dy in dxdy:
(nx, ny) = (x+dx, y+dy)
if is_promising(nx, ny):
visited[nx][ny] = visited[x][y] + 1 # 현재값 + 1 = 다음 위치에ㅣㅆ는 노드의 수
queue.append((nx, ny))
return -1 # 목표까지 가지 함실전 문제(최대 섬의 크기 출력)
from typing import Any
def max_island_size(grid: list[list[int]]) -> int:
n_rows = len(grid)
n_cols = len(grid[0])
visited = [[False]*n_cols for _ in range(n_rows)]
def is_promising(row: int, col: int)-> bool:
"""grid[row][col]이 유망한 지 확인"""
if 0 <= row < n_rows and 0 <= col < n_cols and \
grid[row][col] == 1 and visited[row][col] == 0:
return True
else:
return False
def dfs(row: int, col: int)-> None:
"""grid[row][col]을 깊이우선탐색"""
if is_promising(row, col):
visited[row][col] = True # 방문했음
dfs(row, col + 1) # 동
dfs(row, col - 1) # 서
dfs(row + 1, col) # 남
dfs(row - 1, col) # 북
sizes = []
isl_size = 0
# 모든 노드를 깊이우선탐색
for i in range(n_rows):
for j in range(n_cols):
if is_promising(i,j):
isl_size += 1
sizes.append(isl_size)
dfs(i, j)
return max(sizes)
# 아래는 수정하지 마시오.
grid = [
[1,1,0,0,0],
[1,1,0,0,0],
[0,0,1,0,0],
[0,0,0,1,1],
]
print(max_island_size(grid))
grid = [
[1,1,0,0,1],
[1,1,0,0,0],
[0,0,1,1,1],
[0,0,0,1,1],
]
print(max_island_size(grid))