목차
- 정렬
- 정렬 안정성
- 비교 정렬
- 선택 정렬
- 삽입 정렬
- 합병 정렬
- 퀵 정렬
정렬
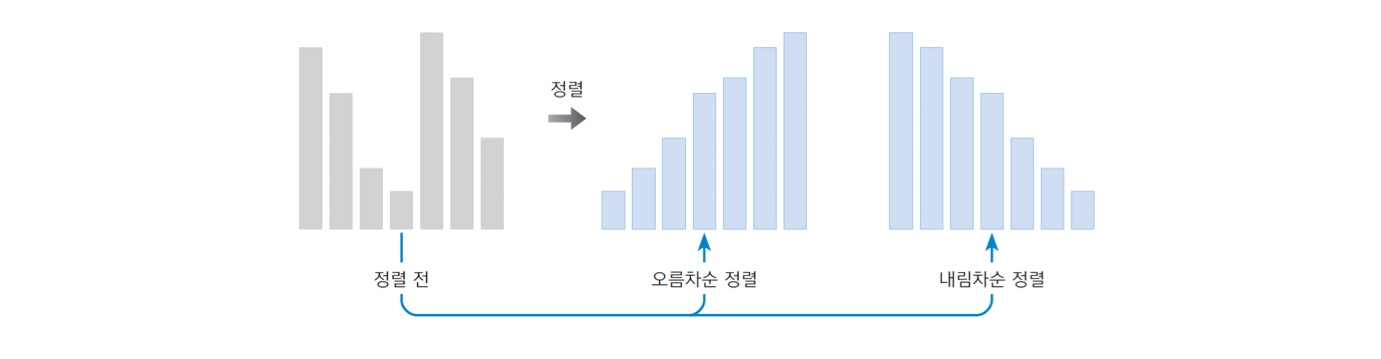
- 정렬(sorting): 대소 비교를 통해 데이터 집합을 순서대로 나열하는 작업
- 오름차순 정렬: 값이 작은 데이터가 앞쪽에 오는 순서로 정렬
- 내림차순 정렬: 값이 큰 데이터가 앞쪽에 오는 순서로 정렬
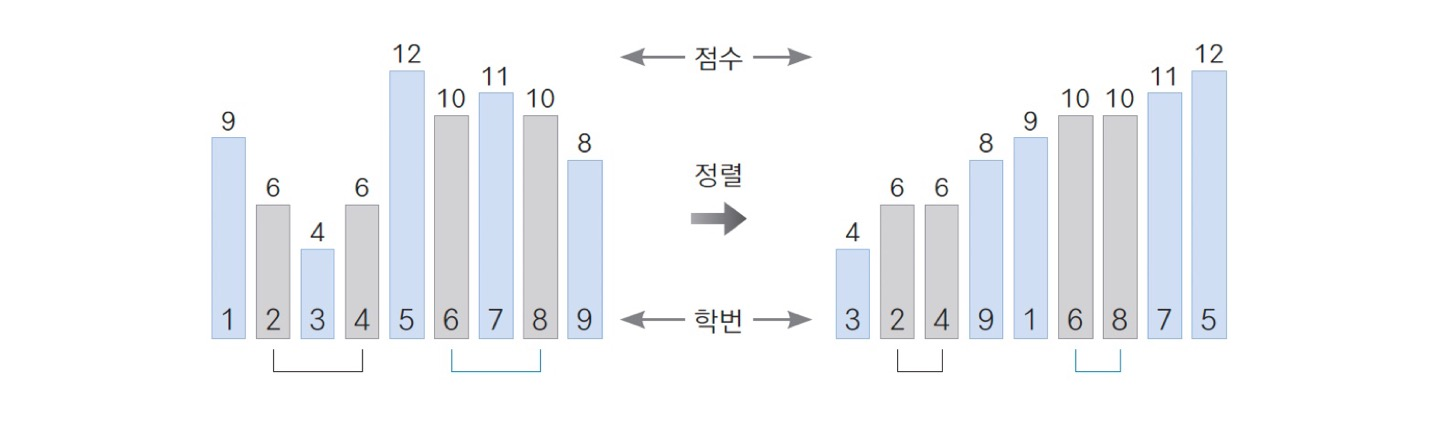
- 안정적인 정렬(stable sort): 키값이 같을 때 정렬 이전의 순서가 유지되는 정렬
선택 정렬
- 선택 정렬(selection sort)
- 인간에게 가장 자연스러운 정렬
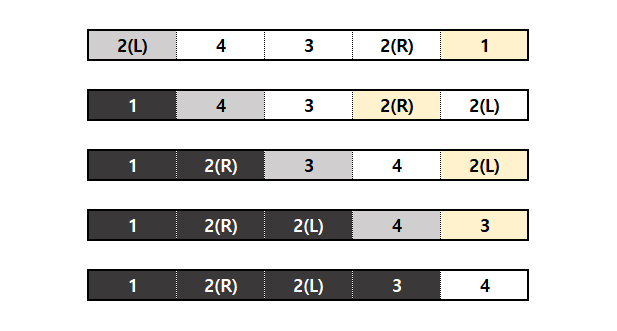
- 가장 작은 원소부터 알맞은 위치로 옮기는 작업을 반복하여 정렬
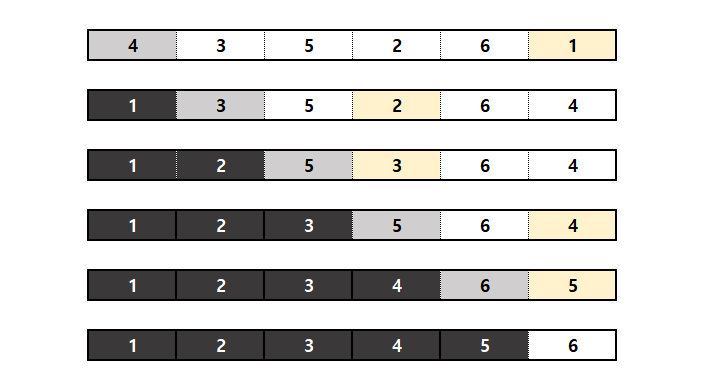
- 선택 정렬 과정
1) 아직 정렬하지 않은 부분에서 값이 가장 작은 원소 선택
2) 1)에서 찾은 가장 작은 원소와 아직 정렬하지 않은 부분에서 맨 앞에 있는 원소 교환
3) 정렬 안된 부분이 사라질 때까지 반복
선택 정렬 구현
def selection_sort(seq: list)-> None:
"""선택 정렬"""
n = len(seq)
for i in range(n-1):
# i: 정렬 안 된 부분에서 맨 앞 원소 인덱스
# min_idx: # 정렬 안 된 부분에서 가장 작은 원소 인덱스
min_idx = i # 초기화
for j in range(i+1, n):
# j: 최소값을 찾기 위해서 탐색 중인 인덱스
if seq[j] < seq[min_idx]:
min_idx = j # min_idx 업데이트
# i와 min_idx의 원소를 교환
seq[i], seq[min_idx] = seq[min_idx], seq[i]
arr = [6,4,8,3,1,9,7]
selection_sort(arr)
print(arr)선택 정렬 특징
- 시간복잡도
- 최선: O()
- 평균: O()
- 최악: O()
최선의 경우: 이미 정렬되어있는 배열을 선택 정렬 시, 정렬 안 된 부분에서 최솟값 찾기 + 무조건 교환
O(N+(N-1)+(N-2)+...+1) + O(1+1+...+1) = O((1+N)N/2) + O(N) = O()
평균 경우: 무작위로 섞여있는 배열을 선택 정렬 시, 이미 정렬되어있는 배열을 선택 정렬 시, 정렬 안 된 부분에서 최솟값 찾기 무조건 교환
O(N+(N-1)+(N-2)+...+1) + O(1+1+...+1) = O((1+N)N/2) + O(N) = O()
최악의 경우: 역순으로 정렬되어있는 배열을 선택 정렬 시, 이미 정렬되어있는 배열을 선택 정렬 시, 정렬 안 된 부분에서 최솟값 찾기 무조건 교환
O(N+(N-1)+(N-2)+...+1) + O(1+1+...+1) = O((1+N)N/2) + O(N) = O()
- 장점
- 비교 정렬 알고리즘들 중에서 교환 횟수가 가장 적음(항상 N번) - 단점
- 불안정 정렬
-키 값이 같은 원소들의 순서가 정렬 후 바뀌기도 함
- 불안정 정렬
- 낮은 효율성으로 거의 사용되지 않음
삽입 정렬
-
아주 유용함
-
삽입 정렬(insertion sort)
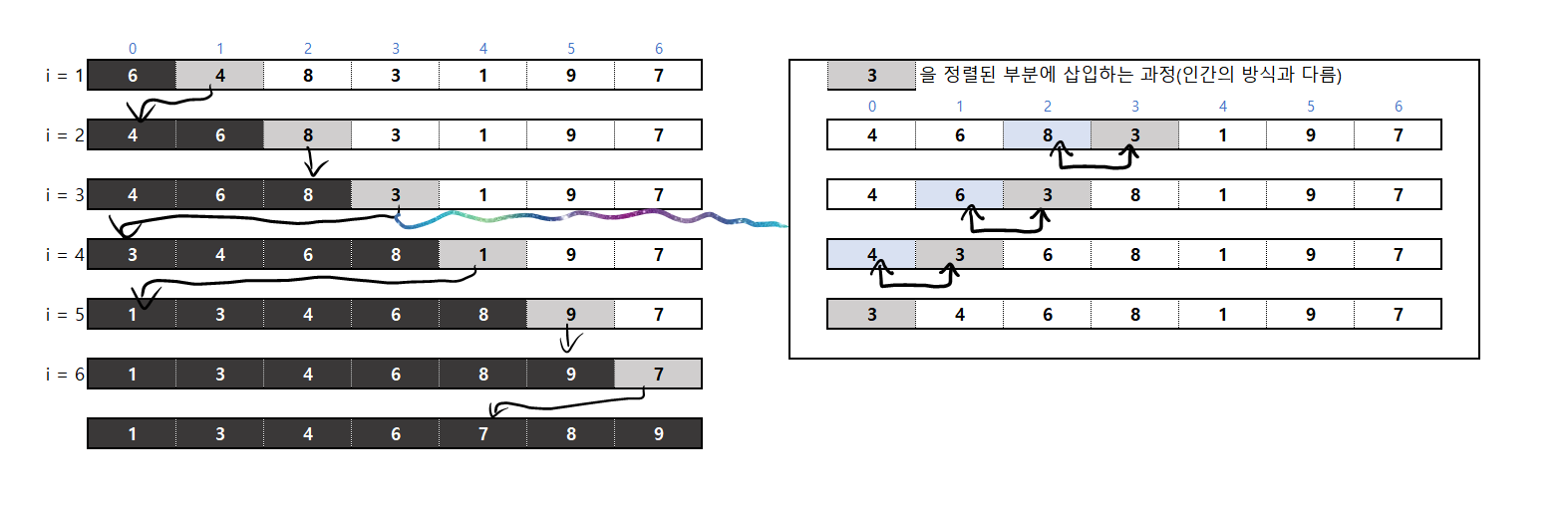
- 정렬 안 된 부분에서 맨 앞 원소를 정렬된 부분에 삽입해서 정렬하는 알고리즘
-
선택정렬과의 차이점
- 선택정렬은 가장 작은 원소를 선택하지만, 삽입정렬은 이 과정이 없음
-
삽입 정렬 과정
1) 아직 정렬되지 않은 부분의 맨 앞 원소를 정렬된 부분의 알맞은 위치에 삽입
삽입 정렬 구현
def insertion_sort(seq: list)-> None:
"""삽입 정렬"""
n = len(seq)
for i in range(1,n): # 0일때는 고려할 필요 없음
# (첫 원소는 부분적으로는 이미 정렬되어있다 정의하기 때문)
# i: 정렬 안 된 부분에서 맨 앞 원소의 인덱스
for j in range(i, 0, -1):
# j: 삽입할 데이터의 현재 인덱스
if seq[j-1] > seq[j]:
seq[k-1], seq[j] = seq[j], seq[j-1]
else:
break삽입 정렬 특징
- 시간복잡도
- 최선: O()
- 평균: O()
- 최악: O()
최선의 경우: 이미 정렬되어 있는 배열을 삽입 정렬할 때, 한 번씩만 비교하면 되므로 비교(O()) + 삽입 (O()) = O()이 된다.
평균 경우: 무작위로 섞여있는 배열을 삽입 정렬할 때,
최악 경우: 역순으로 정렬된 배열을 삽입 정렬할 때,
- 장점
- 안정 정렬
- 입력이 거의 정렬된 경우 우수한 성능을 보임
(정렬이 되어있으면 이동이 없기 때문)
(반대로 선택정렬은 무조건 이동이 있음) - 입력의 크기가 작은 경우(대략 20개 이하)에 매우 우수한 성능을 보임
- 삽입 정렬은 다른 정렬들과 결합하여 성능향상에 도움을 줌
- 단점
- 입력의 크기가 클 때 비효율적(평균, 최악 경우 O()
합병 정렬
- 합병 정렬(merge sort, 병합 정렬)
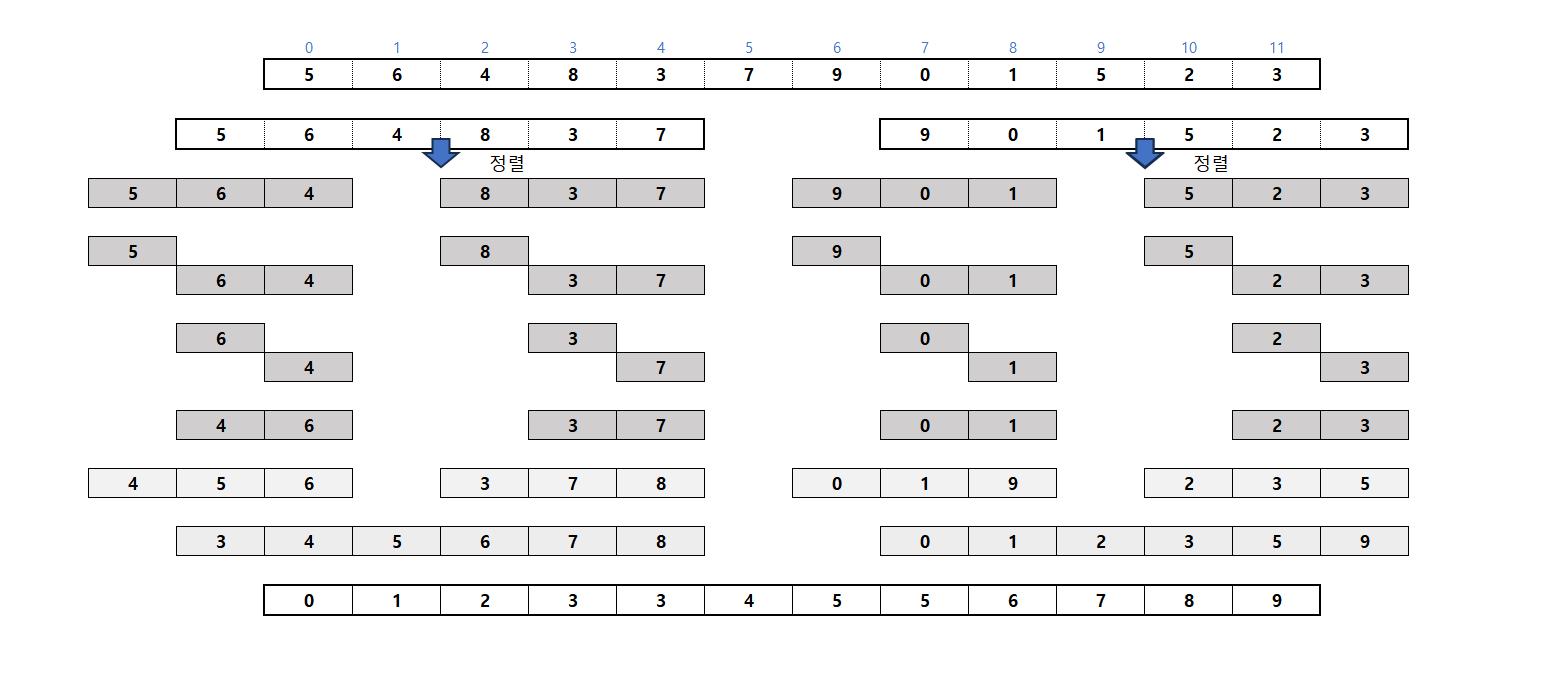
- 분할 정복 방법을 사용하여 리스트를 2개로 분할하고 각각을 재귀적으로 합병정렬한 후 정렬된 부분을 합병하는 정렬 알고리즘
- 합병 정렬 과정
1) 분할 정렬되지 않은 리스트를 절반으로 잘라 두 개의 리스트로 나눈다.
2) 정복: 각 부분 리스트를 재귀적으로 합병 정렬한다.
3) 합병: 두 부분 리스트를 다시 정렬된 하나의 리스트로 합병한다. 이 때 추가적으로 메모리가 필요하다.
분할 시간복잡도가 O()인 이유
각 분할 단계에서 배열을 반으로 나누므로 분할 단계의 수는 로그에 비례한다. 이진 분할이기 때문에, 배열의 크기가 일 때 분할 단계의 수는 이 된다.
예를 들어, 배열의 크기가 8일 때 분할 단계는 3번입니다. (8 -> 4 -> 2 -> 1) 따라서 크기가 인 배열을 분할하려면 단계가 필요하며, 각 단계에서는 배열을 반으로 나누기 때문에 이 단계들의 합이 O()이 된다.
예를 들어, 배열의 크기가 8일 때 분할 단계는 3번입니다. (8 -> 4 -> 2 -> 1) 따라서 크기가 N인 배열을 분할하려면 log₂(N) 단계가 필요하며, 각 단계에서는 배열을 반으로 나누기 때문에 이 단계들의 합이 O(log N)이 됩니다.
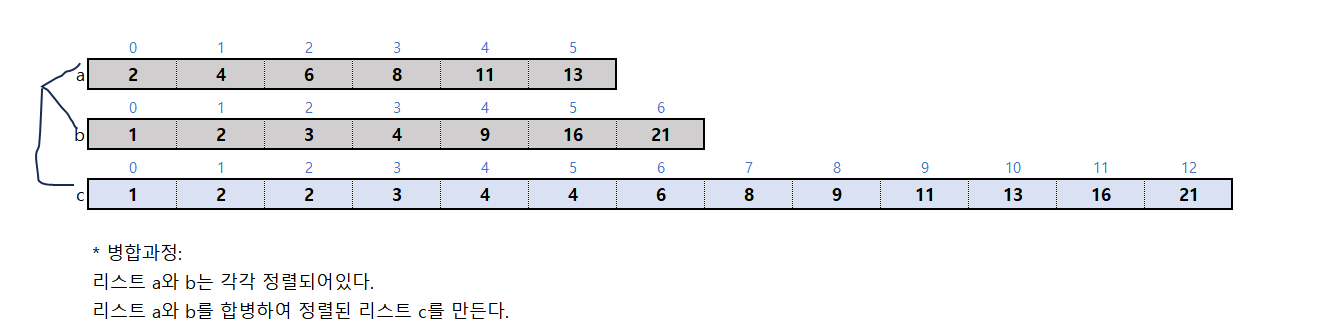
- 합병(merge)
- 각각 정렬된 2개의 리스트를 합쳐서 정렬된 하나의 리스트를 만드는 과정
- 합병 과정은 추가 메모리(O())가 필요하다.
합병 정렬 구현
- 합병 함수 구현(O())
left: 정렬된 왼쪽 리스트right: 정렬된 오른쪽 리스트result: 합병된 결과
def merge(left: list, right: list)-> list:
"""합병"""
result = [None] * (len(left) + len(right)) # 최종 결과 초기화
i = 0 # 왼쪽 리스트 인덱스 초기화
j = 0 # 오른쪽 리스트 인덱스 초기화
for k in range(len(result)): # 최종 결과에 값 채우기
if i < len(left) and j < len(right):
# 오/왼 리스트 모두 정렬할 원소가 남은 경우
if left[i] <= right[j]: # left[i]가 right[j]보다 작거나 같은 경우(안정 정렬)
result[k] = left[i] # result 리스트에 더 작은 쪽 채우기
i += 1 # 인덱스 하나 오른쪽으로 이동
else: # right[j]가 left[i]보다 작으면
result[k] = right[j] # result 리스트에 더 작은 쪽 채우기
j += 1 # 오른쪽리스트 인덱스 하나 오른쪽으로 이동
elif i >= len(left): # 왼쪽리스트 원소 모두 정렬(선택)됐다면
result[k] = right[j] # 무조건 오른쪽 리스트 원소 넣기
j += 1 # 오른쪽리스트 인덱스 하나 오른쪽으로 이동
elif j >= len(right): # 오른쪽리스트 원소 모두 정렬(선택)됐다면
result[k] = left[j] # 무조건 왼쪽 리스트 원소 넣기
i += 1 # 왼쪽리스트 인덱스 하나 오른쪽 이동
return result # 정렬된 리스트(오/왼 합쳐진) 리턴
print(merge([1,4,6],[2,5,7]))
배열의 원소 수가 1개 이하인 경우
1. 이미 정렬되어있음
배열의 원소 수가 2개 이상인 경우
1. 배열의 앞부분을 합병정렬로 정렬
2 .배열의 뒷부분을 합병정렬로 정렬
3. 배열의 앞부분과 뒷부분을 합병 후 복사
def merge_sort(seq: list)-> None:
"""합병 정렬"""
if len(seq) <= 1: # 원소가 하나 이하이면
return # 이미 정렬되어있다고 생각함, 리턴값 없고 동작만 수행
## 분할
mid = len(seq) // 2 몫(예: 총 길이가 9이면 4:5로 나뉨)
left = seq[:mid] # 0부터 mid-1까지
right = seq[mid:] # mid부터 끝까지
## 정복(재귀적 합병정렬)
merge_sort(left) # left를 합병정렬
merge_sort(right) # right를 합병정렬
## 합병
merged = merge(left, right) # left, right를 합병하여 result 리턴
for i in range(len(seq)):
seq[i] = merged[i] # 리턴 대신 seq자체 값을 정렬된 값으로 바꿈
# (얕은 복사기 때문에 원소 단위로 접근해서 변경 가능
# 단, 통으로는 불가능 seq = merged와 같이 한번에 못 바꿈)
arr = [1,5,2,6,7,2,4,8,9,4,5,3,1]
merge_sort(arr)
print(arr)합병 정렬 특징
- 시간 복잡도
- 최악: O() = 분할(O()) * 병합(O())
- 평균: O() = 분할(O()) * 병합(O())
- 최선: O() = 분할(O()) * 병합(O())
- 장점
- 입력에 상관없이 O() 시간복잡도
- 안정 정렬
- 단점
- 추가 메모리 O() 필요
- 추가적 성능향상 방법
- 크기가 작은 합병정렬은 삽입정렬(O())로 대체 => 현대 알고리즘의 정렬방식(혼합)
퀵 정렬
- 퀵 정렬(quick sort)
- 평균 경우 가장 압도적으로 빠름
- 분할 정복 방법으로 피벗(pivot) 위치를 결정하는 정렬 알고리즘
- 굉장히 빠른 정렬
퀵 정렬 과정
1. 하나의 원소를 골라서 피벗이라고 한다.
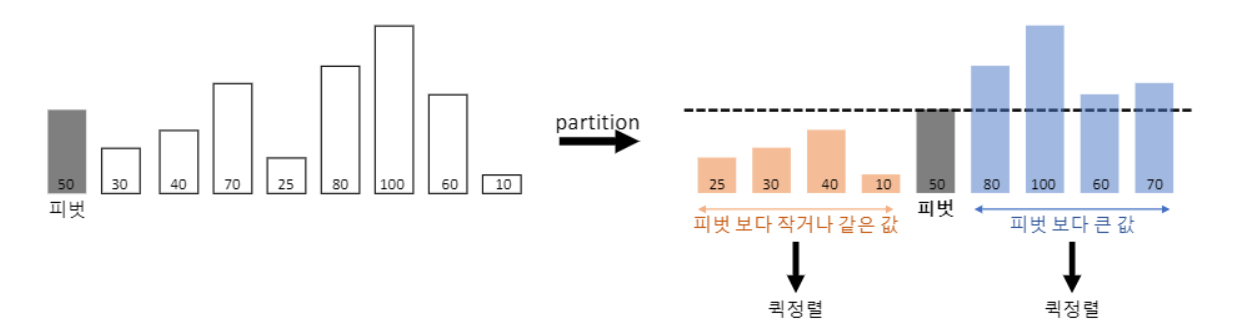
2. 피벗을 기준으로 전체 데이터를 분할(partition)한다.
- 왼쪽에는 피벗보다 작거나 같은 원소가 오고,
- 오른쪽에는 피벗보다 큰 값이 오도록 한다.
3. 분할된 작은 리스트에 대해 재귀적으로 이 과정을 반복한다.
퀵 정렬 구조
- 퀵 정렬 알고리즘
- 피벗을 정렬한다.(partition)
- 피벗의 왼쪽파트를 퀵 정렬한다.
- 피벗의 오른쪽파트를 퀵 정렬한다.
퀵 정렬 구현
def quick_sort(seq: list)-> None:
"""퀵 정렬"""
def partition(start: int, end = int)-> int:
"""피벗의 인덱스 리턴"""
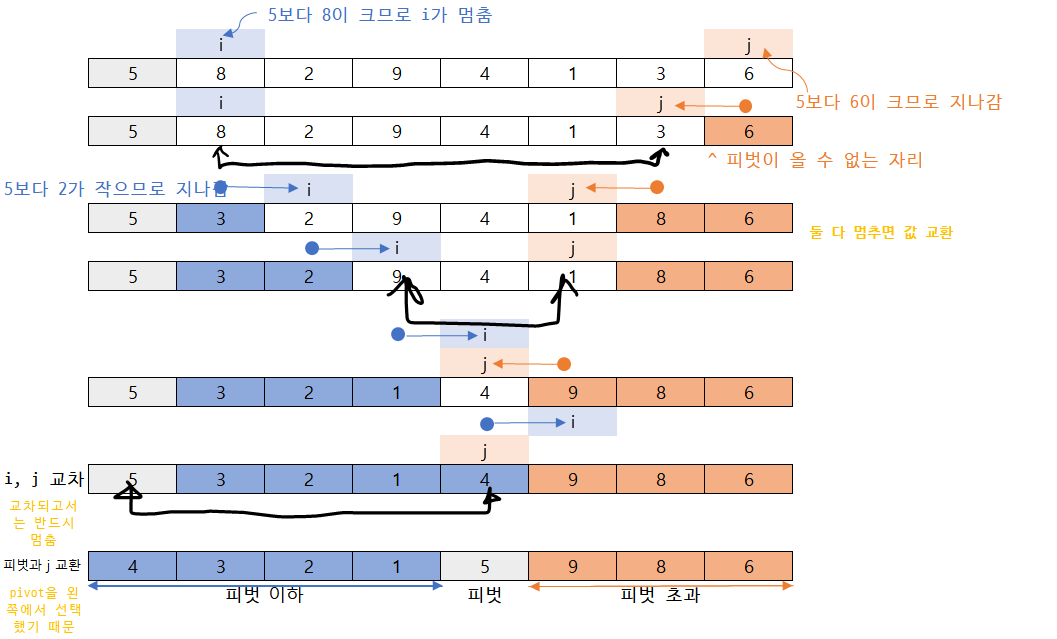
i = start + 1 # 피벗보다 작은 수를 지나치고, 큰 수에선 멈추는 애, 피벗 하나 뒤에서 시작한다.
j = end # 피벗보다 큰 수는 지나치고, 작은 수에선 멈추는 애. 배열 가장 끝에서 시작한다.
pivot = start # 여기서는 피벗으로 가장 왼쪽에 있는 노드를 선택했다.
while True: # 무한 루프
while i <= end and seq[i] <= seq[pivot]:
# i가 위치한 노드의 값이 피벗의 값보다 작거나 같으면
i += 1 # i가 한 칸 이동한다.
if i > j: # i와 j가 교차하면
seq[pivot], seq[j] = seq[j], seq[pivot] # j, 피벗 교환
break
seq[i], seq[j] = seq[j], seq[i] # i, j 교환
return j # 피벗 인덱스 리턴
def sort(start: int, end: int)-> None: # 실질적 퀵 정렬 구현
if start < end: # 정렬할 데이터가 남아있을 때
pivot = partition(start, end) # pivot 정하기
sort(start, pivot - 1) # 정렬할 데이터가 하나 줄어 빠른 검색 가능
sort(pivot + 1, end) # 재귀 호출
sort(0, len(seq) - 1) # 정렬 수행퀵 정렬 특징
-
시간복잡도
- 최선: O() = 피벗을 기준으로 오/왼 배열로 각 원소를 보내는 작업(O()) * 재귀적으로 퀵정렬을 호출하는 횟수(O())
- 항상 중간값을 선택하는 경우

- 평균: O() = 피벗을 기준으로 오/왼 배열로 각 원소를 보내는 작업(O()) * 재귀적으로 퀵정렬을 호출하는 횟수(O())
- 무작위 배열에서 피벗은 평균적으로 배열을 균등하게 나눌 수 있음

- 최악: O() = 피벗을 기준으로 오/왼 배열로 각 원소를 보내는 작업(O()) * 배열이 균등하게 안 나눠지면 거의 N번에 가깝게 피벗을 선택하고 정렬하는 작업을 반복하게 됨(O())
- 피벗이 매번(왼쪽for All) 가장 작거나 가장 클 경우 데이터 분할이 잘 안됨

-
장점
- 평균적인 경우에 매우 우수한 성능(빠르고)
- 보조 메모리를 사용하지 않음(싸다)
-
단점
- 최악의 경우 O() 시간복잡도
- 불안정 정렬
-
성능 향상 방법
- 입력의 크기가 작을 때 삽입정렬로 대체
- 피벗을 정하는 방법 개선
비교(교환) 정렬 특징
비교 정렬
- 원소들 간의 비교를 기반으로 한 정렬
- 버블, 선택, 삽입, 퀵, 합병, 힙, ...
비교 정렬이 아닌 정렬
- 기수 정렬
- 자릿수 별로 개수를 세는 것을 기반으로 정렬하는 알고리즘
비교 정렬의 특징
- 최소 비교 횟수가 Ω()임이 증명되었다.
- 어떠한 정렬 알고리즘이라도 최소 Ω()만큼의 원소 비교를 수행하지 않으면 알고리즘의 결과가 항상 정렬되어있다는 보장을 할 수 없다는 의미
정렬 알고리즘 실행 속도 측정
[출처: 황용득 교수님]
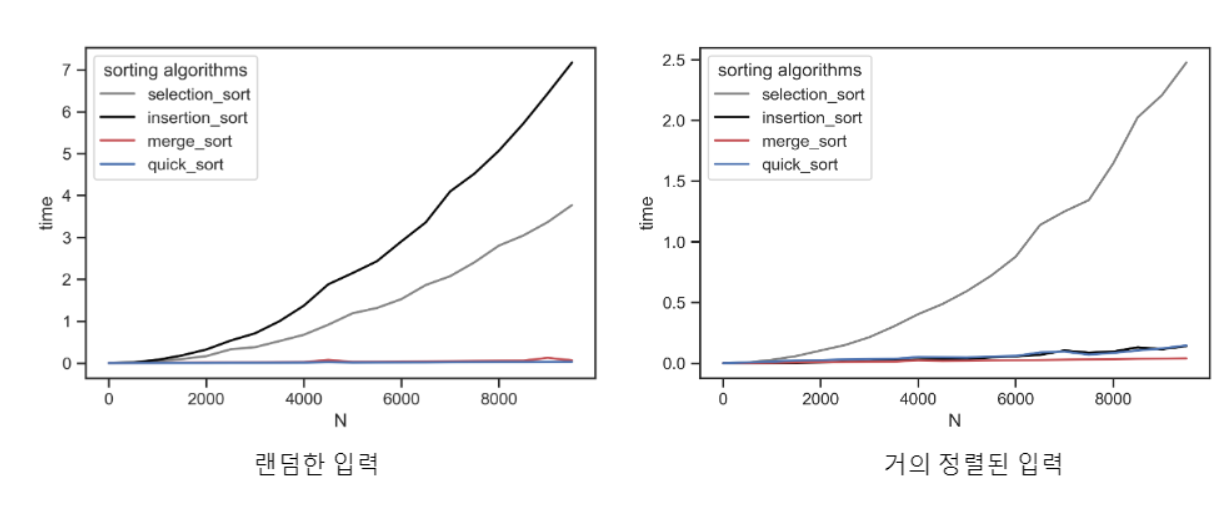
- 랜덤한 입력(평균 경우)에서의 수행 속도 비교
- 퀵 정렬 > 합병 정렬 > 선택정렬 > 삽입정렬
- 처음 20개까지는 삽입정렬이 더 빠름
- 거의 정렬된 입력(최선 경우)에서의 수행 속도 비교
- 합병 정렬 > 삽입 정렬 > 퀵 정렬 > 선택 정렬
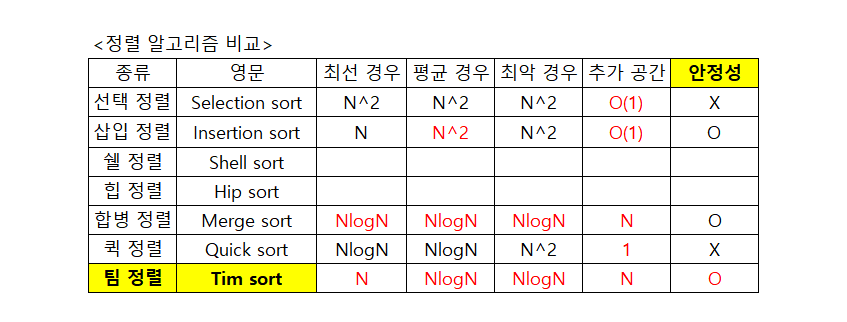
정렬 알고리즘 비교