사진: Unsplash의Todd Quackenbush

자연어처리의 핵심은 컴퓨터가 사람의 말을 이해하도록 하는 것입니다. 컴퓨터는 숫자만 이해할 수 있는 상태입니다. 컴퓨터에 단어를 가르치기 위해서는 숫자만을 사용해서 단어의 의미를 설명해야 할 것입니다.

가장 단순하게는 각 단어에 사전 순서(ㄱㄴㄷ..)대로 숫자를 매기는 방법이 있을 것입니다. 하지만 이 방법은 전혀 숫자가 단어의 의미를 담지 못하고 있습니다. 컴퓨터가 단어의 의미를 이해하지 못하면 큰 문제가 발생합니다.

예를 들어 네이버 검색창에 '삿포로 숙소'를 검색했을 때 제대로 된 검색 시스템이라면 '삿포로 게스트 하우스', '삿포로 료칸', '삿포로 호텔'과 같은 유사 단어에 대한 결과도 함께 보여줄 수 있어야 합니다. 하지만 단어간 유사성을 계산할 수 없다면, '게스트 하우스'와 '료칸'과 '호텔'이라는 연관 검색어를 보여줄 수 없습니다.

그렇다면 사람들은 어떻게 단어의 의미를 정리하려는 노력을 해왔을까요? 바로 단어의 족보를 만드는 것이었는데요, 가족의 뿌리를 알 수 있는 족보와 마찬가지로 단어 "car"을 포함하는 더 큰 개념으로 "motor vehicle(동력차)"라는 단어가 존재하는 것을 아래 그림을 통해 확인할 수 있습니다. 한편 "car"에 포함되는 작은 개념으로는 "SUV(스포트 유틸리티 자동차)","compact(소형차)", "hatch-back(해치백)" 등 더 구체적인 차종이 있음을 알 수 있습니다.

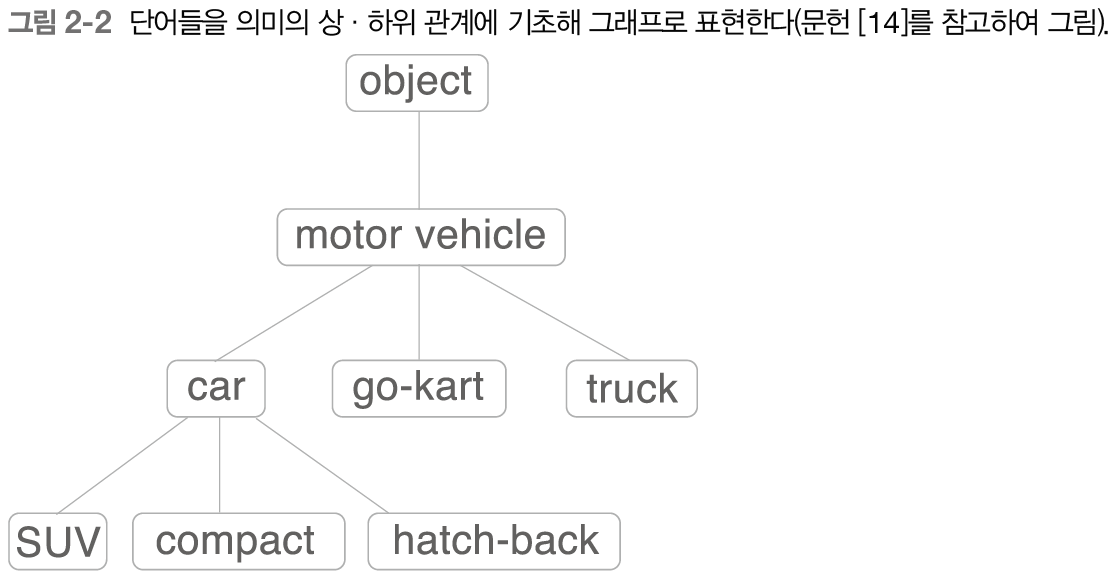
이를 통해 컴퓨터에게 모든 단어의 관계를 가르칠 수 있을 것입니다. (1세대 첫째는 "object", 3세대 셋째는 "truck"...) 드디어 네이버에 "car"를 검색하면 같은 세대에 있는 비슷한 단어인 "truck"의 결과도 나오게 됩니다.

하지만 위 방법도 완전한 것은 아니었습니다. 단어의 의미는 계속 바뀌기도 사라지기도 생겨나기도 하는 등 유동적이기 때문에 계속 족보를 수정해야 하는데 일일이 사람이 해주어야 하기 때문에 많은 시간과 돈이 필요합니다. 또 상황과 맥락에 따라 사용하는 단어의 차이와 어감 등의 정보는 족보에 담겨있지 않기 때문에 번역투의 이상한 말을 하기도 합니다.

이를 해결하기 위해 사람들은 긴 글에서 자동으로 단어의 의미를 뽑아내는 방법을 생각해냈습니다. 이 방법은 자동적일뿐 아니라 아주 효과적으로 단어 간 관계와 미묘한 의미의 차이, 심지어는 맥락까지도 파악할 수 있습니다.

동시 발생 행렬

"한 사람을 이해하고 싶으면 그 친구를 봐라"
-kyunghoon han

존경하는 한경훈 교수님의 말씀입니다. original은 존 퍼스의 "You shall know a word by the company it keeps."이라는 분포가설인데 위의 문구가 좀 더 와닿아서 인용해봤습니다.

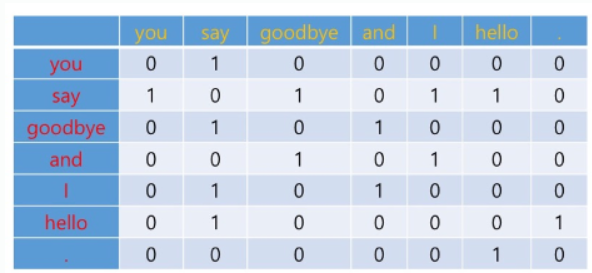
단어의 의미는 그 자체보다 그 단어가 사용된 맥락이 의미를 형성한다는 뜻입니다. 이를 반영한 방법이 co-occurunce 즉, 동시발생행렬입니다. 말이 너무 어렵기 때문에 아래 표를 통해 설명해보겠습니다.

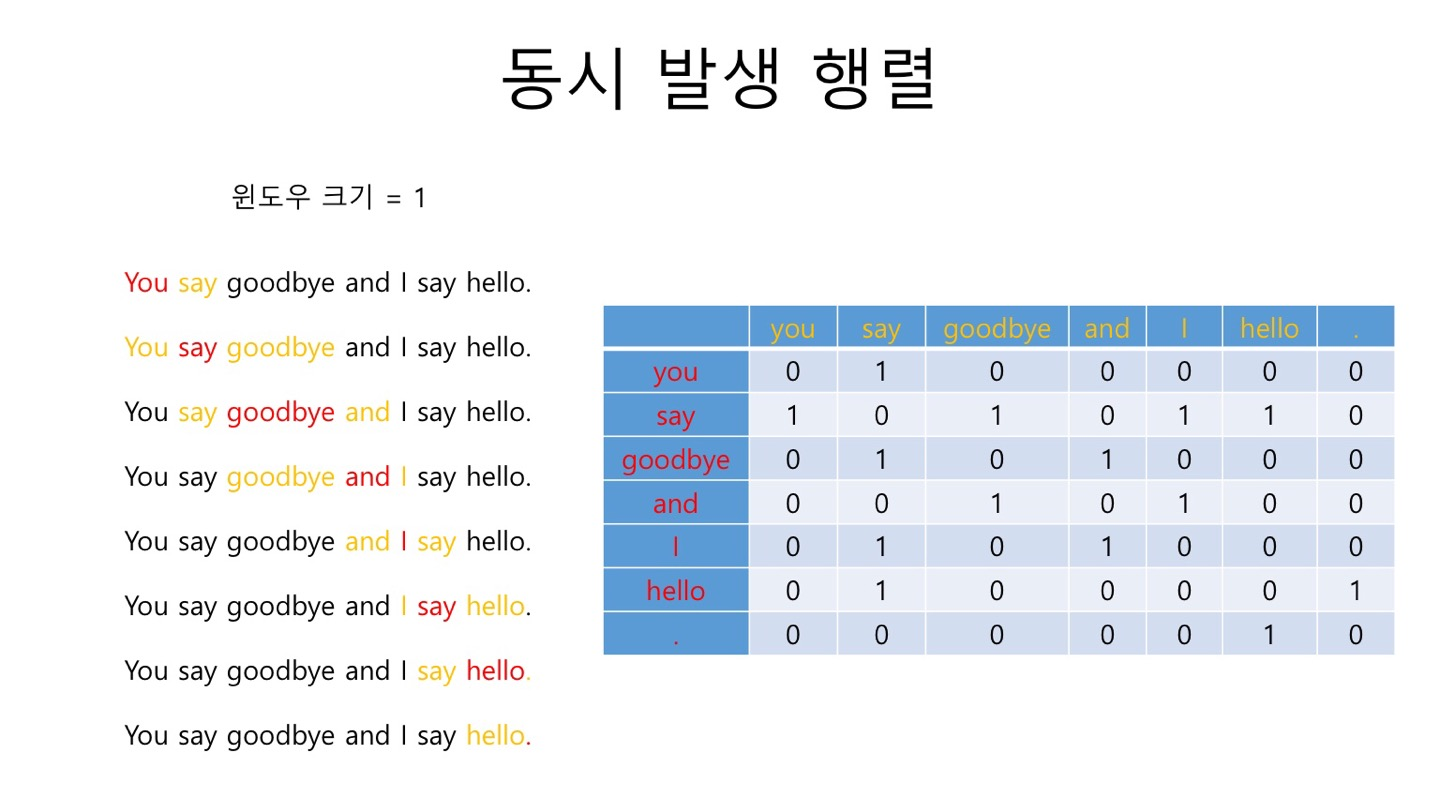
우리가 컴퓨터를 학습시키는 데에 사용할 문장은 아래와 같습니다.

"You say goodbye and I say hello."

동시발생행렬 방법을 통해 위 문장의 단어들 간 유사도를 구해보겠습니다.

먼저 window값, 즉 주변의 단어를 얼마나 유사도 측정에 사용할 지를 정해야 합니다. 문장이 짧기 때문에 주변 단어 1개씩을 사용하겠습니다. (window = 1)

이 때 맨 끝과 끝은 포함하지 않습니다.

따라서 "You"의 주변 글자는 "say",
"say"의 주변 글자는 "You", "goodbye", "I", "hello"
"goodbye"의 주변 글자는 "say", "and"
"and"의 주변 글자는 "goodbye", "I"
"I"의 주변 글자는 "and", "say"
"say"의 주변 글자는 "I", "hello"
"hello"의 주변 글자는 "say", "."
"."의 주변 글자는 "hello"입니다.

이를 표로 그리면 다음과 같이 나타낼 수 있습니다.

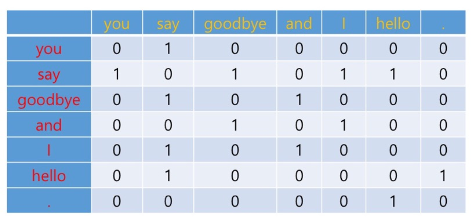
corpus(학습용 문장)를 입력하면 동시발생행렬을 반환하는 코드입니다.

import numpy as np

text = 'You say goodbye and I say hello.'

def preprocess(text):
    text = text.lower()
    text = text.replace('.', ' .')
    words = text.split(' ')

    word_to_id = {}
    id_to_word = {}
    for word in words:
        if word not in word_to_id:
            new_id = len(word_to_id)
            word_to_id[word] = new_id
            id_to_word[new_id] = word

    corpus = np.array([word_to_id[w] for w in words])
    vocab_size = len(id_to_word)

    return corpus, word_to_id, id_to_word, vocab_size
    
def create_co_matrix(corpus, vocab_size, window_size=1):
    '''동시발생 행렬 생성

    :param corpus: 말뭉치(단어 ID 목록)
    :param vocab_size: 어휘 수
    :param window_size: 윈도우 크기(윈도우 크기가 1이면 타깃 단어 좌우 한 단어씩이 맥락에 포함)
    :return: 동시발생 행렬
    '''
    corpus_size = len(corpus)
    co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)

    for idx, word_id in enumerate(corpus):
        for i in range(1, window_size + 1):
            left_idx = idx - i
            right_idx = idx + i

            if left_idx >= 0:
                left_word_id = corpus[left_idx]
                co_matrix[word_id, left_word_id] += 1

            if right_idx < corpus_size:
                right_word_id = corpus[right_idx]
                co_matrix[word_id, right_word_id] += 1

    return co_matrix

코사인 유사도

동시발생행렬을 구했으면 이제 각 단어의 벡터를 기준으로 코사인 유사도를 구할 수 있습니다.

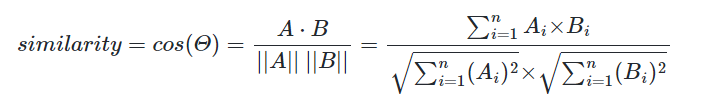
예를 들어 "you"와 "say"의 코사인 유사도를 구해보겠습니다.

"you"의 벡터는 [0,1,0,0,0,0,0]이고
"say"의 벡터는 [1,0,1,0,1,1,0]입니다.

두 벡터를 내적하면 0입니다.
분모를 구할 필요도 없이 코사인 유사도는 0입니다.

단어를 바꿔보겠습니다. "you"와 "i"의 코사인 유사도를 구해보겠습니다.

"you"의 벡터는 [0,1,0,0,0,0,0]이고
"i"의 벡터는 ____[0,1,0,1,0,0,0]입니다.

두 벡터를 내적하면 1입니다.
"you"의 벡터의 크기는 1입니다.
"i"의 벡터의 크기는 √2입니다.

계산해보면 두 벡터의 코사인 유사도는 1/√2입니다.

Cauchy-Schwarz 부등식에 의해서 코사인 유사도 값은 항상 -1과 1 사이에 있습니다. 코사인 유사도는 두 벡터가 가리키는 방향이 얼마나 비슷한 가를 나타내는 야입니다. 같은 방향이면 1이고, 반대 방향이면 -1입니다.

따라서 "you"는 코사인 유사도가 0인 "say"보다 코사인 유사도가 1/√2인 "i"에 더 유사하다고 할 수 있습니다.

코사인 유사도를 코드로 구현하는 방법은 다음과 같습니다.

def cos_similarity(x, y, eps=1e-8):
    '''코사인 유사도 산출

    :param x: 벡터
    :param y: 벡터
    :param eps: '0으로 나누기'를 방지하기 위한 작은 값
    :return:
    '''
    nx = x / (np.sqrt(np.sum(x ** 2)) + eps)
    '''
    normalize 과정
    원소들을 다 제곱해서 다 더한 뒤 루트 씌워주면 벡터의 크기이다.
    각 원소에 벡터의 크기를 나누면 벡터의 크기가 강제로 1이 된다

    eps: 아주 작은 수의 대명사

    '''
    ny = y / (np.sqrt(np.sum(y ** 2)) + eps)
    return np.dot(nx, ny)
    '''
    nx와 ny를 내적
    nx: normalized x = x / |x|
    ny: normalized y = y / |y|
    cos similarity = nx ⋅ ny = x * y/(|x| * |y|)
    '''

PPMI

동시발생행렬의 한계는 고빈도 단어가 포함된 두 단어의 유사도가 고평가된다는 점입니다. 상식적으로 "the", "car", "drive"를 비교하면 "the"와 "car"보다 "car"와 "drive"이 더 관련도가 높아보입니다. 하지만 막상 동시 발생 횟수를 구해보면 "the"와 "car"이 훨씬 많습니다. 이는 단순히 "the"가 어디서나 자주 등장하는 단어이기 때문에 나타나는 현상입니다. 이를 보정하기 위해서 "the"와 "car"의 동시 발생 확률을 분자로 하고"the"의 빈도 확률과 "car"의 빈도 확률의 곱을 분모로하여 밑이 2인 log를 취해주는 PMI 방법을 사용합니다. (log의 밑이 2인 이유는 컴퓨터의 정보 처리 방식이 이진수인 것과 관련이 있습니다.) 이렇게 보정을 하면 p(the, car)가 p(car,drive)보다 크지만 이를 상쇄하고도 남을 만큼 p(the)가 p(drive)보다 크기 때문에 아래와 같은 부등식이 성립하는 것을 납득할 수 있습니다.

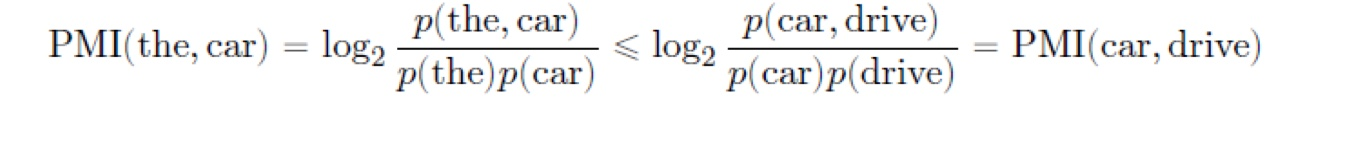
하지만 PMI도 두 단어의 동시 발생 횟수가 0이면 log_2(0) = -∞
이라는 오류가 발생할 수 있기 때문에 음수는 모두 0으로 변환하고 양수만 유지하는 PPMI를 사용하겠습니다.

def ppmi(C, verbose=False, eps = 1e-8):
    '''PPMI(점별 상호정보량) 생성

    :param C: 동시발생 행렬
    :param verbose: 진행 상황을 출력할지 여부
    :return:
    '''
    M = np.zeros_like(C, dtype=np.float32)
    N = np.sum(C)
    S = np.sum(C, axis=0)
    total = C.shape[0] * C.shape[1]
    cnt = 0

    for i in range(C.shape[0]):
        for j in range(C.shape[1]):
            pmi = np.log2(C[i, j] * N / (S[j]*S[i]) + eps)
            M[i, j] = max(0, pmi)

            if verbose:
                cnt += 1
                if cnt % (total//100 + 1) == 0:
                    print('%.1f%% 완료' % (100*cnt/total))
    return M

차원 축소

PPMI행렬을 구하면 이제 드디어 차원 축소를 수행할 수 있습니다. 동시발생행렬을 그대로 차원 축소할 경우 손실되는 정보가 너무 많습니다. 하지만 PPMI행렬을 SVD분해하여 U를 2차원까지 축소합니다. 더 자세한 내용은 다음 화에 계속...

결과 확인

이제 단어 간의 유사도를 2차원 평면 그래프 상에 나타내보겠습니다.

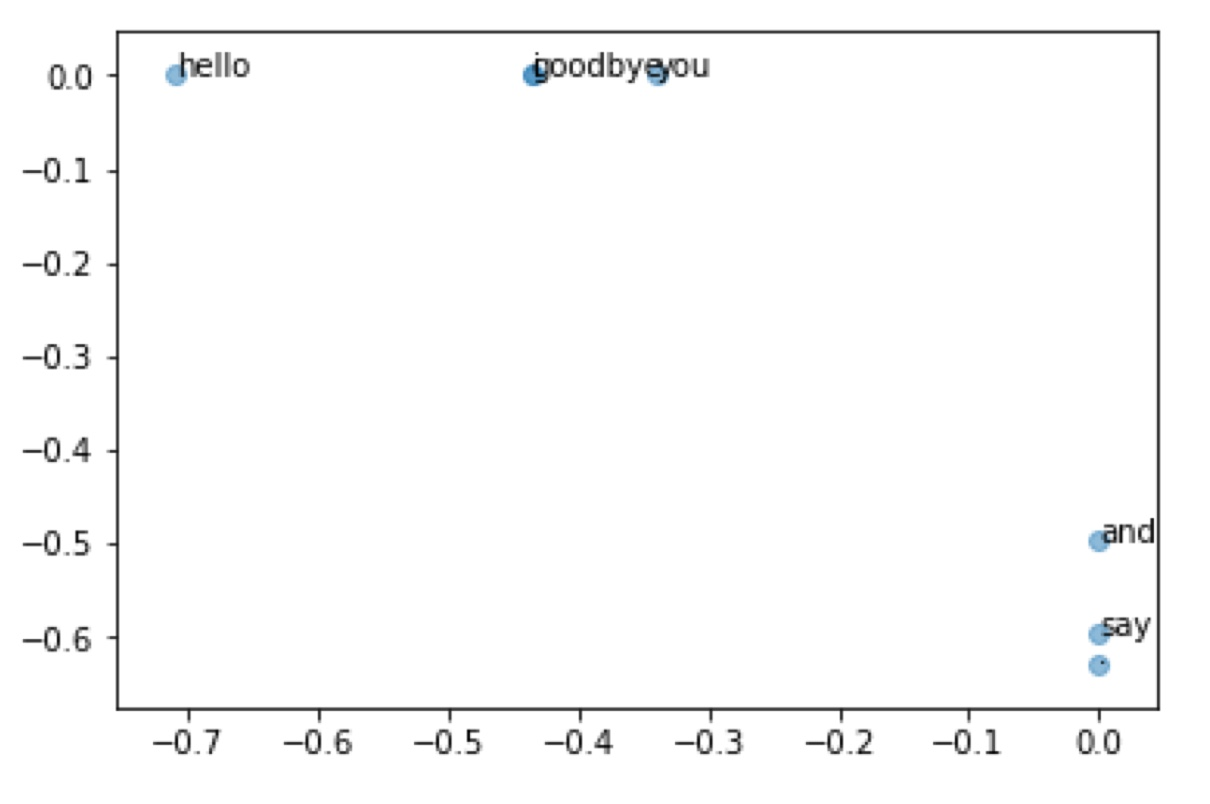
상식적으로 봤을 때 corpus 내에서 "you"와 가장 유사한 단어는 "i"인데 그래프를 확인해보면 꽤 가까이 위치한 것을 확인함으로써 유사도가 잘 구해졌다는 것을 알 수 있습니다.

이제 PTB 데이터셋을 활용하여 더 많은 단어를 학습시켜보겠습니다.

동시발생행렬을 구할 때 윈도우 크기는 2로 설정해주고, PPMI행렬로 변환해 준 뒤 SVD로 100차원까지 차원 축소를 해보겠습니다.

학습이 끝난 후 유사도가 가장 높은 상위 5개 단어를 출력해보겠습니다.

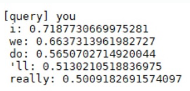
입력이 "you"일 때 유사도가 높은 순서로 "i", "we", "do", "'ll", "really"가 출력이 되었습니다.

다른 단어도 유사 단어들과 일반적인 상식으로 잘 맞아떨어지는 것을 확인할 수 있습니다.

출처

Unsplash의Fabrizio Conti 썸네일 사진
one-hot encoding의 문제점
family tree 이미지
단어 족보 이미지
동시발생행렬 이미지
핫도그 세 개 이미지
코드
코사인 유사도 이미지