이 글은 황용득 교수님의 수업 내용을 정리한 글입니다. 공부 목적으로 쓰는 글이며 velog에서 띄운 광고 수익은 저에게 일절 들어오지 않습니다.
목차
탐색 알고리즘
- 저장된 데이터에서 특정 조건을 만족하는 데이터를 찾는 알고리즘
키(key)
-
탐색 조건에 주목하는 항목(검색 조건에 따라 key가 결정)
-
예시)
탐색 조건: 털 색이 흰 색인 고양이를 찾습니다.
key: 털 색탐색 조건: 나이가 1개월 이상 3개월 미만인 새끼 고양이를 찾습니다.
key: 나이 -
키를 어떻게 배치하고 구조화하는 지에 따라 선형 탐색, 이진 탐색, 해시 탐색으로 나뉨
선형 탐색
선형 탐색(linear search)
- 선형(직선)으로 늘어선 데이터에서 원하는 키값을 가진 원소를 찾을 때까지 맨 앞에서부터 순서대로 검색하는 알고리즘(e.g.
for문)
선형 탐색의 종료 조건
-
검색할 값을 찾지 못하고 배열의 맨 끝을 지나간 경우 (검색 실패)
-
e.g. 배열 [3,5,1,8,2]에서 8 찾기
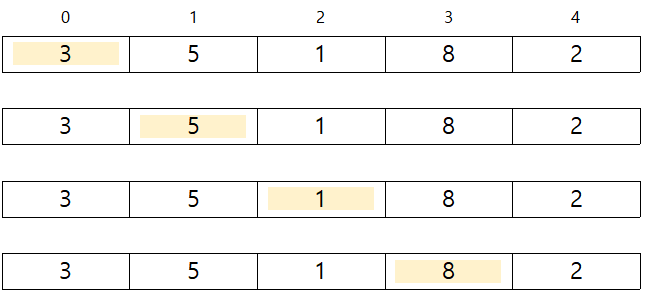
-
검색할 값과 같은 원소를 찾은 경우 (검색 성공)
-e.g. 배열 [3,5,1,8,2]에서 9 찾기
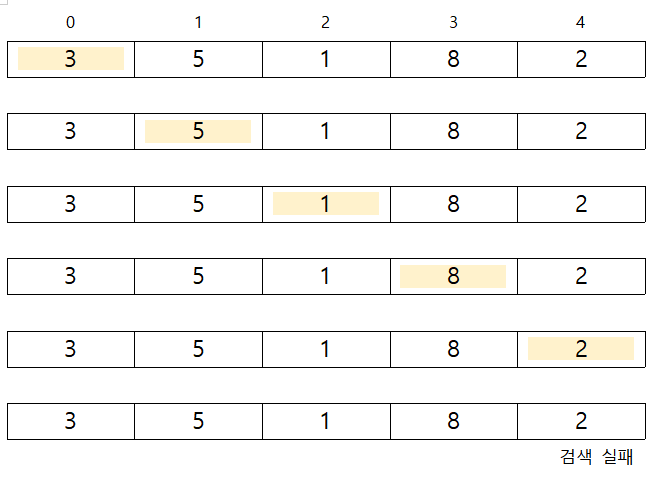
선형 검색
- 검색에 성공하면 인덱스를 반환
- 검색에 실패하면 -1을 반환
from typing import Any, Sequence
def linear_search(seq: Sequence, target: Any) -> int:
for i in range(len(seq)):
if seq[i] == target: # key와 target이 같다면
return i # 인덱스 반환(검색 성공)
return -1 # 검색 실패
print(linear_search([6,4,3,2,1,2,8],2))
print(linear_search([6,4,3,2,1,2,8],5))3
-1시간 복잡도
- O()
- 최선 경우: O()
- 최악 경우: O()
이진 탐색
이진 탐색(binary search)
- 반드시 정렬된 상태에서 시작해야 함
- 탐색 범위 정 중앙에 위치한 값과 찾고자 하는 타겟을 비교해 탐색 범위를 절반씩 줄여가며 찾는 방법
- 선형 탐색보다 빠름
이진 탐색의 수행시간
- O()
- 의 생략된 밑은 2이다.
이진 탐색으로 66을 찾는 과정
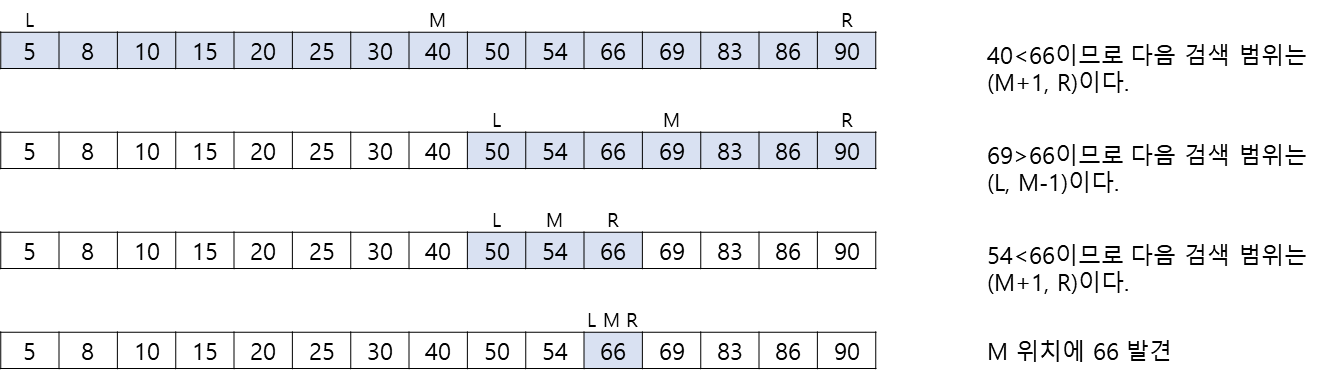
이진 탐색으로 12를 찾는 과정

반복적 이진 탐색
- O()
- 반복적: 재귀가 아닌
for문/while문을 사용
from typing import Any, Sequence
def binary_search_iter(seq: Sequence, target: Any) -> int:
left = 0 # 시퀀스의 첫 인덱스
right = len(seq) - 1 # 시퀀스의 마지막 인덱스
while left <= right: # 검색 대상이 하나라도 남아있으면 반복
mid = (left + right) // 2
if seq[mid] == target:
return mid # 검색 성공
elif seq[mid] > target: # target이 mid 왼쪽에 있으면
right = mid - 1 # 검색 범위를 왼쪽 절반으로 좁힘
else: # target이 mid 오른쪽에 있으면
left = mid + 1 # 검색 범위를 오른쪽 절반으로 좁힘
return -1
nums = sorted([6,4,3,2,1,7,8])
print(binary_search_iter(nums, 3))
print(binary_search_iter(nums, 5))2
-1재귀적 이진 탐색
- O()
def binary_search_recursive(seq: Sequence, target: Any) -> int:
def recur(left, right): # 앞서 정의한 함수 내에서만 호출 가능
if left > right:
return -1
mid = (left + right) // 2
if seq[mid] == target: # target 발견
return mid
elif seq[mid] > target: # target이 중앙 단어 기준 왼쪽에 있을 때
return recur(left, mid-1) # 검색 범위 축소하여 재탐색
else: # target이 중앙 단어 기준 오른쪽에 있을 때
return recur(mid+1, right) # 검색 범위 축소하여 재탐색
return recur(0, len(seq)-1) # 재귀호출 이용하여 반복 효과
nums = sorted([6,4,3,2,1,7,8])
print(binary_search_recursive(nums, 3))
print(binary_search_recursive(nums, 5))2
-1binary_search_recursive()함수는recur()함수를 이용하여 탐색 수행recur()함수는left와right사이에서target의 위치를 리턴하는 재귀함수
-left: 탐색 시작 인덱스
-right: 탐색 종료 인덱스
이진 탐색의 시간복잡도
-
O(): 한 번 탐색할 때마다 탐색범위가 절반으로 감소한다.

-
N = 8일 때, 중앙값와 타깃의 비교(= O())가 3(= )번 일어남
= 3
2 x 2 x 2 = 8
2를 세 번 곱하면 8이 되고
8을 2로 세 번 나누면 1이된다.
즉, 중앙값과 타깃 비교를 데이터가 하나만 남을 때까지(= 중앙값과 타깃이 일치할 때까지) 반복한다면 최악의 경우 번 반복하게 된다.
선형 탐색 VS 이진 탐색
- 1만 번 검색하는 데 걸리는 시간 복잡도 비교: 약 762 배 차이
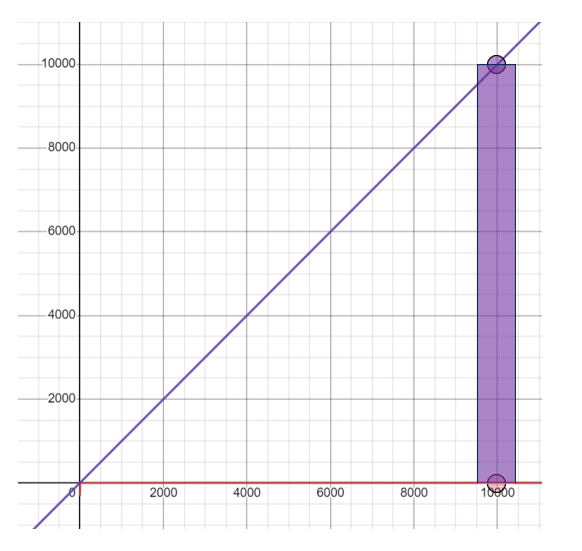
- 1만 번 검색하는 데 실제 걸리는 시간 비교: 약 100배 차이(GPU기준)
- T4 GPU
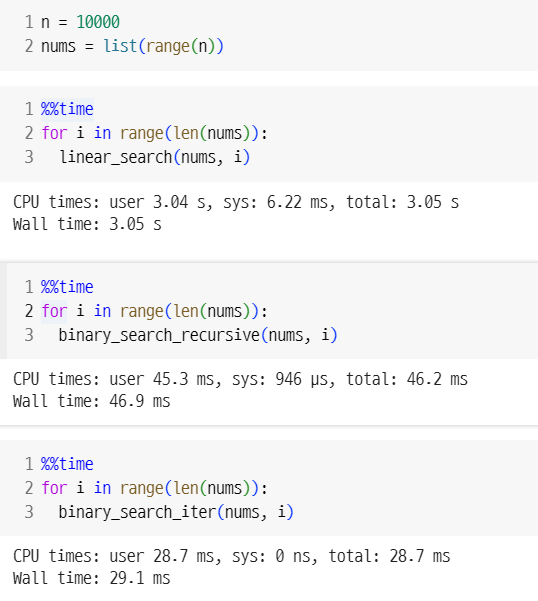
실무에서는 실제 측정 시간이 더 쓸모 있는 듯하다.
해시 탐색

위키백과 감자

CJ THE MARKET 해쉬브라운 냉동감자 1.2kg
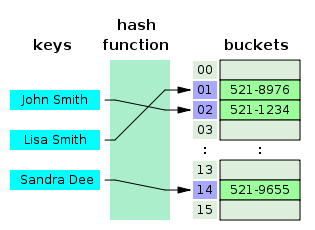
- 해싱(Hashing): 키를 해시 함수를 이용해 배열의 인덱스로 변환시켜 데이터를 배열에 저장하는 방식
- 해시 함수
- 키를 인덱스(N >=0)로 변환시키는 함수 - 해시 탐색
- 해싱을 이용하여 매우 빠르게 데이터를 검색하는 방법 - 해시 탐색의 시간 복잡도
- 대부분의 경우 O()
- 드물게 O() - 파이썬의 딕셔너리를 통해 해시 탐색을 할 수 있다.
- 해시값(해시주소)
- 해시 함수가 계산한 값 - 해시 테이블
- 데이터를 해시값에 따라 저장한 배열
해시 충돌
- 서로 다른 입력값에 대해 해시 함수가 반환한 인덱스가 중복될 경우

출처: 해시 충돌
- 해결법
1) 체이닝(Chaining): 연결 리스트를 통해 동일 인덱스에 여러 데이터 저장
2) 개방 주소법: 중복되면 다른 위치에 저장

출처: IT 기술면접 준비자료