이 글은 황용득 교수님의 수업 내용을 정리한 글입니다. 공부 목적으로 쓰는 글이며 velog에서 띄운 광고 수익은 저에게 일절 들어오지 않습니다.
목차
- 트리 정의
- 트리 용어
- 이진트리, 포화이진트리, 완전이진트리
- 이진트리를 배열로 표현
- 트리 탐색
1. 트리 정의
트리의 정의
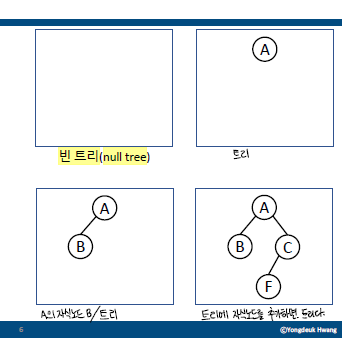
- 재귀적 정의(자기 자신을 활용한 정의)
- 비어있는 것은 트리이다. (null tree)
- 노드 하나만 있는 것은 트리이다.
- 트리에 자식노드를 추가한 것은 트리이다.
- 비재귀적 정의
- 사이클(루프)이 없는 연결된 그래프

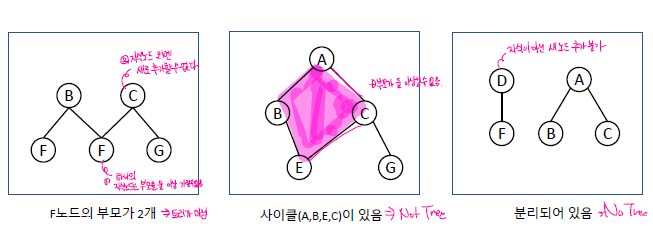
- 트리가 아닌 예시
트리의 활용
- 노드(node) (= 정점 = vertex)
- 엣지(edge) (= 간선 = 가지 = link)
트리의 구성
- 계층적 데이터를 효과적으로 다룰 수 있음.
- 계층적 데이터
- 조직도- 파일 시스템
- 데이터베이스
- 웹사이트
2. 트리 용어
루트
- 트리의 최상위 노드
- 특징
- 어떤 트리도 루트는 1개 이하
-루트 노드는 전체 노드를 대표- Alphabet에서 가장 유명한 회사는 Google이므로 Alphabet의 대명사가 Google인 것처럼 트리 T에서 가장 최상위 노드인 A는 트리 T의 대명사가 될 수 있음(트리 A)
부모 노드
-
하위 노드들과 연결되어 있는 노드
-
예시
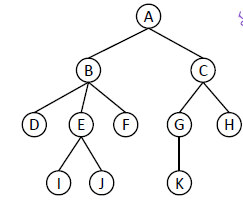
A는B,C의 부모B는D,E,F의 부모C는G,H의 부모E는I,J의 부모G는K의 부모
자식 노드
- 상위 노드들과 연결되어 있는 노드
- 특징
- 루트 노드는 자식노드가 아니다.
- 루트 노드를 제외한 모든 노드는 자식 노드이다. - 예시
B,C는A의 자식D,E,F는B의 자식I,J는E의 자식G,H는C의 자식K는G의 자식
형제(siblings)
- 같은 부모를 갖는 노드들
- 예시
B,C는 형제D,E,F는 형제G,H는 형제I,J는 형제
조상(ancestor) 노드
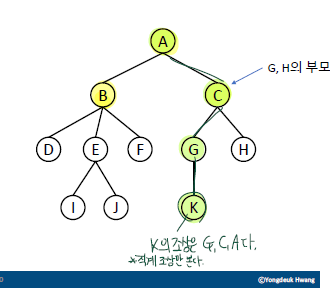
- 어떤 노드에서 위쪽으로 엣지를 따라 올라가면서 만나는 노드
- 예시
A,B는E의 조상E,B,A는J,I의 조상
...
자손(descendant) 노드
- 어떤 노드에서 아래쪽으로 엣지를 따라 내려가면서 만나는 모든 노드
- 특징
- 자식들의 자식은 모두 자손이다. - 예시
G,H,K는C의 자손D,E,F,I,J는B의 자손
...
리프(leaf) 노드
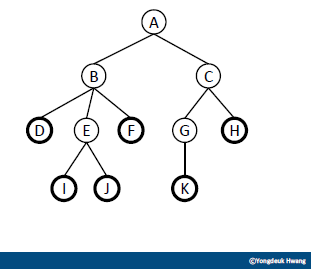
- 자식이 없는 노드
- 리프 노드(leaf node) = 외부 노드(external node) = 단말노드(terminal node)
- 예시
-D,F,H,I,J,K는 리프 노드이다.
내부 노드(internal node)
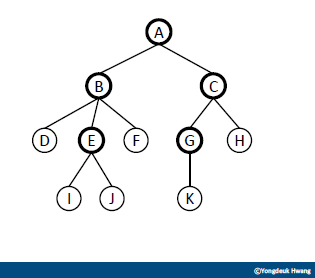
- 자식이 있는 노드
- 내부 노드(internal node) = 비단말 노드(non-terminal node)
- 예시
-A,B,E,G는 내부 노드이다.
레벨(level)
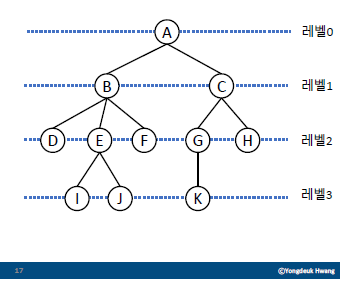
- 루트에서 얼마나 멀리 떨어져 있는 지
- 레벨(level) = 깊이(depth)
- 루트의 레벨은 0
- 루트에서 엣지가 하나씩 아래로 뻗어나갈 때마다 레벨이 1씩 증가
차수(degree)
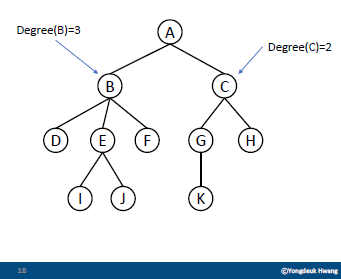
- 노드가 갖는 자식 수
노드의 높이(height)
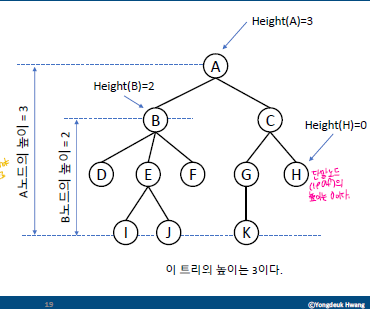
- 특정 노드에서 가장 멀리있는 리프까지의 거리
- 트리의 높이
- 루프 노드의 높이- 레벨의 최대값
- 특징
- 비어있는 트리의 높이는 -1
서브 트리(subtree)
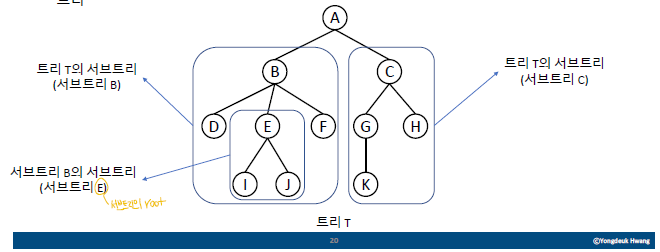
- 트리 안의 작은 트리
3. 이진트리, 포화이진트리, 완전이진트리
이진트리
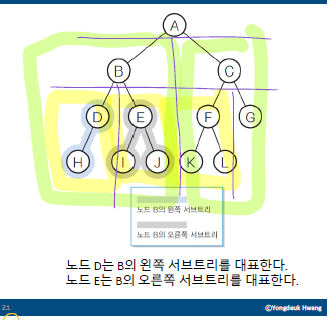
- 모든 노드가 2개 이하의 자식을 가지는 트리
- 특징
- 왼쪽 자식과 오른쪽 자식으로 구분 - 왼쪽 서브트리
- 왼쪽 자식을 루트로하는 서브 트리 - 오른쪽 소브트리
- 오른쪽 자식을 루트로하는 서브 트리
포화이진트리 vs 완전이진트리
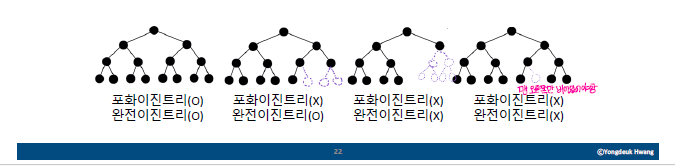
- 포화이진트리( perfect binary tree)
- 모든 레벨이 노드들로 꽉 찬 이진트리 - 완전이진트리(complete binary tree)
- 마지막 레벨을 제외한 각 레벨이 노드들로 꽉 참
- 마지막 레벨에서는 왼쪽부터 노드가 빠짐없이 채워짐- 포화이진트리는 완전이진트리이다. (역은 성립x)
이진트리 속성
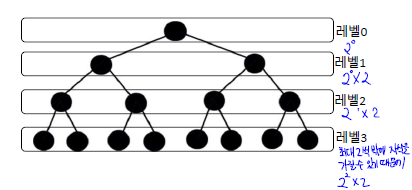
- 이진트리 레벨
k의 최대 노드 수 = - 높이가
h인 이진트리가 가질 수 있는 최대 노드 수 =
- 레벨 0(루트 노드)은 하나의 노드밖에 가질 수 없기 때문
n개의 노드를 갖는 완전이진트리의 높이
- 높이가
h인 완전이진트리가 가질 수 있는 최대 노드 수 =
- 완전이진트리는 이진트리이기 때문 - 높이가
h인 완전이진트리가 가질 수 있는 최소 노드 수 =
- 높이가h-1인 완전이진트리의 최대 노드 수에 1을 더한 것
- 높이가
h인 완전이진트리가 가질 수 있는 노드 수 범위: n개의 노드를 가진 완전이진트리의 높이 = floor()
=
=h는 트리의 높이이므로 정수
=>h= floor()floor()는 소수점 이하 버리는 파이썬 함수
4. 이진트리를 배열로 표현
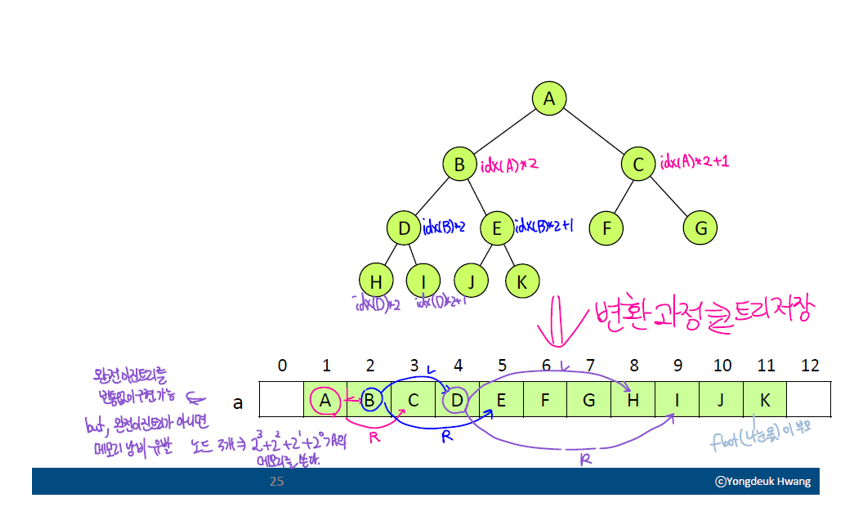
- 배열(파이썬 리스트)을 이용하여 완전이진트리 구현
- 인덱스 0 자리는 비워둠(
None) - 루트노드의 인덱스 번호는 1
a[i]의 부모는a[i/2]a[i]의 왼쪽 자식은a[2*i]a[i]의 오른쪽 자식은a[2*i + 1]
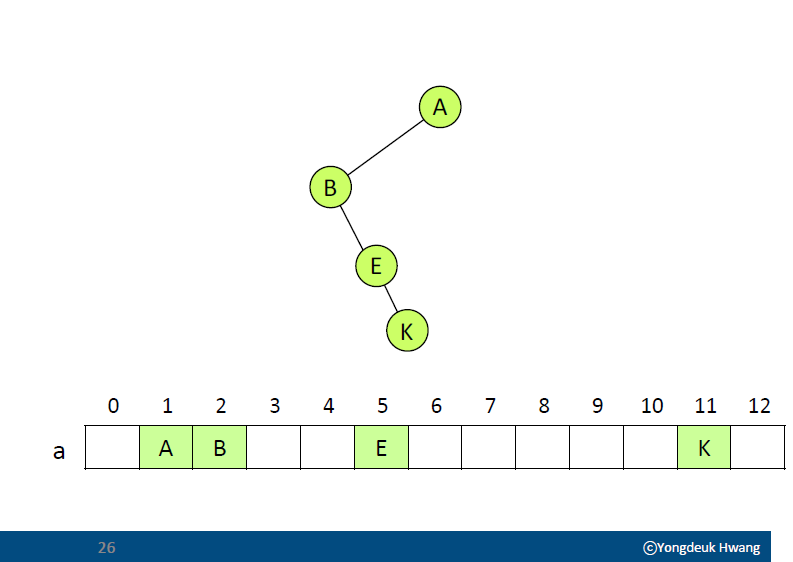
- 인덱스 0 자리는 비워둠(
- 완전이진트리가 아닌 이진트리
- 메모리 낭비 발생할 수 있음
5. 트리 탐색
너비 우선 탐색(breadth-first-search)
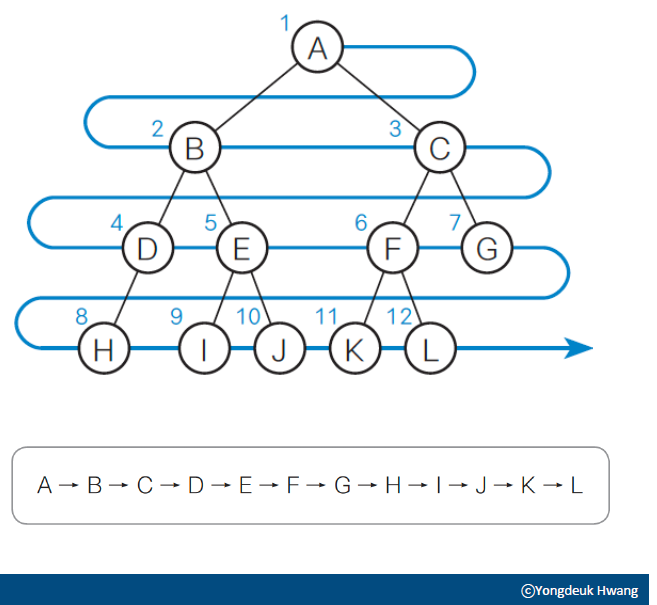
- 폭 우선 검색, 가로 검색, 수평 검색
- 낮은 레벨부터 왼쪽에서 오른쪽으로 검색
- 한 레벨에서 검색을 마치면 다음 레벨로 내려가는 방법
깊이우선탐색(depth-first-serach)
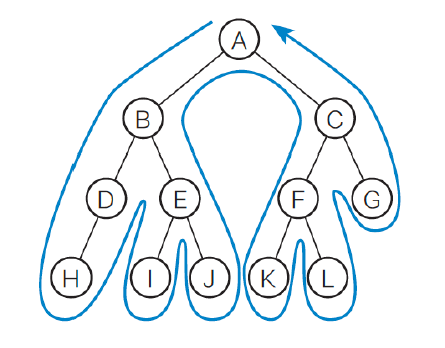
- 세로 검색, 수직 검색
- 리프에 도달할 때까지 아래쪽으로 내려가면서 검색하는 것을 우선으로 함
- 리프에 도달해서 더 이상 검색할 곳이 없으면 일단 부모 노드로 돌아가고 그 다음 자식 노드로 내려감
- 전위 순화(preorder): 노드 방문 -> 왼쪽 자식 -> 오른쪽 자식


