트리 Tree

노드로 구성된 계층적 자료구조.
노드(node)들과 노드들을 연결하는 간선(edge)들로 구성되어 있다.

트리는 1개 이상의 노드로 구성되며, 하나의 루트 노드를 갖는다.
최상위 노드인 루트는 0개 이상의 자식 노드를 갖는다.
그 자식 노드의 자식 노드가 존재하는 구조가 반복된다.
트리는 루트와 전체 트리의 부속트리로 구성된다고 말할 수 있다.

구조와 용어

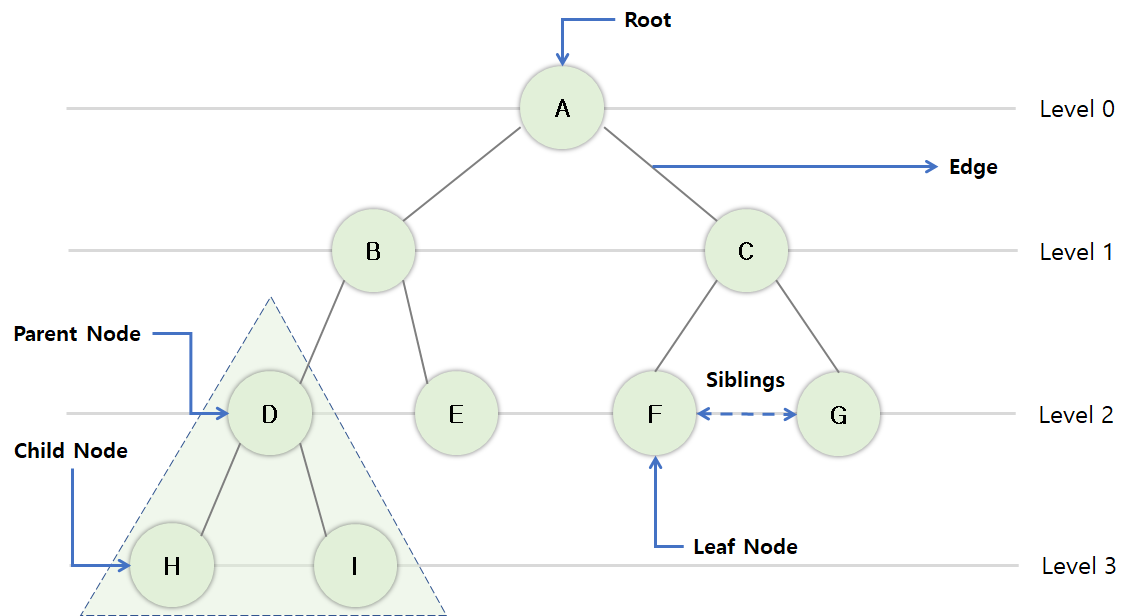
• 루트 노드(root node)
  • 부모가 없는 최상위 노드.
• 단말 노드(leaf node)
  • 자식이 없는 노드.
  • 트리의 맨 마지막에 존재하는 노드.
• 내부 노드(internal node)
  • 단말 노드가 아닌 노드.
• 간선(edge)
  • 노드를 연결하는 선.
  • link, branch
• 부모 노드(parent node)
  • 노드를 서브트리로 갖는 노드.
• 자식 노드(child node)
  • 부모에 속하는 노드.
• 형제(sibling node)
  • 같은 부모를 갖는 노드.
• 노드의 크기(size)
  • 자신을 포한한 모든 자손 노드의 갯수.
• 노드의 깊이(depth)
  • 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수.
• 노드의 레벨(level)
  • 트리의 특정 깊이를 가지는 노드의 집합.
  • 루트로부터의 노드의 깊이.
• 노드의 차수(degree)
  • 노드에 연결된 또 다른 노드의 갯수.
  • 각 노드가 지닌 가지의 수.
• 트리의 차수(degree of tree)
  • 트리의 최대 차수.
• 트리의 높이(height)
  • 루트 노드에서 가장 깊숙히 있는 노드의 깊이.
  • 트리에 속한 노드의 최대 레벨.

트리의 특징

• 그래프의 한 종류이다. 최소 연결 트리라고도 불린다.
  • 사이클이 없는 하나의 연결 그래프(Connected Graph)
  • 또는 DAG(Directed Acyclic Graph, 방향성이 있는 비순환 그래프)의 한 종류이다.
    • loop, circuit 없다.
    • cycle 없다.
• 비선형 자료구조. 계층적 관계를 표현한다.
• 노드가 N개인 트리는 항상 N-1개의 간선(edge)를 가진다.
  • 즉, 간선은 항상 (정점의 개수 - 1)만큼을 가진다.
• 루트에서 어떤 노드로 가는 경로는 유일하다.
  • 두 개의 정점 사이에 반드시 1개의 경로만을 가진다.
• 한 개의 루트 노드만이 존재하고 모든 자식 노드는 한 개의 부모 노드만을 가진다.
  • 부모-자식 관계이므로 흐름은 top-bottom / bottom-up으로 이루어진다.
• 각 노드는 어떤 자료형으로도 표현 가능하다.
• 각 노드는 부모 노드로의 연결이 있을 수도 있고 없을 수도 있다.

트리의 종류

이진 트리(Binary Tree)

하나의 부모가 가질 수 있는 자식의 수가 최대 2개인 트리를 말한다.
모든 트리가 이진트리는 아니다.

   3    4
  / \    \
 1   2    5

포화 이진 트리(Perfect Binary Tree)

• 모든 레벨의 노드가 가득 차있는 트리.
• 모든 부모 노드가 두 개의 자식을 가지고 있는 트리.
• 차수(degree)가 2이다.
• 모든 노드가 가득 차있기 때문에 단말 노드부터 루트 노드까지의 높이가 같다.
• 노드 개수 : 2^(height-1).
  하단의 트리는 height가 2이기 때문에 2^3-1 = 7개의 노드를 갖는다.

        a
      /   \
     b     c
    / \   / \ 
   d   e f   g

완전 이진 트리(Complete Binary Tree)

• 마지막 레벨 바로 전까지는 꽉 차있고 마지막 레벨에서 왼쪽부터 차례대로 채워져 있는 트리.
• 마지막 레벨을 제외하고 모든 레벨이 꽉 채워져 있다.
• 마지막 레벨은 채워져있지 않아도 되지만 노드가 왼쪽에서 오른쪽으로 채워져야 한다.
• 새로운 노드를 추가할 때 왼쪽부터 추가하거나, 기존의 노드를 제거할 때 오른쪽부터 제거한다.
• 노드 개수 : n < 2^height-1.
• 완전 이진 트리의 개념은 힙(heap)과 관련이 있다.
  배열을 사용해 효율적으로 표현 가능하다.

       a
     /   \
    b     c
   / \   /
  d  e  f

편향 이진 트리(Skewed Binary Tree)

• 왼쪽 또는 오른쪽으로 편향되게 채워져 있는 트리.
• 각각의 높이에서 1개의 노드만 있다.
• height <= 노드의 개수 n <= 2^height-1

       a        a
      /          \
     b            b 
    /              \
   d                d 

왼쪽 편향          오른쪽 편향

정 이진 트리(Full Binary Tree)

• 모든 노드가 0개 또는 2개의 자식 노드만을 갖는 트리.
• 2*height + 1 <= 노드의 개수 n <= 2^(height+1) - 1

         a
        / \
       b   c
      / \
     d   e

이진 탐색 트리(Binary Search Tree, BST)

새로운 노드를 추가할 경우 부모 노드보다 값이 작으면 부모의 왼쪽자식, 부모 노드보다 값이 크면 부모의 오른쪽 자식에 노드를 추가한다.
모든 왼쪽 자식들 <= N < 모든 오른쪽 자식들 (모든 노드 N에 대해서 반드시 true)

구현

구현의 핵심은, 부모 노드에 자식과의 관계(주소)를 어떻게 저장할 것인가 에 대한 답에서 나온다.

배열을 사용하면 된다.
배열에 자식 노드들의 주소를 담아준다.
자식 노드를 생성하고 배열에 담으면, 자바스크립트가 알아서 주소를 맵핑해 준다.
자식을 삭제하기 위해서는 배열에서 해당 요소만 제거해주면 된다.

class Tree {
  //tree의 constructor를 구현.
  //tree의 자식 노드들을 children으로 할당하여 노드의 자식 노드들을 담을 수 있게 한다.
  constructor(value) {
    this.value = value;
    this.children = [];
  }
  //tree의 자식 노드를 생성 한 후에, 노드의 children에 push해준다.
  insertNode(value) {
    const childNode = new Tree(value);
    this.children.push(childNode);
  }
  // tree에서 value값을 탐색.
  // 현재 노드의 value 값이 찾는 값과 일치한다면 return.
  contains(value) {
    if (this.value === value) {
      return true;
    }
    // 노드가 가진 자식 노드를 순회하는 반복문으로 노드의 children 배열을 탐색한다.
    for (let i = 0; i < this.children.length; i += 1) {
      const childNode = this.children[i];
      if (childNode.contains(value)) {
        return true;
      }
    }
    return false;
  }
}