DFS

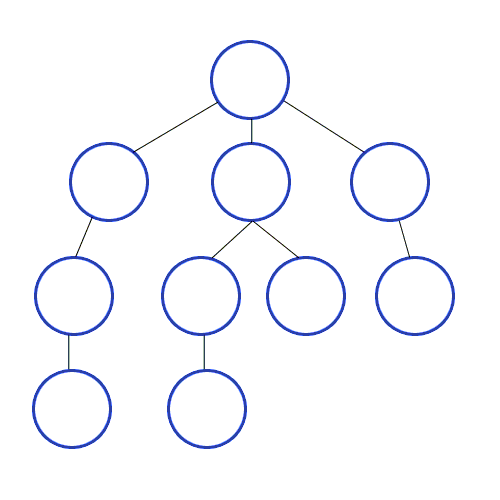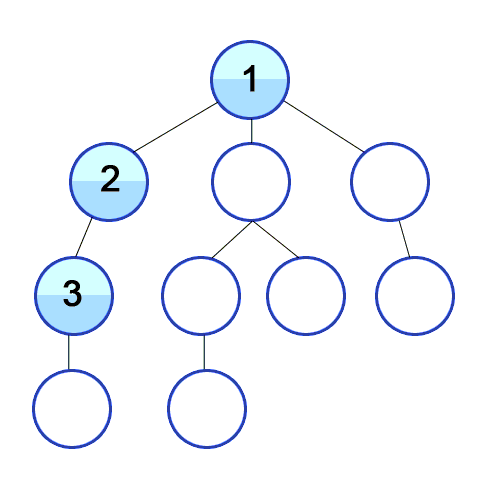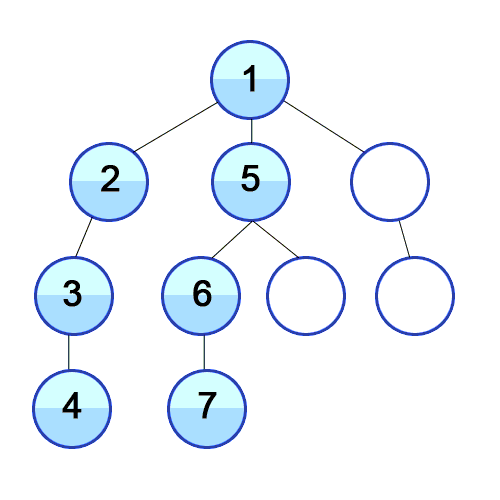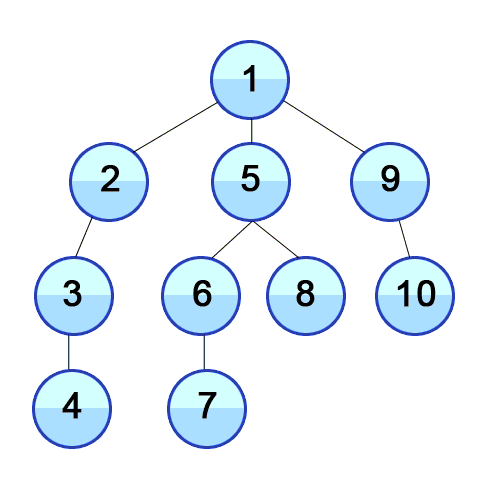
루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하고 넘어가는 방법.
넓게(wide) 탐색하기 전에 깊게(deep) 탐색한다.
모든 노드를 방문 하고자 하는 경우에 이 방법을 사용한다.

DFS가 BFS보다 좀 더 간단하다.
단순 검색 속도 자체는 BFS에 비해서 느리다.

스택이나 재귀 함수를 통해서 구현할 수 있는데 재귀 함수가 구현이 간편하므로 대부분 재귀 함수로 구현한다.

• 구현할 때 주의할 점 : 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사 해야 한다.
  • 이를 검사하지 않을 경우 무한루프에 빠질 위험이 있다.

DFS 알고리즘 구현방식

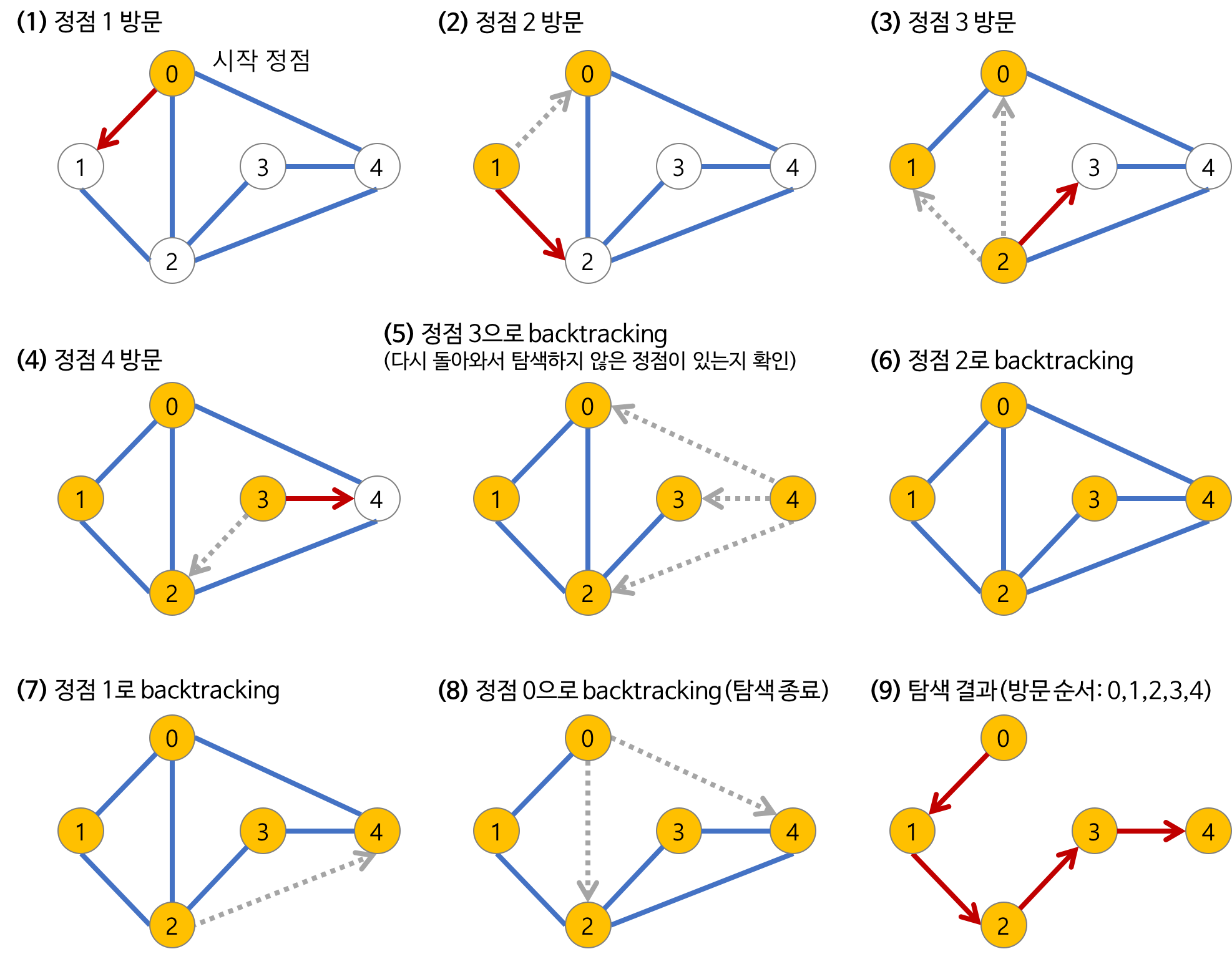
1. a 노드(시작 노드)를 방문
   • 방문한 노드는 방문했다고 체크한다!
2. a와 인접한 노드들을 차례로 순회
   • a와 인접한 노드가 없다면 종료
3. a와 이웃한 노드 b를 방문했다면, a와 인접한 또 다른 노드를 방문하기 전에 b의 이웃 노드들을 전부 방문해야 한다.
   • b를 시작 정점으로 DFS를 다시 시작하여 b의 이웃 노드들을 방문한다.
4. b의 분기를 전부 완벽하게 탐색했다면 다시 a에 인접한 정점들 중에서 아직 방문이 안 된 정점을 찾는다.
   • 즉, b의 분기를 전부 완벽하게 탐색한 뒤에야 a의 다른 이웃 노드를 방문할 수 있다는 뜻이다.
   • 아직 방문이 안 된 정점이 없으면 종료
   • 있으면 다시 그 정점을 시작 정점으로 DFS를 시작!

void search(Node root) {
  if (root == null) return;

  // 1. root 노드 방문
  visit(root);
  root.visited = true; // 1-1. 방문한 노드를 표시

  // 2. root 노드와 인접한 정점을 모두 방문
  for each (Node n in root.adjacent) {
    if (n.visited == false) { // 4. 방문하지 않은 정점을 찾는다.
      search(n); // 3. root 노드와 인접한 정점 정점을 시작 정점으로 DFS를 시작
    }
  }
}

DFS의 장점

• 현재 경로상의 노드들만 기억하면 되므로, 저장 공간의 수요가 비교적 적음
• 목표 노드가 깊은 단계에 있는 경우 해를 빨리 구할 수 있음
• 구현이 너비 우선 탐색(BFS) 보다 간단함

DFS의 단점

• 단순 검색 속도는 너비 우선 탐색(BFS) 보다 느림
• 해가 없는 경우에 빠질 가능성이 있음
  (사전에 임의의 깊이를 지정한 후 탐색하고, 목표 노드를 발견하지 못할 경우 다음 경로를 탐색하도록 함)
• 깊이 우선 탐색은 해를 구하면 탐색이 종료되므로, 구한 해가 최단 경로가 된다는 보장이 없음
  (목표에 이르는 경로가 다수인 경우 구한 해가 최적이 아닐 수 있음)

DFS의 시간 복잡도

• DFS는 그래프(정점의 수: N, 간선의 수: E)의 모든 간선을 조회한다.
  • 인접 리스트로 표현된 그래프: O(N+E)
  • 인접 행렬로 표현된 그래프: O(N^2)