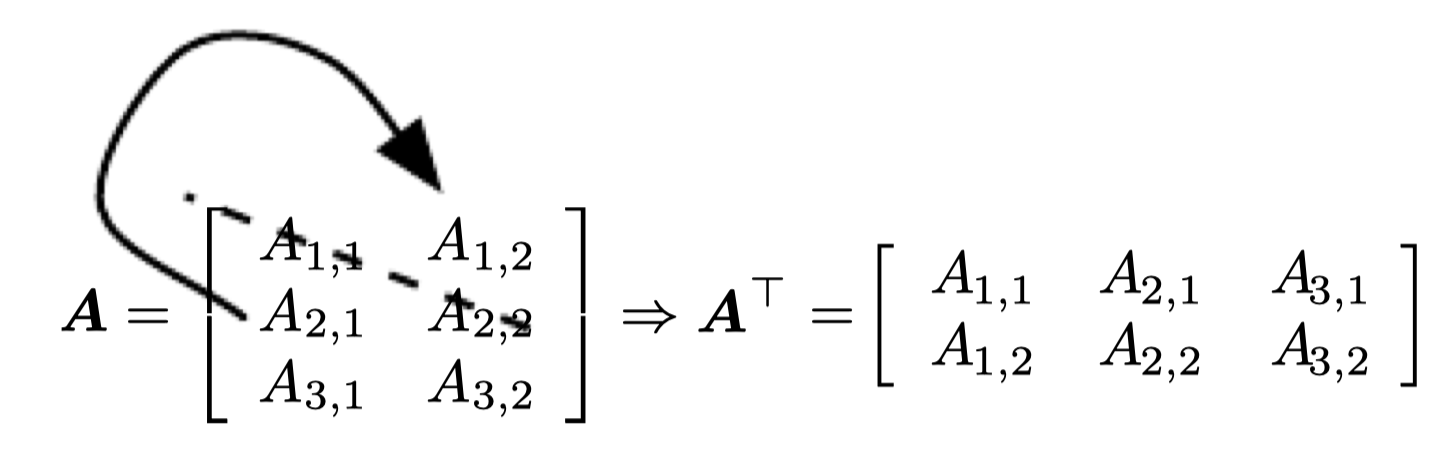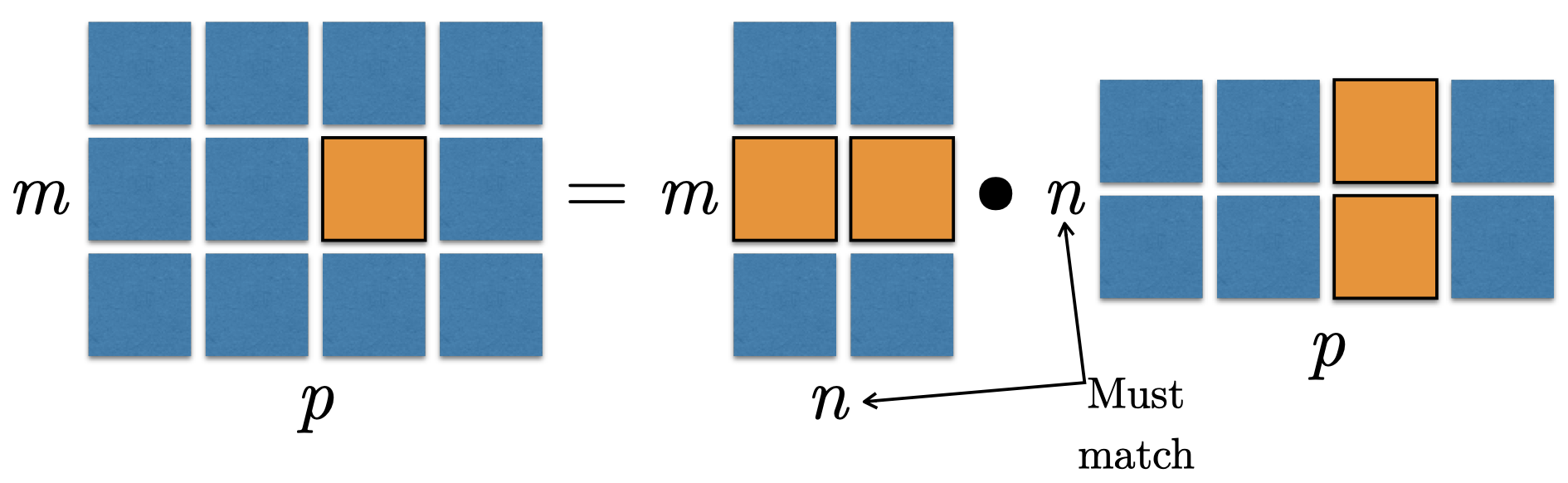TIMESTAMP
@200918 : PDF 정리 시작 (~가역행렬까지)
@200919 : PDF 정리 완료 (노름~)
@200919 : 본문 정리 시작 (~2.1)
들어가기전에
About this chapter
- 선형대수학은 과학과 공학 분야에 폭 넓게 사용되어 왔지만, 이산 수학(discrete)보다는 연속적인 형태(continuous)로 인해 상대적으로 컴퓨터 과학 분야에서는 잘 다뤄지지 않았다. 선형대수를 잘 이해하는 것은 많은 머신러닝 알고리즘이나 특히 딥러닝을 이해하고 수행하는데 필수적이다.
- 따라서 본 챕터를 통해서 필수적으로 알아야할 필수 선형대수 개념들을 다루고 본격적으로 딥러닝을 소개하고자 한다. 이번 챕터에서는 선형대수학 전체가 아닌 딥러닝에 관련된 부분만을 다룬다.
Scalars, Vectors, Matrices and Tensors
Scalars
- 스칼라는 정수, 실수, 유리수 등 하나의 숫자로 여기서는 이탤릭체로 표기한다
예시
- 실수 스칼라 s∈R
- 정수 스칼라 n∈N
Vectors
- 벡터는 1차원 배열(1D array)로 실수, 이진수, 정수 등이 될 수 있다. 종류와 크기에 따라서 다음과 같이 쓰며, 소문자 볼드체로 표기한다.
x=⎣⎢⎢⎢⎢⎡x1x2⋮xn⎦⎥⎥⎥⎥⎤∈Rn
- 순서에 따라 정렬되며, 인덱스(index)를 통해 각 숫자를 파악할 수 있다.
- 벡터는 공간에서의 점들로 생각할 수 있으며, 각 요소는 축에서의 좌표값을 제공한다.
예시 : 인덱스를 통해 벡터의 일부를 표현할 수 있다.
- if S={1,3,6}, then xS=⎣⎢⎡x1x3x6⎦⎥⎤
- 그 외에도, x−1,x−S 등으로 표기할 수 있다.
Matrices
- 행렬은 2차원 배열(2D array)로 종류와 크기에 따라서 다음과 같이 쓴다. 행렬은 대문자 볼드체로 표기하고, 행렬의 원소는 이탤릭체를 쓰지만 볼드를 쓰지 않는다.
A=[A1,1A2,1A1,2A2,2]∈Rm×n
예시 : f(A)i,j는 함수 f를 취한 행렬 A의 각 요소 (i,j)를 의미한다
Tensors
- 텐서는 다차원의 숫자의 배열로 0부터 고차원이 될 수 있다.
- 스칼라(0차원), 벡터(1차원), 행렬(2차원) 등
예시 : A와 같은 형태로 표현하며, 각 좌표 (i,j,k)에 대한 A의 요소는 Ai,j,k로 나타낼 수 있다.
Matrix Transpose
[예제1] 벡터와 스칼라
- x=[x1,x2,x3]T
벡터는 열이 하나인 행렬로, 벡터의 전치는 행이 하나인 행렬이 된다.
- a=a⊤
스칼라는 값 하나를 가지는 행렬로, 스칼라는 자기 자신을 전치행렬로 가진다.
[예제2] 행렬의 연산
- C=A+B where Ci,j=Ai,j+Bi,j
- D=a⋅B+c where Di,j=a⋅Bi,j+c
[예제3] 딥러닝에서의 브로드캐스팅
- C=A+b where Ci,j=Ai,j+bj
벡터 b가 행렬의 각 행에 더해질 수 있고, 이처럼 많은 곳에 해당 벡터를 복사하는 것을 broadcasting이라고 한다.
Multiplying Matrices and Vectors
Matrix (Dot) Product
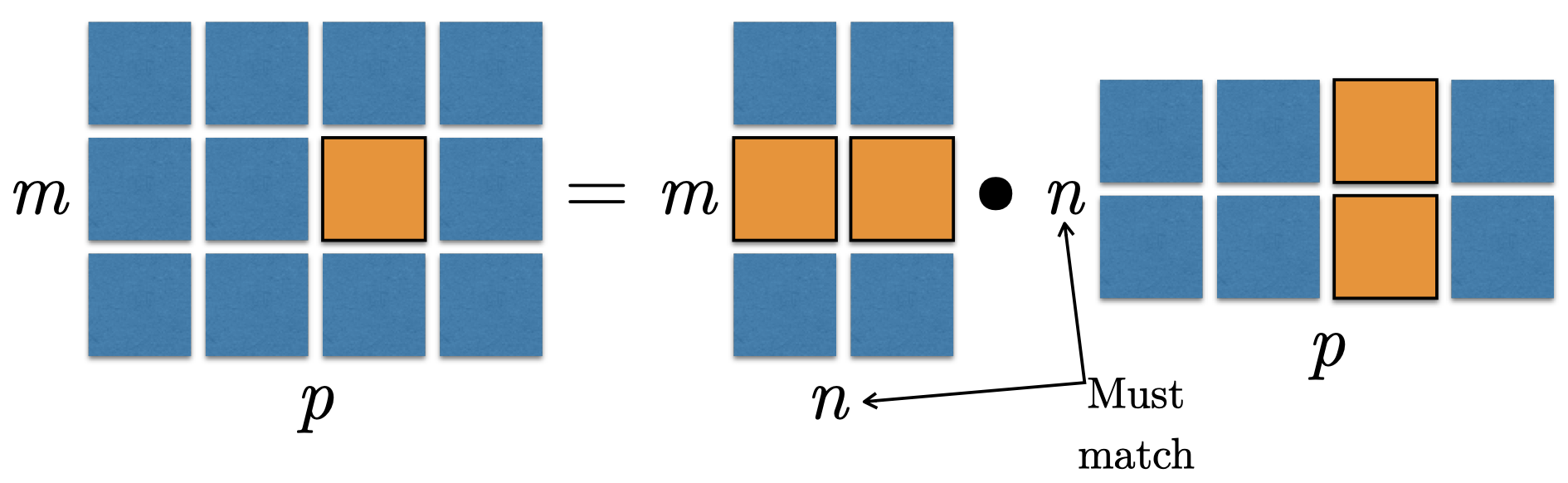
C=ABCi,j=k∑Ai,kBk,j
Identity Matrix
I3=⎣⎢⎡100010001⎦⎥⎤∀x∈Rn,Inx=x
Systems of Equations
Ax=bexpands toA1,:x=b1A2,:x=b2…Am,:x=bm
Solving Systems of Equations
- 선형 연립방정식은
(1) 해가 없거나
(2) 여러 해를 가지거나
(3) 단 하나의 해를 가진다
Matrix Inversion
A−1A=In
- 이를 이용하여 연립방정식을 풀 수 있다.
Ax=bA−1Ax=A−1bInx=A−1b
Invertibility
- 다음과 같은 경우에는 역행렬을 만들 수 없다.
- 행이 열보다 많을 때
- 열이 행보다 많을 때
- "linearly dependent", "low rank"
Norms
- 노름은 벡터의 크기를 나타내는 것으로, 0부터 해당 벡터의 지점까지의 거리와 유사하다.
f(x)=0⇒x=0f(x+y)≤f(x)+f(y)∀α∈R,f(αx)=∣α∣f(x)
-
Lp norm
∣∣x∣∣p=(i∑∣xi∣p)p1
- L2 norm (p=2)
- L1 norm (p=1) : ∣∣x∣∣1=∑i∣xi∣
- Max norm (infinite p) : ∣∣x∣∣∞=maxi∣xi∣
Special Matrices and Vectors
∣∣x∣∣2=1
A=A⊤
- Orthogonal matrix
A⊤A=AA⊤=IA−1=A⊤
Eigendecomposition
- 고유벡터와 고유값
(eigenvector, eigenvalue)Av=λv
- 대각화 가능 행렬의 고유값 분해
(eigendecomposition of a diagonalizable matrix)A=Vdiag(λ)V−1
- 모든 실수 대칭행렬은 직교하는 교유값 분해가 있다.
(orthogonal eigendecomposition)
A=QΛQ⊤
Effects of Eigenvalues
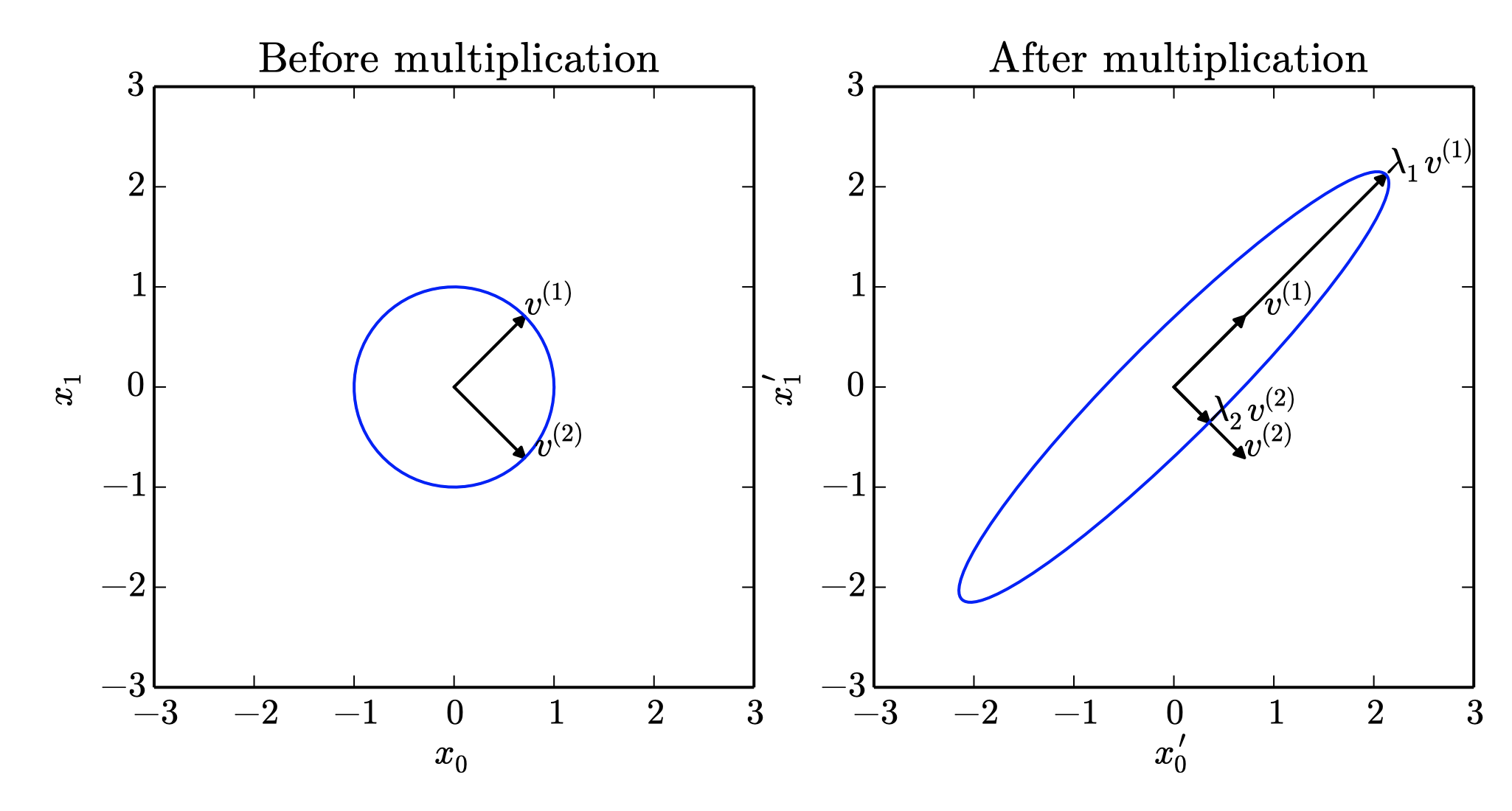
Singular Value Decomposition
- 특이값 분해는 고유값 분해와 유사하지만 좀 더 일반화된 형태로, 꼭 사각행렬일 필요가 없다.
A=UDV⊤
Moore-Penrose Pseudoinverse
- 오직 하나의 해를 가질 경우 : 역행렬과 동일하다
- 해가 없을 경우 : ∣∣Ax−y∣∣2 오차가 최소는 지점
- 많은 해를 가질 경우 : x의 노름이 최소가 되는 지점
Computing the Pseudoinverse
- SVD를 통해 의사역행렬의 계산이 가능하다
A+=VD+U⊤ Take reciprocal of non-zero entries
Trace
- 대각합
Tr(A)=i∑Ai,iTr(ABC)=Tr(CAB)=Tr(BCA)
Learning linear algebra
- Do a lot of practice problems
- Start out with lots of summation signs and indexing into individual entries
- Eventually you will be able to mostly use matrix and vector product notation quickly and easily