
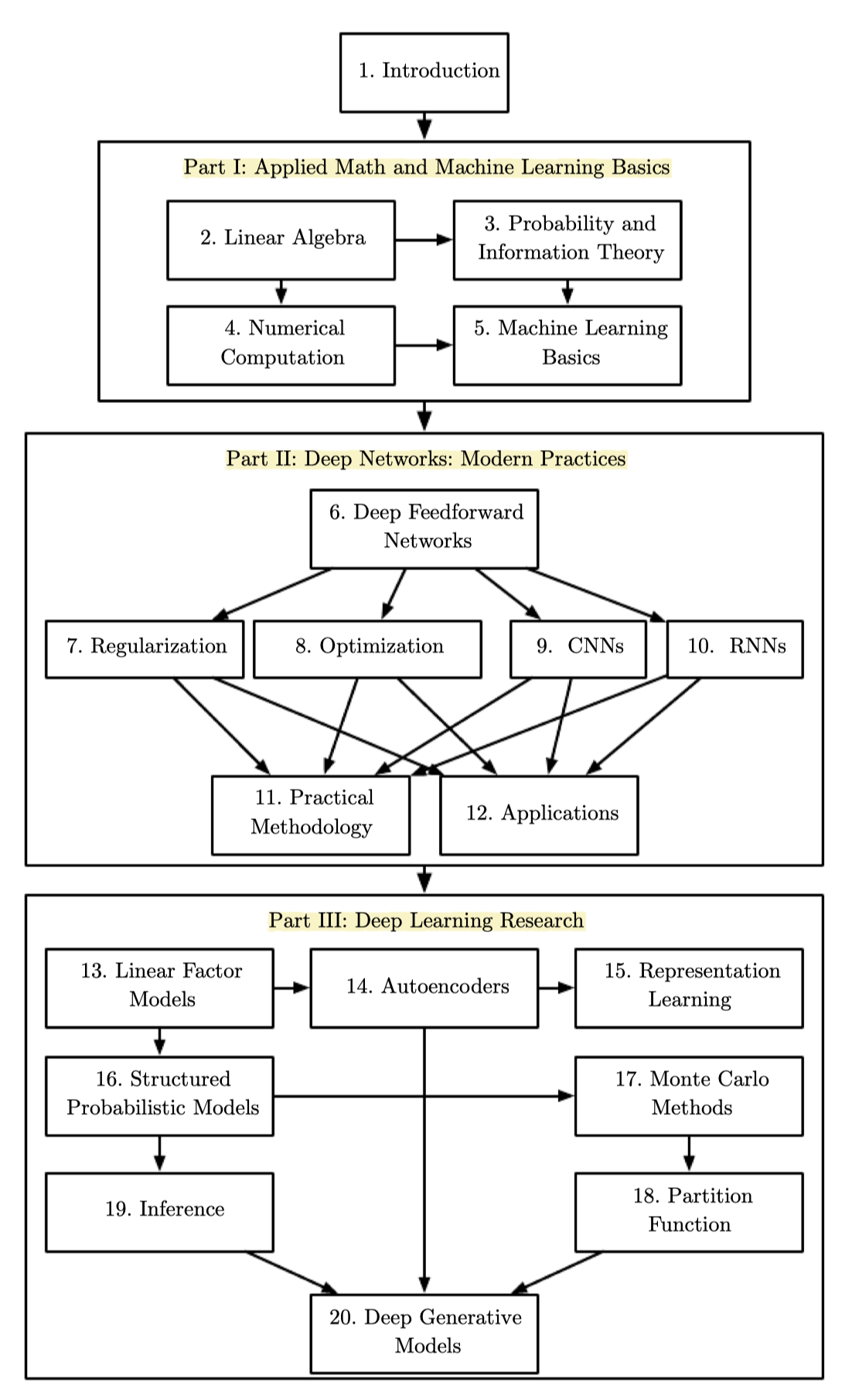
책은 크게 세 파트로 구성되어 있다.
- Part I : 선형대수학, 확률과 정보이론, 수치해석, 머신러닝
- Part II : 딥러닝 기초 개념
- Part III : 딥러닝 관련 연구들
Part I : 응용수학과 머신러닝 기초
-
딥러닝을 이해하는 데 필요한 기본 수학적 개념을 소개한다.
- 먼저 응용수학의 기본적인 아이디어에서 시작한다.
- 많은 변수의 함수를 정의한다
- 함수의 최고점과 최저점을 찾는다
- quantify degrees of belief
- 다음으로 머신러닝 기본 목표를 설명한다.
- 특정 belief를 나타내는 모델을 지정한다
- 비용 함수를 디자인한다 : belief가 실제와 얼마나 잘 일치하는지를 측정
- 비용 함수를 최소화하는 학습 알고리즘을 사용한다
- 먼저 응용수학의 기본적인 아이디어에서 시작한다.
-
이러한 기본 프레임워크는 다양한 머신러닝 알고리즘의 기반이 된다. 다음 파트에서는 이러한 프레임워크 내에서의 딥러닝 알고리즘을 다룬다.
1장~6장 복습
TIMESTAMP
@200928 시작
- 책은 세 파트로 1장의 도입부를 시작하여 Part I은 2장 선형대수학, 3장 확률과 정보이론, 4장 수치해석, 5장 머신러닝 기초까지 다루며, Part II의 심층망에서 6장은 순방향네트워크를 다룬다.
1장 : 도입
- 1장은 도입으로, AI에서 사람이 직접 하드코딩하며 knowledge based approach이고 ML은 패턴을 추출하며 their own knowledge를 습득한다.
- 데이터의 representation은 머신러닝 성능을 좌우한다. ML 중에서도 representation learning을 사용해서 기존에 ML이 주어진 representation으로부터 output을 매핑하는 것 외에도 representation 자체를 찾도록 하였다 (예: 오토인코더)
- 데이터를 잘 설명하는 factors of variation을 분리해내고자 하며, ML에 적절한 representation을 줄 수 없다면 representation learning을 하거나, 혹은 DL을 통해 더욱 단순한 형태의 representation으로 만들어 이러한 문제를 해결할 수 있다.
- 딥러닝을 통해 적절한 representation을 학습하는 것 외에도 depth 측면에서 생각할 수 있다. 딥러닝은 특히 nested hierarchy of concepts를 가지고 있으며 더욱 더 단순화되거나 추상화된 형태로 개념을 구성하고 학습하여 좋은 성능을 보여준다.
- 첫번째 물결은 단순선형모델로, 입력값 과 출력값 에 대해서 가중치 을 학습하고 이에 따라 예측값 을 계산한다.
- 처음에는 무엇이 적절한 가중치인지 사람에 의해 지정되었다.
- 퍼셉트론의 활성함수는 값을 임계값을 기준으로 (+1,-1)로 분류하며, 실제값 (+1,-1)과 다를 경우 가중치를 업데이트한다.
- 아달라인의 활성함수는 와 실제값과의 차이를 비용함수 로 하며, 비용함수가 최소화되도록 경사하강법을 통해 가중치를 업데이트한다.
- 아달라인에서 사용된 SGD는 현대에서 사용되고 있으며, 퍼셉트론과 아달라인에 사용된 에 기반한 선형모형이 여전히 사용되고 있다.
- XOR 함수를 학습할 수 없는 등 선형모형은 많은 제한을 가진다.
- 두번째 물결에서는 distributed representation, back-propagation, LSTM이 나타난다.
- 세번째 물결에서는 '딥러닝'이 본격적으로 나오기 시작했으며, 이전보다 더 깊은 신경망을 훈련시킬 수 있으며 Depth의 이론적인 중요성이 대두되었다.
- 데이터셋이 증가되고, 모델 사이즈가 커졌으며, 뉴런의 갯수 또한 증가하였다.
2장 : 선형대수학
- 스칼라, 벡터, 행렬, 텐서
- 행렬의 전치, 행렬곱
- 고유값분해 : 고유벡터와 고유값
3장 : 확률과 정보이론
- 확률이론
- 정보이론
- 엔트로피, KL divergence
4장 : 수치 계산
Overflow and Underflow
- : 오버플로우를 해결하고 분모의 언더플로우를 해결
- 분자의 언더플로우는 여전히 문제이므로 계산을 안정화해야 한다.
Poor Conditioning
- condition number :
Gradient-based Optimization
- Gradient descent : objective function, criterion, cost function, loss function, error function
- Critical points : local minimum, local maximum, saddle points, global minimum
- Steepest descent : directional derivative, method of steepest descent, learning rate
- Jacobian matrix : 입력값과 출력값이 모두 벡터인 함수의 모든 편미분 행렬
- Curvature : second derivative
- Hessian matrix : Hessian is the Jacobian of the gradient
- Second derivative test
- 인 critical point에서 local maximum, local minimum, saddle point인지 결정하기 위해 행렬의 고유값을 확인할 수 있다.
- Newton's method
- 2차 테일러 급수를 이용하여 근처의 를 근사한다.
- 이 함수의 critical point에 대해 풀어보면 다음과 같다.
Constraint Optimization
5장 : 머신러닝 기초
Learning algorithms
- Task T, Performance P, Experience E
- Example: Linear regression
Capacity, Overfitting, Underfitting
- Generalization error
- Statistical learning theory
- No free lunch theorem
- Regularization
Hyperparameters and Validation sets
- Cross-validation
Estimators, Bias and Variance
- Point estimation
- Bias
- Variance and Standard error
- Trading off bias and variance to minimize mean squared error
- Consistency
Maximum likelihood estimation
- Conditional Log-Likelihood and Mean Squared Error
- Properties of Maximum Likelihood
Bayesian Statistics
- Maximum A Posteriori (MAP) Estimation
Supervised Learning Algorithm
- Probabilistic Supervised Learning
- Support Vector Machines
- Other Simple Supervised Learning Algorithms
Unsupervised Learning Algorithm
- Principal Components Analysis
- k-means Clustering
Stochastic Gradient Descent
Building a Machine Learning Algorithm
Challenges Motivating Deep Learning
- The Curse of Dimensionality
- Local Constancy and Smoothness Regularization
- Manifold Learning
6장 : 심층 순방향 네트워크
Example: Learning XOR
Gradient-Based Learning
- Cost Functions
- Learning Conditional Distributions with Maximum Likelihood
- Learning Conditional Statistics
- Output Units
- Linear Units for Gaussian Output Distributions
- Sigmoid Units for Bernoulli Output Distributions
- Softmax Units for Multinoulli Output Distributions
- Other Output Types
Hidden Units
- Rectified Linear Units and Their Generalizations
- Logistic Sigmoid and Hyperbolic Tangent
- Other Hidden Units
