[알고리즘] 정렬

---

1. 선택 정렬

---

---

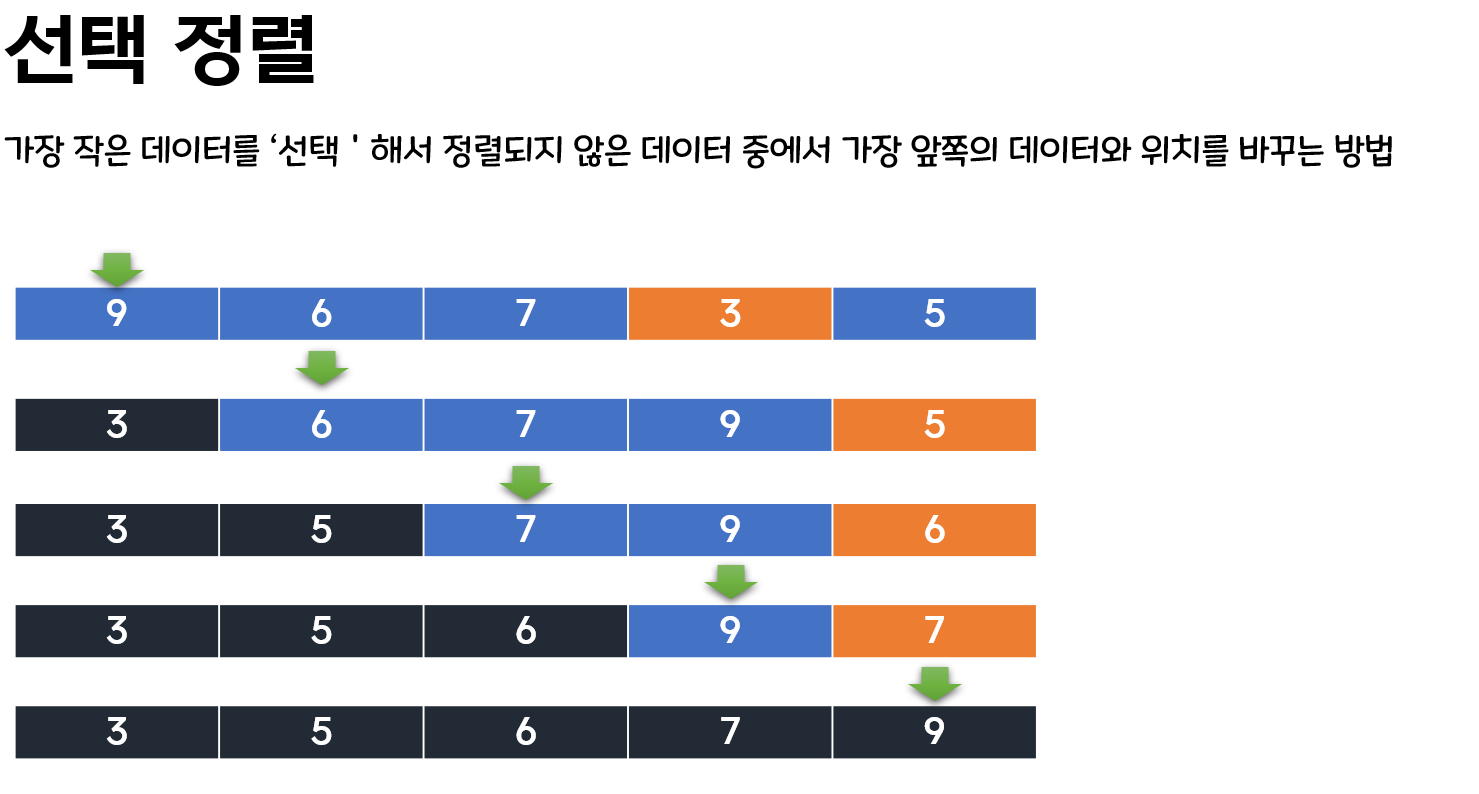
자바 코드

void selectionSort(int[] arr) {
    int indexMin, temp;
    for (int i = 0; i < arr.length-1; i++) {        // 바꾸려고 하는 위치 선정
        indexMin = i;
        for (int j = i + 1; j < arr.length; j++) {  // 배열을 순회하며 기준위치 보다 낮은 원소를 탐색
            if (arr[j] < arr[indexMin]) {           // 최저값이 나올때마다 갱신
                indexMin = j;
            }
        }
        temp = arr[indexMin];						// 값을 바꿔줌
        arr[indexMin] = arr[i];
        arr[i] = temp;
  }
  System.out.println(Arrays.toString(arr));
}

---

시간 복잡도

N개의 데이터를 정렬한다고 했을 때

• 첫 번째 루프 : N-1 번 비교 ( index 1 ~ index N-1 )
• 두 번째 루프 : N-2 번 비교 ( index 2 ~ index N-1 )
  . . .
• (n-1) + (n-2) + . . . + 2 + 1 = n(n-1)/2

  선택 정렬의 시간 복잡도는 $O(N^2)$ 이다 .

---

공간 복잡도

주어진 배열 내에서만 정렬이 이루어 지기 때문에 $O(1)$ 이다.

선택 정렬의 공간 복잡도는 $O(1)$ 이다.

---

2. 삽입 정렬

---

---

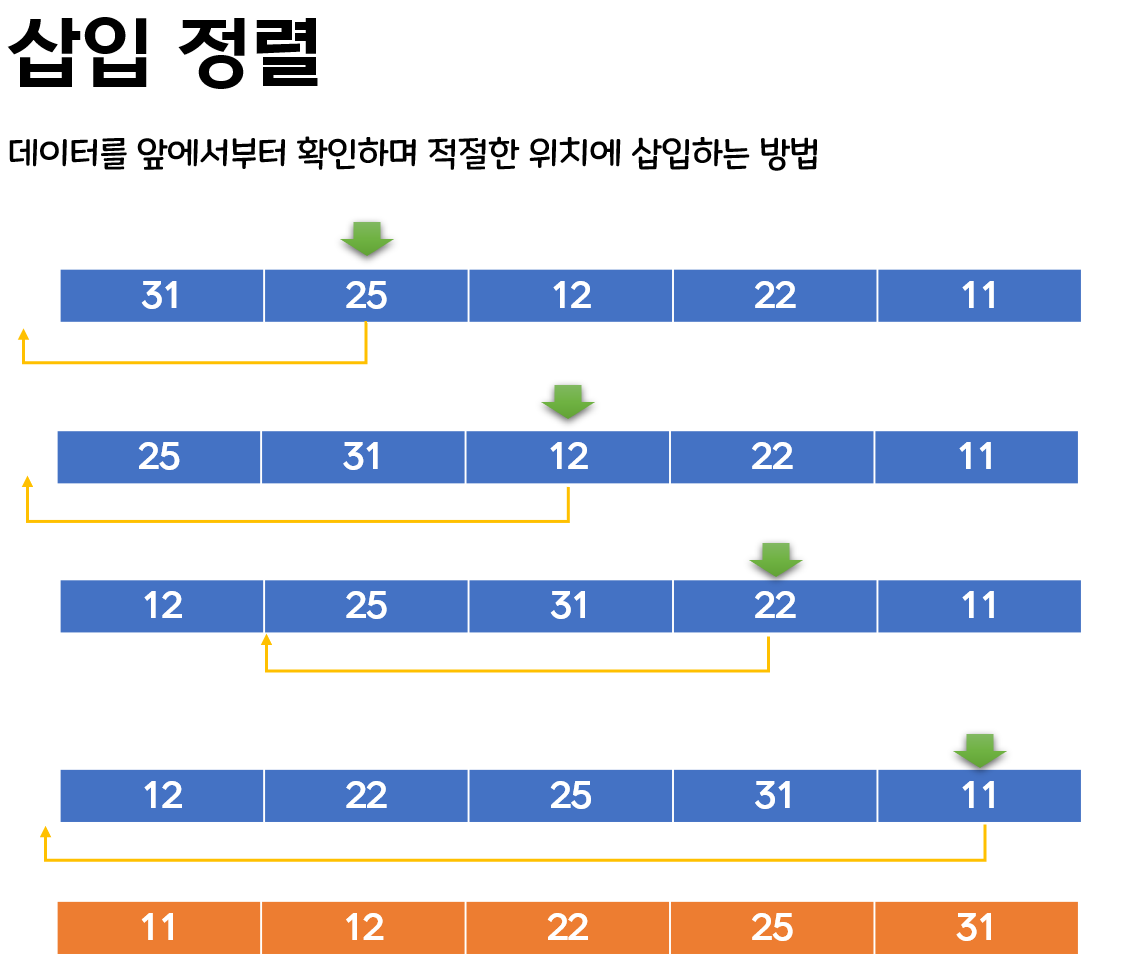
자바 코드

void insertionSort(int[] arr)
{

   for(int index = 1 ; index < arr.length ; index++){

      int temp = arr[index];
      int aux = index - 1;

      while( (aux >= 0) && ( arr[aux] > temp ) ) {

         arr[aux+1] = arr[aux];
         aux--;
      }
      arr[aux + 1] = temp;
   }
}

---

시간 복잡도

N개의 데이터를 정렬한다고 했을 때

삽입 정렬의 시간 복잡도는 $O(N^2)$ 이다 .

---

공간 복잡도

주어진 배열 내에서만 정렬이 이루어 지기 때문에 O(1) 이다.

삽입 정렬의 공간 복잡도는 $O(1)$ 이다.

---

3. 퀵 정렬

---

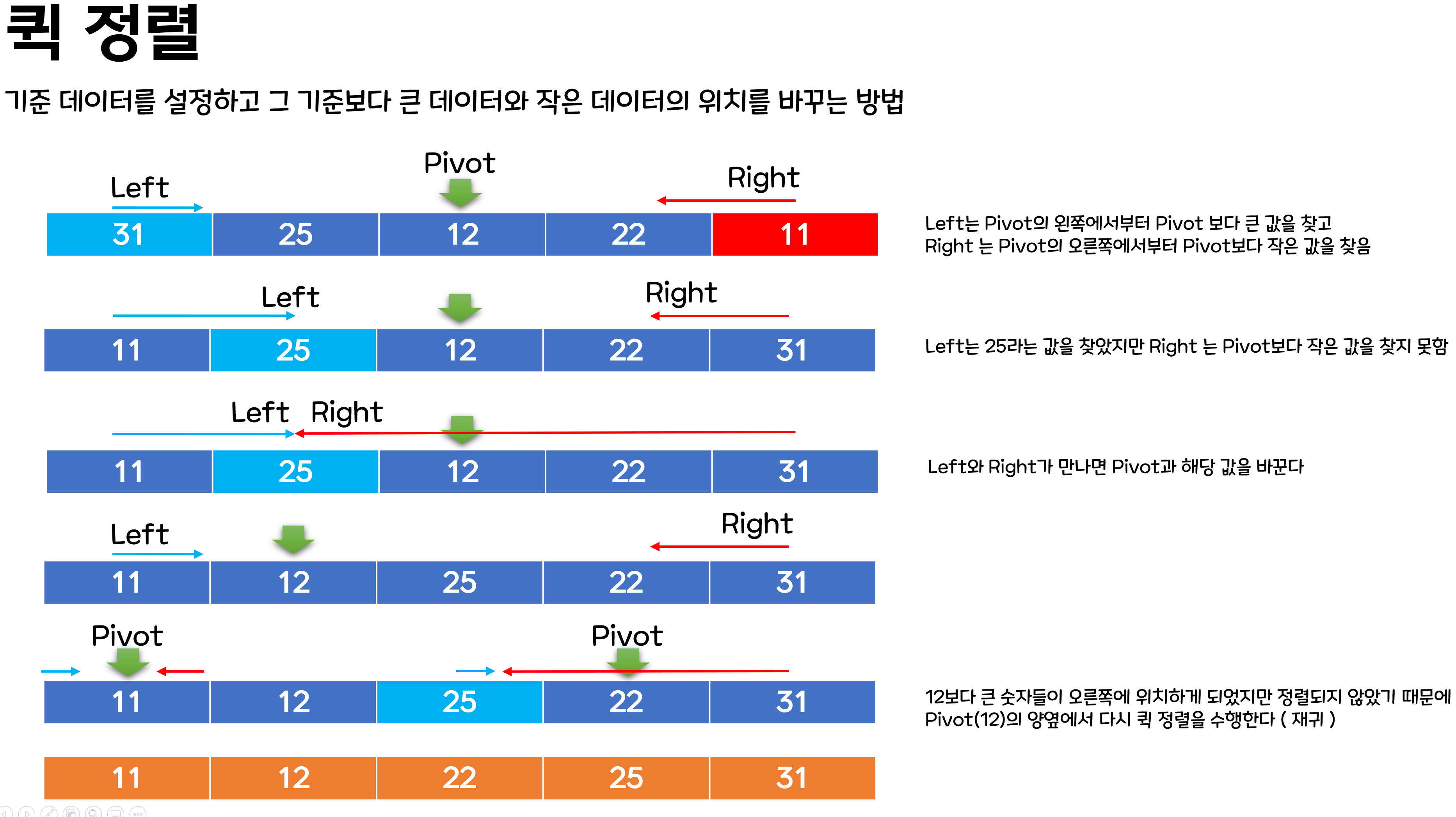
자바 코드

public void quickSort(int[] arr, int left, int right) {
    int i, j, pivot, tmp;
    if (left < right) {
        i = left;   j = right;
        pivot = arr[(left+right)/2];
        //분할 과정
        while (i < j) {
            while (arr[j] > pivot) j--;
            // 이 부분에서 arr[j-1]에 접근해서 익셉션 발생가능함.
            while (i < j && arr[i] < pivot) i++;

            tmp = arr[i];
            arr[i] = arr[j];
            arr[j] = tmp;
        }
        //정렬 과정
        quickSort(arr, left, i - 1);
        quickSort(arr, i + 1, right);
    }
}

---

시간 복잡도

공부한 결과 퀵 정렬은 논리는 똑같지만 사람들 마다 구현하는 방법의 차이가 있었다. 그중 Pivot을 다양한 방법으로 설정하는 사람들이 있었는데 Pivot을 가장 처음으로 잡게 될 경우 worst case(이미 정렬되어있는 경우) 에서 성능이 저하된다. Pivot을 가운데 인덱스로 설정함으로써 최악의 경우를 피할 수 있다.

삽입 정렬의 시간 복잡도는 $O(NlogN)$ 이다 .

---

공간 복잡도

주어진 배열 내에서만 정렬이 이루어 지기 때문에 O(1) 이다.

삽입 정렬의 공간 복잡도는 $O(1)$ 이다.

---

4. 계수 정렬

---

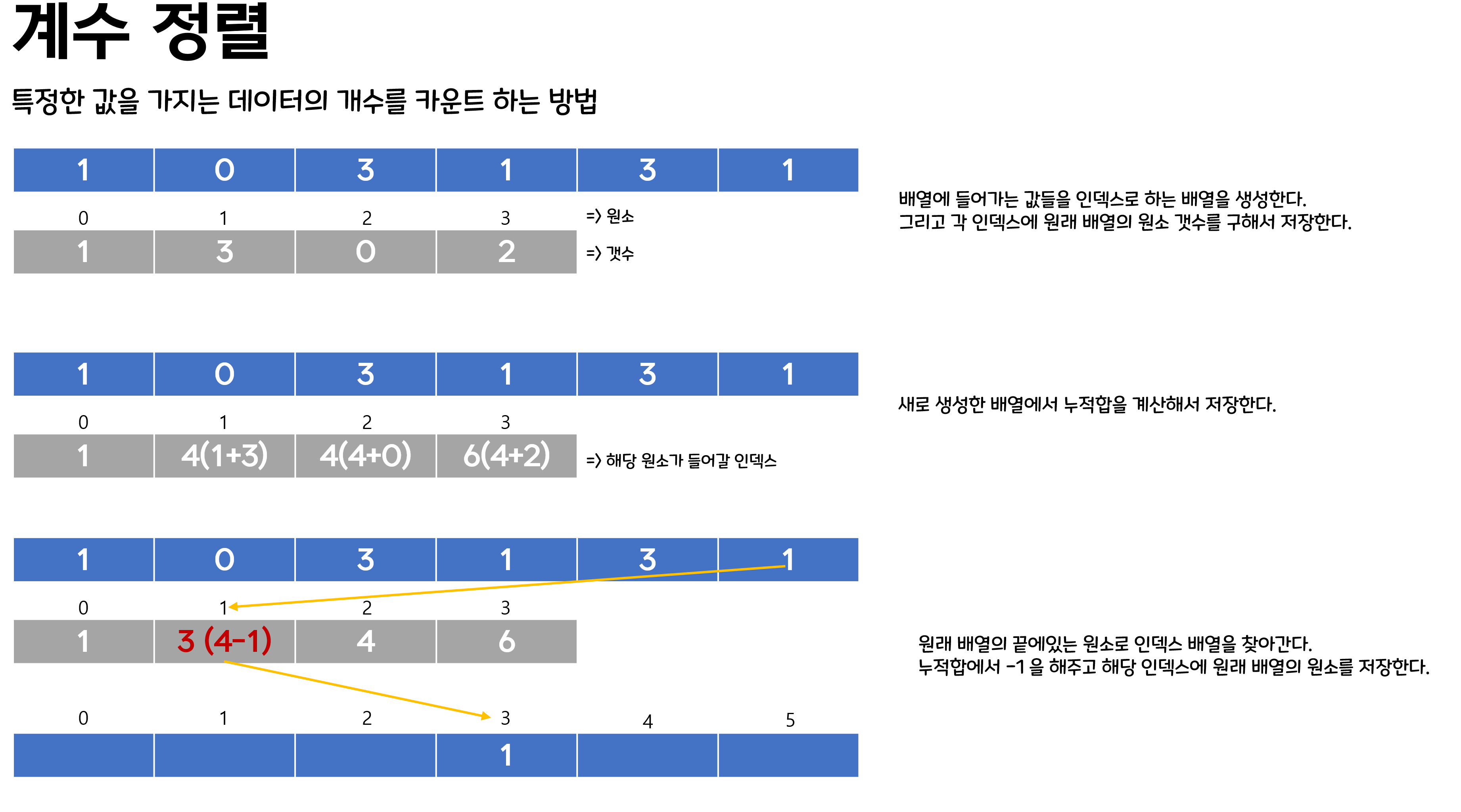
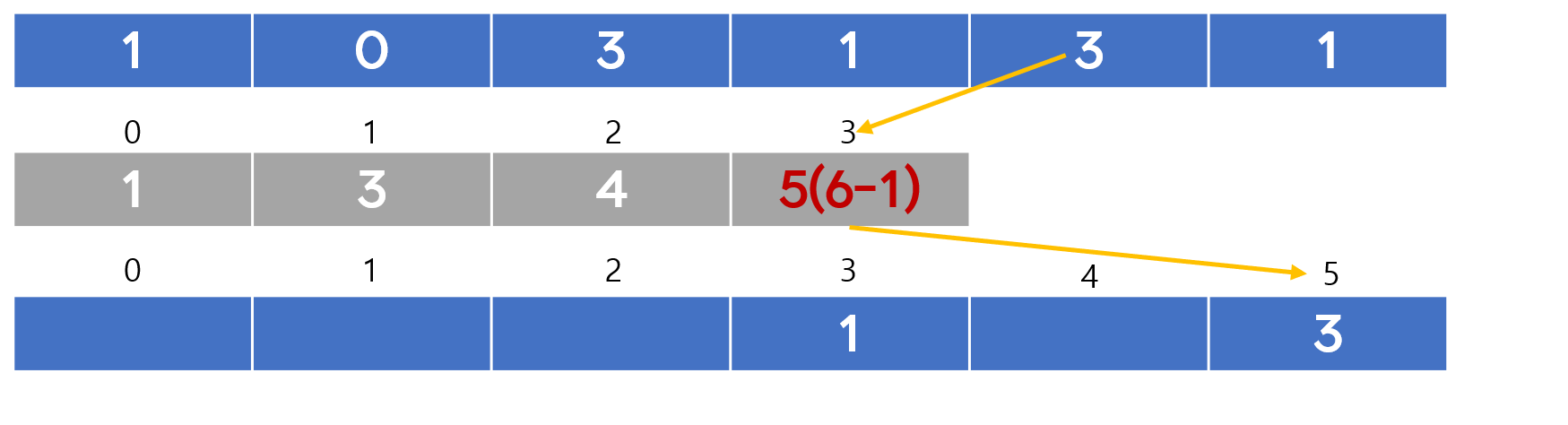
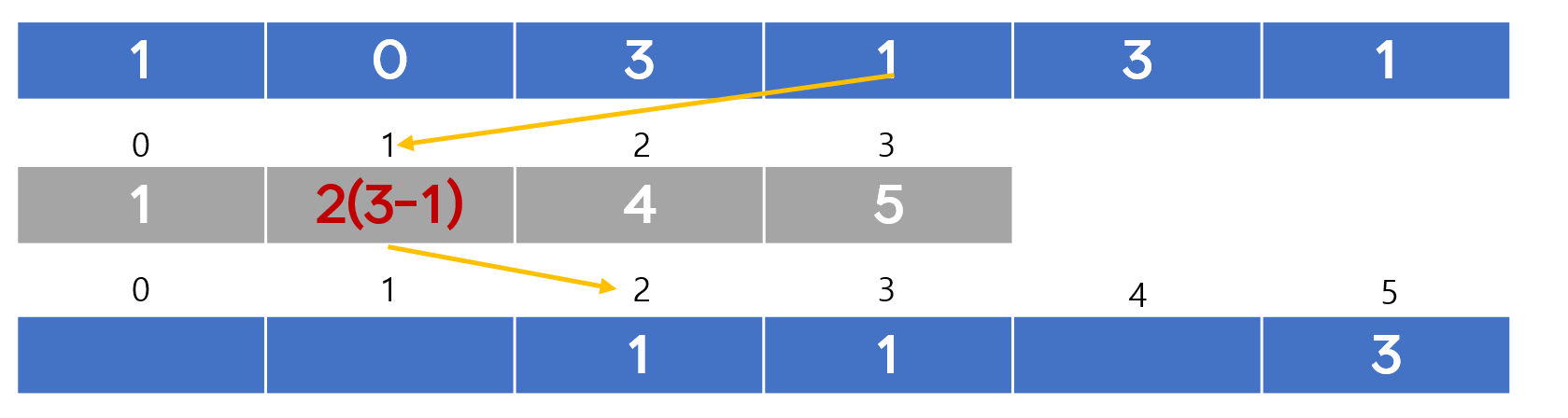
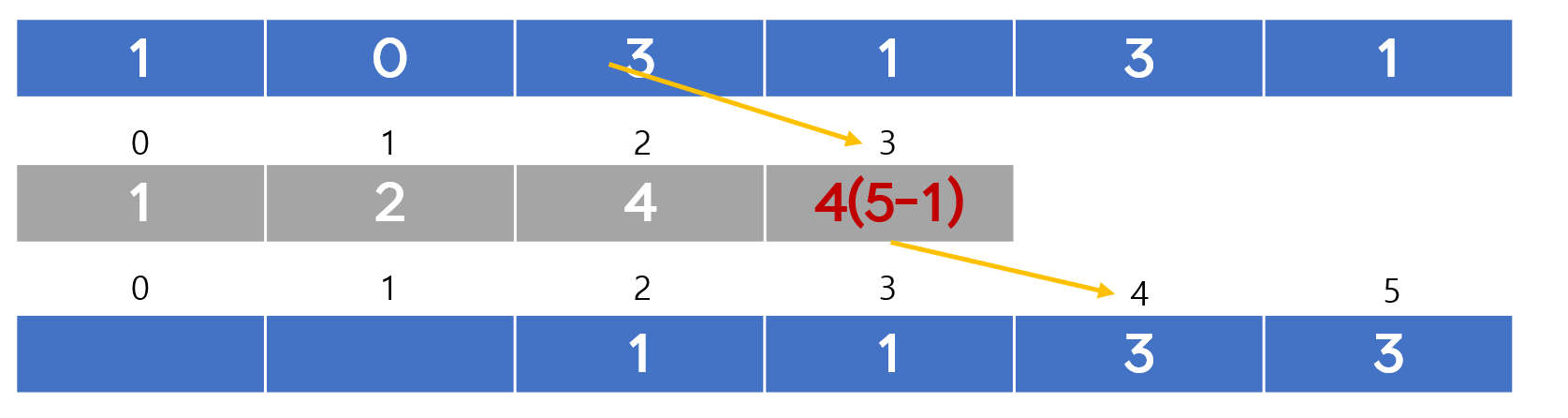
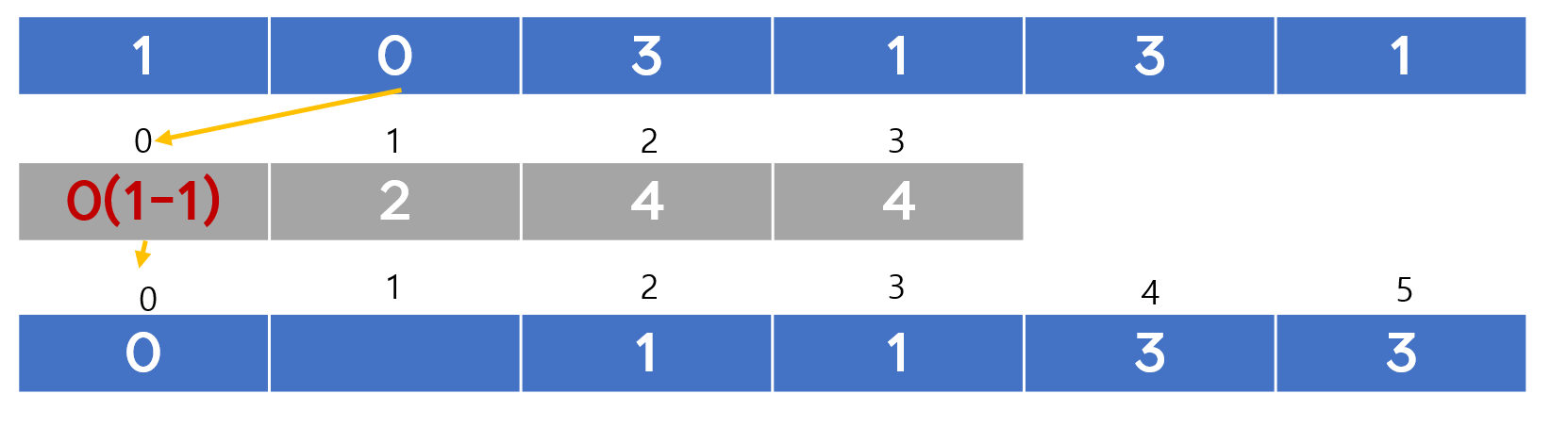
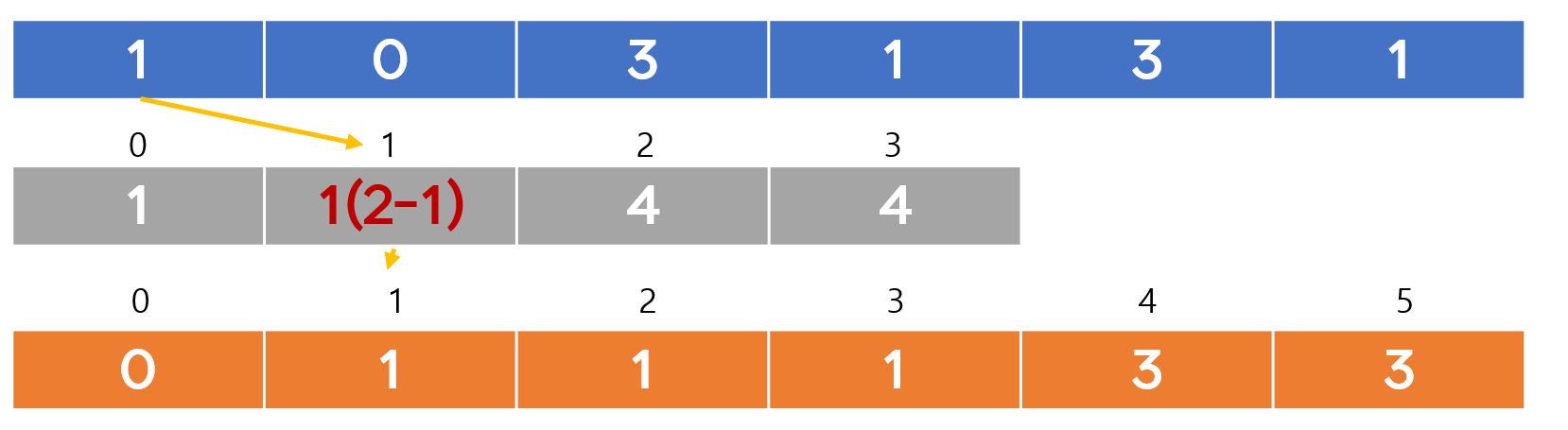
자바 코드

package Algorithm;

import java.util.Arrays;
import java.util.Random;

public class CountingSort {

    static final int N = 10;

    public static void main(String[] args) {
        Random random = new Random(); // 랜덤함수를 이용

        int[] arr = new int[N];
        for (int i = 0; i < N; i++) {
            arr[i] = random.nextInt(100); // 0 ~ 99
        }

        System.out.println("정렬 전: " + Arrays.toString(arr));
        countingSort(arr);
        System.out.println("정렬 후: " + Arrays.toString(arr));
    }

    private static void countingSort(int[] arr) {
        // 최대값 구하기
        int max = arr[0];
        for (int i = 1; i < arr.length; i++) {
            if (max < arr[i])
                max = arr[i];
        }

        int[] counting = new int[max + 1]; // 카운팅 배열

        for (int i = 0; i < N; i++) {
            counting[arr[i]]++;
        }

        int index = 0;
        for (int i = 0; i < counting.length; i++) {
            while (counting[i]-- > 0) {
                arr[index++] = i;
            }
        }
    }
}

---

시간 복잡도

계수 정렬의 경우 데이터의 크기가 한정되어 있는 경우에만 사용이 가능하지만 상당히 빠르게 동작한다. 하지만 음수나 실수는 정렬하지 못한다는 단점이 있다.

계수 정렬의 시간 복잡도는 $O(N+K)$ 이다 . (K는 데이터 중에서 가장 큰 양수)

---

공간 복잡도

계수 정렬의 공간 복잡도는 $O(N+K)$ 이다.

---

5. 버블 정렬

---

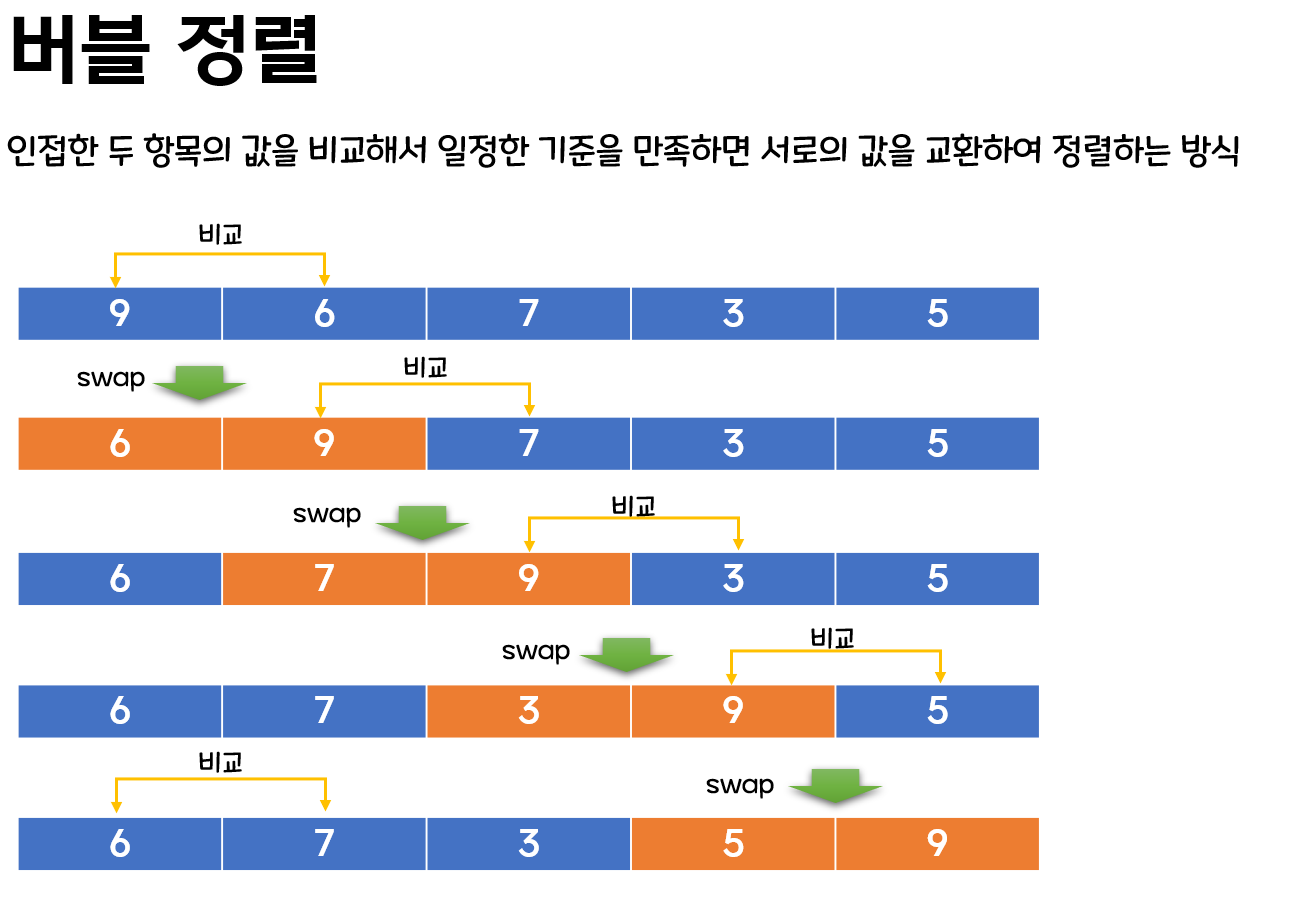
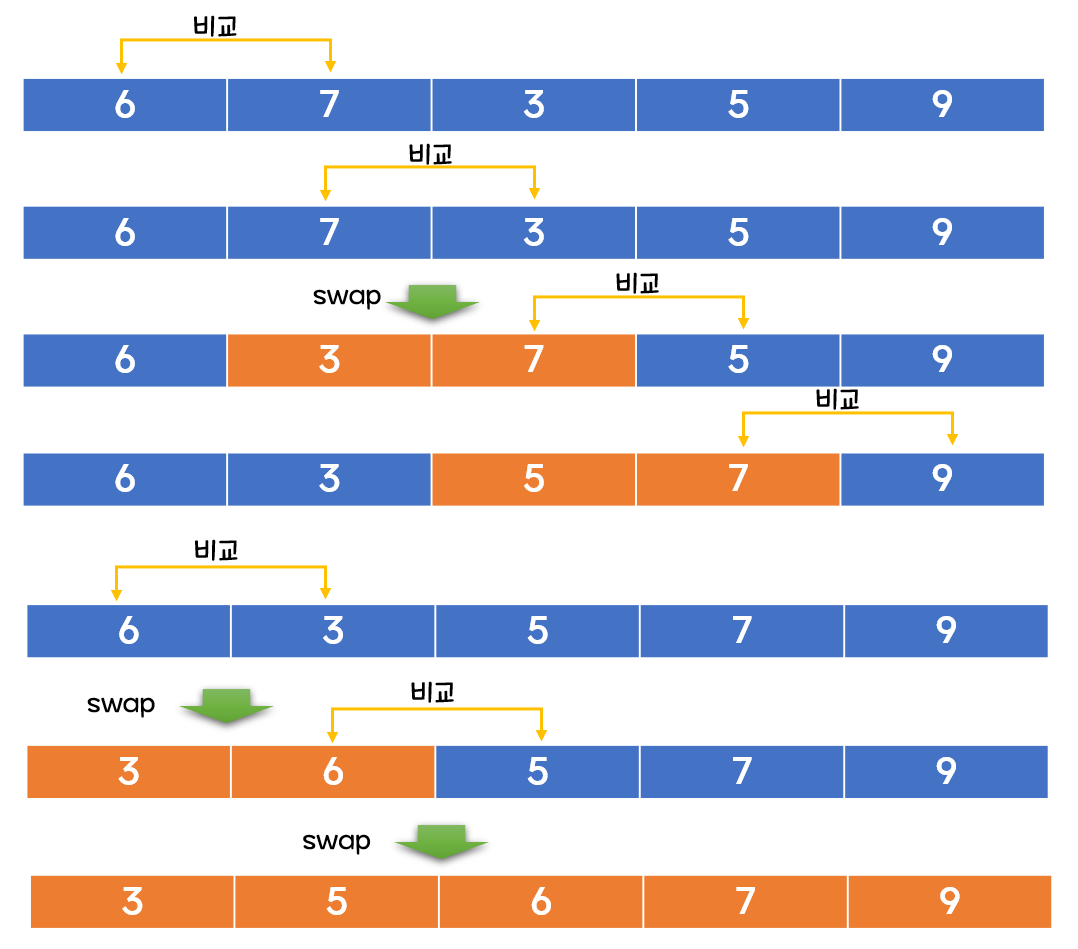
자바 코드

void bubbleSort(int[] arr) {
    int temp = 0;
	for(int i = 0; i < arr.length - 1; i++) {
		for(int j= 1 ; j < arr.length-i; j++) {
			if(arr[j]<arr[j-1]) {
				temp = arr[j-1];
				arr[j-1] = arr[j];
				arr[j] = temp;
			}
		}
	}
	System.out.println(Arrays.toString(arr));
}

---

시간 복잡도

버블 정렬의 시간 복잡도는 $O(N^2)$ 이다 .

---

공간 복잡도

버블 정렬의 공간 복잡도는 $O(1)$ 이다.

---

---

6. 힙 정렬

---

출처

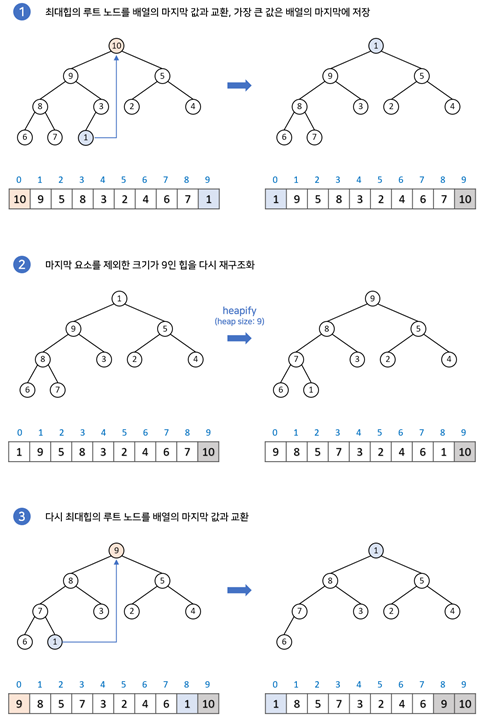
엄청 느리지만 힙 정렬되는 과정을 잘 보여준다. (출처)

자바 코드

public class Heap
{
	private int[] element; //element[0] contains length
	private static final int ROOTLOC = 1;
	private static final int DEFAULT = 10;

	public Heap(int size) {
		if(size>DEFAULT) {element = new int[size+1]; element[0] = 0;}
		else {element = new int[DEFAULT+1]; element[0] = 0;}
	}

	public void add(int newnum) {

		if(element.length <= element[0] + 1) {
			int[] elementTemp = new int[element[0]*2];
			for(int x = 0; x < element[0]; x++) {
				elementTemp[x] = element[x];
			}
			element = elementTemp;
		}
		element[++element[0]] = newnum;
		upheap();
	}

	public int extractRoot() {
		int extracted = element[1];
		element[1] = element[element[0]--];
		downheap();
		return extracted;
	}

	public void upheap() {
		int locmark = element[0];
		while(locmark >= 1 && element[locmark/2] > element[locmark]) {
			swap(locmark/2, locmark);
			locmark /= 2;
		}
	}

	public void downheap() {
		int locmark = 1;
		while(locmark * 2 <= element[0])
		{
			if(locmark * 2 + 1 <= element[0]) {
				int small = smaller(locmark*2, locmark*2+1);
				swap(locmark,small);
				locmark = small;
			}
			else {
				swap(locmark, locmark * 2);
				locmark *= 2;
			}
		}
	}

	public void swap(int a, int b) {
		int temp = element[a];
		element[a] = element[b];
		element[b] = temp;
	}

	public int smaller(int a, int b) {
		return element[a] < element[b] ? a : b;
	}
}

---

시간 복잡도

$(log n+log(n-1)+...+log2)$

$=(log n+log(n-1)+...+log 2)+(log n+log(n-1)+...+log 2)$
$=(log n+log(n-1)+...+log 2)+(log n+log(n-1)+...+log 2)$

$= (n\log n)$

힙 정렬의 시간 복잡도는 $O(Nlog N)$ 이다 .

---

공간 복잡도

힙 정렬의 공간 복잡도는 $O(1)$ 이다.

---

---

7. 합병 정렬

---

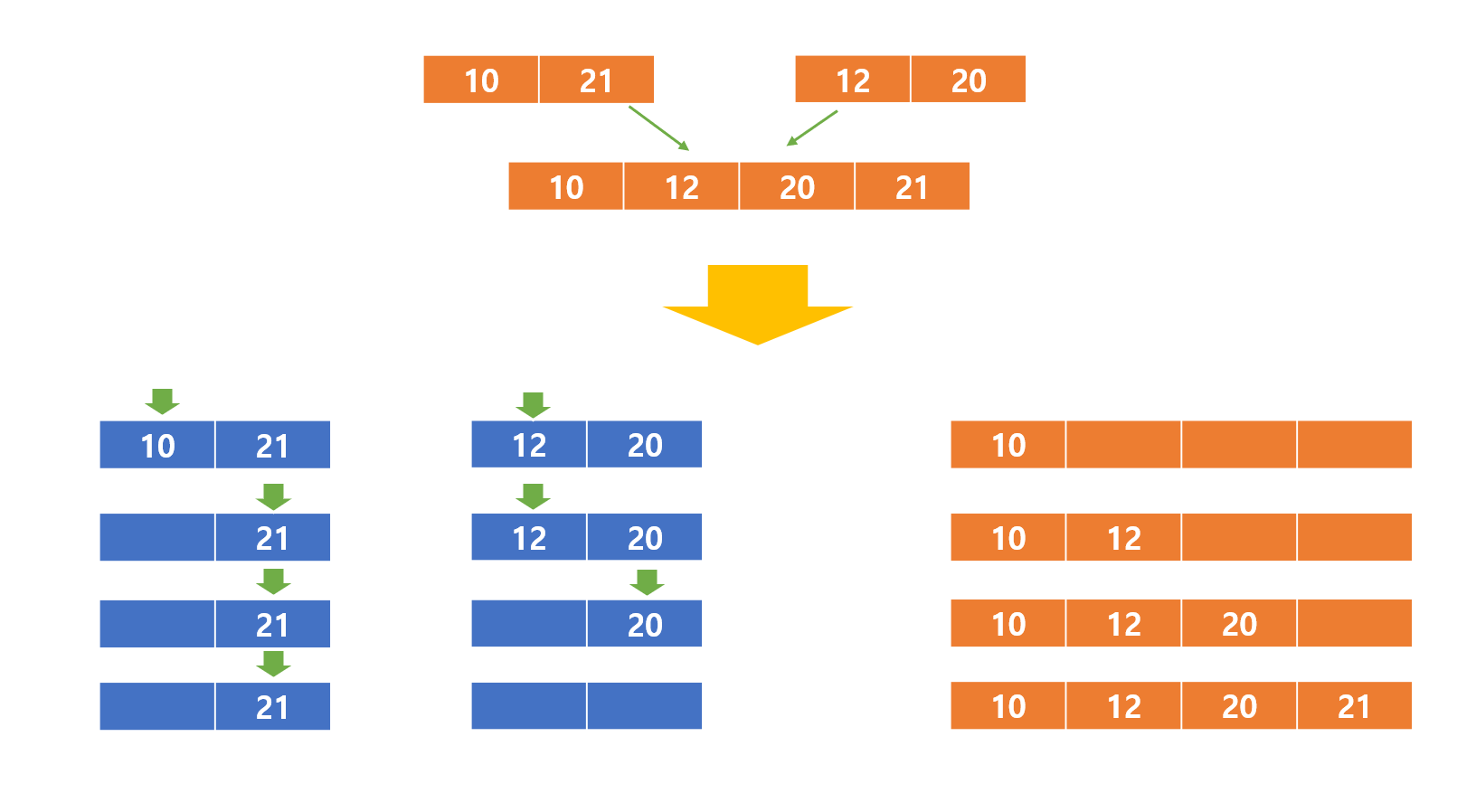
자바 코드

public class Main {
	public static int[] src;
	public static int[] tmp;

	public static void main(String[] args) {
		src = new int[] { 1, 9, 8, 5, 4, 2, 3, 7, 6 };
		tmp = new int[src.length];
		printArray(src);
		mergeSort(0, src.length - 1);
		printArray(src);
	}

	public static void mergeSort(int start, int end) {
		if (start < end) {
			int mid = (start + end) / 2;
			mergeSort(start, mid);
			mergeSort(mid + 1, end);
			int p = start;
			int q = mid + 1;
			int idx = p;
			while (p <= mid || q <= end) {
				if (q > end || (p <= mid && src[p] < src[q])) {
					tmp[idx++] = src[p++];
				} else {
					tmp[idx++] = src[q++];
				}
			}
			for (int i = start; i <= end; i++) {
				src[i] = tmp[i];
			}
		}
	}

	public static void printArray(int[] a) {
		for (int i = 0; i < a.length; i++)
			System.out.print(a[i] + " ");
		System.out.println();
	}
}
//출처 : https://yunmap.tistory.com/entry/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Java%EB%A1%9C-%EA%B5%AC%ED%98%84%ED%95%98%EB%8A%94-%EC%89%AC%EC%9A%B4-Merge-Sort-%EB%B3%91%ED%95%A9-%EC%A0%95%EB%A0%AC-%ED%95%A9%EB%B3%91-%EC%A0%95%EB%A0%AC

---

시간 복잡도

합병 정렬의 시간 복잡도는 $O(Nlog(N))$ 이다 .

---

공간 복잡도

합병 정렬의 공간 복잡도는 $O(N)$ 이다.

---

총 정리

정렬알고리즘	평균 시간 복잡도	공간 복잡도	특징
선택정렬	$O(N^2)$	$O(1)$	아이디어가 매우 간단하다.
삽입 정렬	$O(N^2)$	$O(1)$	데이터가 거의 정렬되어 있을때 가장 빠르다
버블 정렬	$O(N^2)$	$O(1)$	구현이 매우 간단하다.
퀵 정렬	$O(NlogN)$	$O(1)$	대부분의 경우에 가장 적합하며, 충분히 빠르다
힙 정렬	$O(NlogN)$	$O(1)$	최악의 경우에도$O(NlogN)$를 갖는다
합병 정렬	$O(NlogN)$	$O(N)$	최악의 경우에도$O(NlogN)$를 갖는다
계수 정렬	$O(N+K)$	$O(N+K)$	한정적인 상황에 사용 가능하지만 매우 빠르다

출처 : https://herong.tistory.com/entry/%EA%B3%84%EC%88%98%EC%A0%95%EB%A0%ACCounting-Sort