3dgs projection 수식

chaenyang·2025년 7월 2일

3D

목록 보기

9/9

3D gaussian을 2D image plane에 projection하는 과정이다.

\Sigma' = JW \Sigma W^{T} J^{T}

Jacobian은 affine projection할 때 쓰는 행렬이다.

일단 affine projection이 뭔지 이해를 해보면

3D 상에 좌표 P(x, y, z)가 있다 할 때 이 좌표를 2D로 나타낼 때 image plane 위에 projection 해야한다. 이때 카메라 원점과 P를 이으면 image plane과 만나는 점이 생기는데 이 지점이 projection되는 곳이다.

Image plane은 z = 1인 곳에 있으므로 2D에서 P의 좌표는 $(x', y') = (\frac{x}{z}, \frac{y}{z})$ 가 된다.

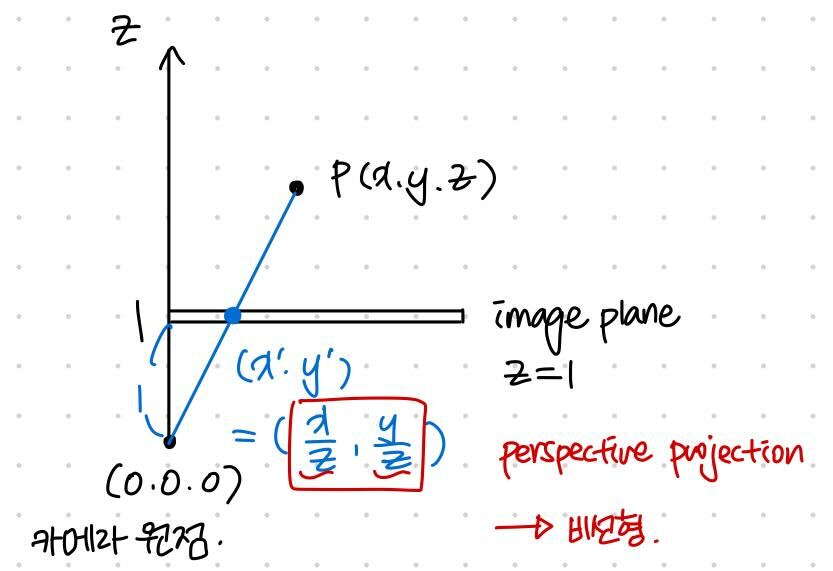
이때 z로 나누기 때문에 비선형 변환이 일어난다. z가 크면 화면에서 작게 보이고 z가 작으면 화면에서 크게 보여서 원근 효과가 일어난다.

f(x, y, z) = \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \frac{x}{z} \\ \frac{y}{z} \end{bmatrix}

수식으로 나타내면 위와 같다.

따라서 perspective(원근) projection이 일어난다고 할 수 있는데 이는 비선형 변환이다.

비선형 변환은 연산이 복잡하기 때문에 선형으로 근사를 해줘야하는데, perspective projection을 선형으로 단순화하는게 affine 변환이다.

이때 affine projection을 하기 위해 사용하는 행렬이 Jacobian이다.

Jacobian은 입력에 따라 출력이 어떻게 변하는지 나타낸다. 3D 위치 변화가 2D 위치에 어떤 영향을 주는지를 선형 근사한 것이다.

따라서 output을 input으로 편미분해주면 된다.

수식으로 설명해보자면

f(x, y, z) = \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \frac{x}{z} \\ \frac{y}{z} \end{bmatrix}

J = \begin{bmatrix} \frac{\partial x'}{\partial x} & \frac{\partial x'}{\partial y} & \frac{\partial x'}{\partial z} \\ \frac{\partial y'}{\partial x} & \frac{\partial y'}{\partial y} & \frac{\partial y'}{\partial z} \end{bmatrix} = \begin{bmatrix} \frac{1}{z} & 0 & -\frac{x}{z^2} \\ 0 & \frac{1}{z} & -\frac{y}{z^2} \end{bmatrix}

output을 input으로 각각 나눠주면 Jacobian 행렬이 된다.

잉공지능