Generative Model이란?

Generative model(생성 모델)은 데이터의 분포를 학습하여 새로운 데이터를 생성하는 모델이다. Generative model의 주요 목표는 주어진 데이터의 확률 분포 $p(x)$를 학습하는 것이다. 이를 통해 1) 새로운 데이터 샘플을 생성하거나(Generation), 2) 주어진 데이터의 가능성을 평가(Density estimation)할 수 있다.

Generative Model의 주요 기능

1. Generation (생성)

• 모델이 학습한 확률분포 $p(x)$에서 샘플링하여 새로운 데이터를 생성한다.
• 예를 들어, 모델이 강아지 이미지를 학습했다면, $x ~ p(x)$를 샘플링하여 새로운 강아지 이미지를 생성한다.
  • (참고) 확률분포에서의 샘플링이란 무엇인가?
    확률 분포에서 샘플을 생성한다는 것은 주어진 확률 분포를 따르는 랜덤한 값(샘플)을 생성하는 것을 의미한다. 이는 특정 확률 분포에 의해 결정된 확률에 따라 데이터를 무작위로 선택하거나 생성하는 과정이다.

2. Density Estimation (밀도 추정)

• 모델이 주어진 데이터 $x$에 대해 확률밀도 $p(x)$를 평가한다.
• 주어진 데이터 x가 실제로 강아지 사진 같은지 판단하는 것을 의미한다. 이런 모델을 explicit models라고 한다.
  • 이 때 만약 x가 강아지 이미지 같다면 $p(x)$가 1에 가까운 큰 값이 output될 것이다.
  • 즉, 이 기능은 주어진 데이터가 해당 분포에 속할 확률을 평가하는 데에 사용된다.

그렇다면 $p(x)$를 어떻게 구할까?

확률 분포 모델링 방법

1) 이산 확률 분포 (Discrete Distributions)

개념 및 한계

이 방법론의 문제는 모델을 구축할 때 너무 많은 파라미터가 필요하다는 것이다. 예를 들어, 카테고리 분포는 $\sum_{i=1}^{m}p_{i} = 1$ (주사위 예시라면 m = 6) 식을 따른다. 이 경우, (m-1)개의 파라미터가 필요하게 된다. RGB 이미지로 넘어가게 되면 얼마나 많은 파라미터가 필요하게 될지...

파라미터 수가 중요한 이유는 모델의 복잡도가 파라미터의 수에 의해 결정되기 때문이다. 더욱이 파라미터 수가 많을수록 과적합(overfitting)의 위험이 커지게 된다.

예시

RGB이미지에서 오직 한 픽셀을 모델링한다고 해보자.
R,G,B각각 0~255까지의 숫자 중 하나를 지니게 된다. 즉, R,G,B 각각 256개의 가능성이 있는 것이다.
여기까진 okay. 이 다음부터는 내가 처음 이해를 못했던 부분이다.

확률분포와 파라미터 수
확률분포를 사용하여 픽셀값을 모델링한다면, 확률분포 $p(x)$는 가능한 모든 픽셀 조합 $x$에 대해 확률을 할당한다.

이 때, 모든 가능한 픽셀 값 조합에 대한 확률의 합은 1이 되어야 된다. 즉, $\sum_{i=1}^{256*256*256}p(x_{i}) = 1$ 이다.

이제 파라미터 수를 계산해보자. 각 가능한 픽셀 값 조합에 대해 독립적인 확률 값을 할당하려면 256 x 256 x 256개의 확률 값을 정의해야 한다. 그러나 확률의 합이 1이 되어야 한다는 제약 조건이 있기 때문에, 256 x 256 x 256개의 확률 값 중 하나는 나머지 확률 값들에 의해 결정된다. 따라서 독립적으로 필요한 파라미터 수는 256 x 256 x 256 - 1개가 됩니다.

2) 독립성(Indepence) 가정

개념

앞에서 살펴보았듯, 카테고리 분포는 너무 많은 파라미터를 필요로 한다. 우리는 파라미터 수를 줄일 필요가 있다. 그 첫번째 방법은 독립성 가정, 즉, 각 변수가 서로 독립적으로 발생한다고 가정하는 것이다. 이렇게 되면, 파라미터 수를 줄여 모델을 단순화하고 계산을 용이하게 한다는 장점이 있다.

독립성 가정이 들어간다면, 확률분포 식은 다음과 같다.
$P(X_{1}, ..., X_{n}) = P(X_{1})P(X_{2})...P(X_{n})$

예시

1) 비교군을 위해 이산확률분포로 푸는걸 다시 해보자.
하나의 픽셀이 0과 1만 가지는 흑백 이미지이며, 크기가 28x28인 이미지(n=784)라고 해보자.

즉, 파라미터 수가 $2^{784}-1$만큼 필요하다는 것이다. 참고로, 최소한 데이터 수가 파라미터 수보다 많아야 한다. 데이터 수가 학습하고자 하는 파라미터 수보다 적으면 학습이 잘 안되기 때문이다. 즉, 엄청 많은 데이터가 필요하고 이렇게 하는건 거의 불가능한 일이다.

2) 이제 독립성 가정을 갖고 같은 문제를 다시 풀어보자.

(참고) 왜 파라미터수가 n인가?

• 각 픽셀은 1이 될 확률 $p_{i}$와 0이 될 확률 1-$p_{i}$를 가진다.
• 각 픽셀이 독립적이므로 각 픽셀의 확률은 다른 픽셀의 확률과 독립적으로 계산된다.

한계

이러한 독립성 가정은 기계학습 분야에서 표현력을 줄이기 위해 많이 사용된다. 그러나 의미있는 숫자/이미지를 얻어낼 수 없다는 한계가 있다. 예를 들어, 각 픽셀이 독립적이라면 절대 원하는 모양이 생성될 수가 없을 것이다.

즉, 우리는 온전한 독립성과 독립성이 아예 없어서 파라미터 수가 너무 많은 그 두 경우 사이의 무언가를 원한다.

3) 조건부 독립성 (Conditional Independence)

개념

조건부 독립성(Conditional Independence)란, 두 확률 변수가 세번째 변수 값이 주어졌을 때 서로 독립임을 의미한다.
즉, 조건부 독립성은 "제3의 변수 𝑍를 알게 되면 𝑋와 𝑌가 서로 영향을 주지 않는다"는 의미다. 다시 말해, 𝑍의 값이 주어졌을 때, 𝑋와 𝑌의 결합 확률은 각자의 조건부 확률의 곱으로 분리될 수 있다.
$P(X,Y|Z) = P(X|Z) * P(Y|Z)$

또는, 𝑋와 𝑌가 𝑍가 주어졌을 때 독립이라는 것을 표현하는 기호로 다음과 같이 표시하기도 한다: $X⊥Y∣Z$

마르코브 가정 (Markov Assumption)

마르코프 가정은 시퀀스나 연속적인 사건들에서 특정 상태가 이전 상태들에만 의존하고, 그 이전의 모든 상태들과는 독립임을 의미한다. 이는 다음 상태가 오직 현재 상태에만 의존하고, 그 이전의 모든 상태와는 독립이라는 것을 나타낸다.

예시

앞의 28x28 흑백 이미지에서 Markov 가정을 더한다면 총 필요한 파라미터 수가 어떻게 될까?

즉, fully independence보다는 크고 independence조건이 없는 것보다는 작다.
=> conditional independence는 그 사이 어딘가이다!

4) 자기회귀 모델 (Autoregressive Models)

개념

자기회귀 모델은 현재 시점의 데이터가 이전 시점의 데이터들의 선형 결합으로 표현될 수 있다는 가정에 기반한다. 예를 들어, 내일 날씨 예측을 위해 오늘과 어제의 날씨를 활용하는 것을 연속하는 것을 의미한다.
$X_{t} = \phi_{1}X_{t-1} + \phi_{2}X_{t-2} + ... + \phi_{p}X_{t-p} + \epsilon_{t}$

• $X_{t}$는 시간 t에서의 관측값.
• $\phi_{1}, \phi_{2}, ..., \phi_{p}$는 모델의 파라미터.
• $\epsilon_{t}$는 평균이 0이고 분산이 일정한 백색 잡음(white noise)

(참고) 왜 갑자기 자기회귀 모델?
자기회귀 모델은 마르코브 성질과도 연결된다. 1차 자기회귀 모델 (AR(1))의 경우, 현재의 값이 오직 바로 이전 값에만 의존하는 형태로, 이는 마르코브 가정의 특수한 경우(1차 마르코브 가정)이기 때문이다.
AR(1)의 식은 다음과 같다. $X_{t} = \phi X_{t-1} + \epsilon_{t}$ 즉, $X_{t}$는 $X_{t-1}$에만 의존한다.

5) NADE (Neural Autoregressive Density Estimator)

개념

이 부분은 다음 블로그 https://velog.io/@dldydldy75/Generative-Models-%EA%B8%B0%EB%B3%B8 의 도움을 많이 받았고, 해당 내용을 정리한 것이다.

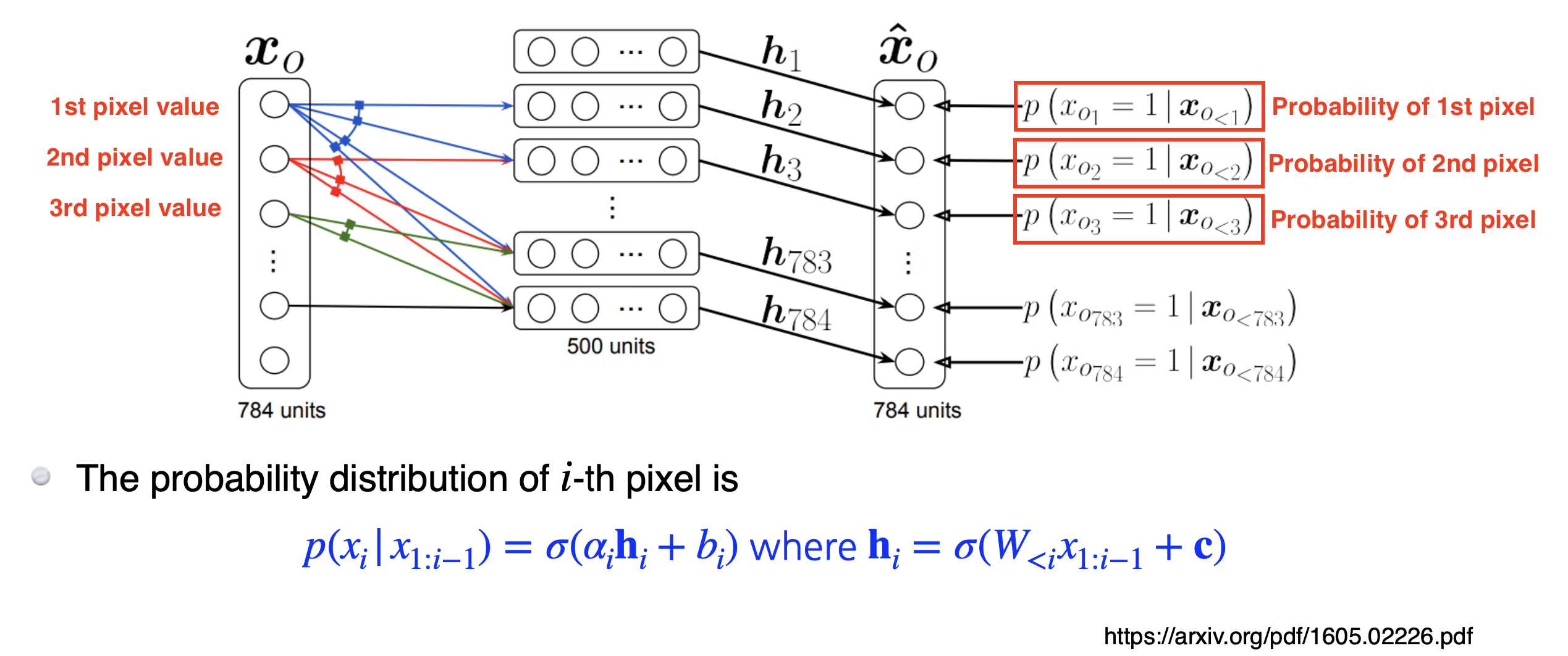
NADE는 Autoregressive model을 Neural Network/Deep Learning에 처음 접목한 논문이다. NADE의 내용은 다음과 같다.

i 번째 픽셀을 1 ~ i-1 번째 픽셀에 의존하게 만든다.
첫 번째 픽셀의 확률분포는 독립적으로 만들고, 두 번째 픽셀의 확률은 첫 번째 픽셀에 의존 (h 가 됨), 세 번째 픽셀의 확률은 첫 번째와 두번째에 의존 ...하는 방식으로 끝까지 진행된다. 즉, 100번째 뉴럴 네트워크 (100번째 픽셀에 대한 확률분포) 만들 때는 99 개의 이전 입력들을 받을 수 있는 뉴럴 네트워크 필요한 것이다.
출처: https://velog.io/@dldydldy75/Generative-Models-%EA%B8%B0%EB%B3%B8

NADE의 무궁무진한 가능성

1) Explicit Model
NADE는 Explicit model로, 단순히 무언가를 생성해낼 수 있을 뿐만 아니라, 새로운 입력이 주어졌을 때, 그 이미지가 얼마나 모델링하는 것에 likely한지 density를 구할 수 있다.

2) Continuous Variable
NADE는 discrete variable 뿐만 아니라 continuous variable에서도 사용할 수 있다. 대신, mixture of gaussian (MoG)가 같이 사용된다.

(참고)MoG가 뭔가요?
가우시안 혼합 모델은 여러 개의 가우시안 분포를 합쳐서 더 복잡한 분포를 만드는 방법이다. 주로 데이터가 단일 가우시안 분포로는 설명하기 어려운 복잡한 구조를 가질 때 MoG가 유용하다. (예: 이미지 색상 분포)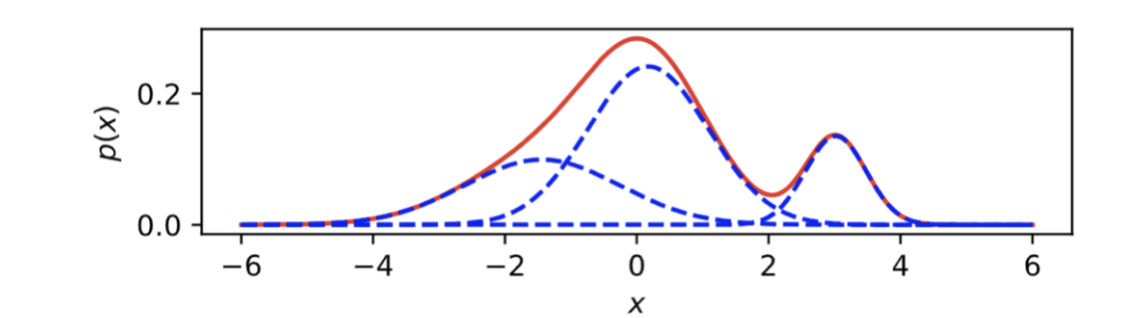

예시

Autoregressive Model 장점 총정리

1) Sampling이 쉽다.
Autoregressive Model(AR 모델)은 데이터를 순차적으로 샘플링할 수 있는 구조를 가지고 있습니다. 이에 시계열 데이터 분석과 고차원 데이터의 생성 모델링에서유리하다.

이는 다음과 같은 방식으로 작동한다.

전체 이미지 한번에 모델링하기 위해서는 큰 네트워크가 필요하다. 그런데 autoregressive model을 사용하면, 전체 input을 dimension별로 쪼개서 모델링하기 때문에 sampling이 쉽다. 예를 들어, 첫번째 order sampling을 하고 그 sampling 한 것을 고정한 상태에서 condition distribution에 따라 다음거를 sampling하고 등등 이렇게 sequential하게 sampling을 한다.

물론, 여기서의 단점도 존재한다. 데이터가 병렬로 처리되는 것이 아니다. 즉, i번째 값을 생성하기 위해서는 (i-1)번째 데이터가 필요하다. 따라서 생성이 느리다는 단점이 있다.