강아지 이미지를 생성하는 어떤 분포가 존재한다고 해보자. 우리는 그 분포를 모르지만 우리가 모델링할 수 있는 어떤 probability density를 어찌저찌 잘 조정해서 generative model과의 거리를 최소화하는 방향으로 해당 density를 최적화하고 싶을 것이다. 그러한 방식으로 최적의 강아지 이미지 생성 모델을 유추할 수 있을 것이기 때문이다.

Overview

강아지 이미지를 생성하는 어떤 분포가 존재한다고 가정해보자. 우리는 이 분포를 직접 알 수 없지만, 우리의 목표는 이 분포를 모델링하는 것입니다. 이를 위해, 모델링할 수 있는 확률 밀도 함수 (Probability Density, PDF)를 사용한다. 이 PDF를 조정하여 실제 강아지 이미지의 분포와 우리의 생성 모델 간의 거리를 최소화하는 방향으로 최적화할 것이다.

구체적으로는 다음과 같은 단계를 거친다:

1. 데이터 수집
다양한 강아지 이미지 데이터셋을 수집한다. 이 데이터는 우리가 목표로 하는 실제 분포에 근사한다.

2. 초기 모델 설정
강아지 이미지를 생성할 수 있는 초기 확률 모델을 설정한다. 예를 들어, Generative Adversarial Network (GAN)이나 Variational Autoencoder (VAE)를 사용할 수 있다.

3. 모델 학습
모델을 학습시키기 위해 실제 강아지 이미지 데이터셋과 생성된 이미지 간의 거리를 측정하는 손실 함수를 정의한다. 일반적으로 이 손실 함수는 두 분포 간의 차이를 측정하는 방법이다. (예: Kullback-Leibler Divergence, Wasserstein Distance 등)
위 손실함수를 통해 모델의 파라미터를 최적화하게 된다. 즉, 손실 함수를 최소화하는 방향으로 파라미터를 학습한다. 이를 통해 생성된 이미지 분포가 실제 강아지 이미지 분포에 가까워지도록 한다.

4. 모델 평가 및 조정
학습된 모델의 성능을 평가하고, 필요한 경우 모델을 조정하거나 개선한다. 이를 통해 생성된 이미지의 품질을 지속적으로 향상시킨다.

이 과정에서 우리는 실제 강아지 이미지의 분포를 직접 알 수 없지만, 생성 모델을 통해 이 분포를 근사할 수 있다. 최종적으로, 우리의 생성 모델은 고품질의 강아지 이미지를 생성할 수 있게 된다.

---

모델학습: Maximum likelihood learning

KL divergence를 손실함수로 활용하는 maximum likelihood learning은 Generative Model을 풀 수 있는 가장 쉬운 방법 중 하나로, 여기서부터 시작하겠다.

이 부분은 이전 포스팅인 최대가능도추정법과 쿨백-라이블러 발산에서 다루었다.

1) KL-divergence

간략하게 다시 설명하자면, Maximum Likelihood estimation이란, 특정 파라미터에 대해 주어진 데이터가 얼마나 likely한지에 관한 것이다. 우리는 이 likelihood를 높이는 방향으로 parameter를 학습하게 된다.
이 때 likelihood를 높이는 방향이란, 실제 데이터 분포와 모델 분포 간의 KL Divergence를 최소화하는 방향이다.

KL-divergence를 최소화하는 것은 모델 분포(expected log-likelihood)를 최대화하는 것과 같다. 그 자세한 과정과 이유는 아래와 같다.

(참고) empirical learning
원래는 $P(x)$는 모든 가능한 $x$에 대해 값을 구해야 한다. 예를들면, 모든 강아지 사진... 으로부터 구해야하는 것이다. 그런데 그건 불가능하지 않는가. 어떻게 모든 강아지 사진을 구하겠나! 따라서 우리는 수집된 데이터셋을 바탕으로 최대한 성능을 끌어내야 한다. 즉, D개의 dataset을 만들어 놓고 이 dataset에 대해서만 $Q(x)$가 높아지도록 maximum likelihood learning을 하겠다는 것이다. == Empirical Learning!

그러나 문제는 empirical learning을 할 경우, 데이터 수가 많지 않으면 정확한 결과가 나오지 않을 수도 있다는 문제가 있다. 즉, variance of Monte Carlo estimate이 높다는 문제가 있다.

2) Empirical Risk Minimization (ERM)

1. ERM 등장 배경: empirical learning
앞의 KL-divergence 식에서 원래 $P(x)$는 모든 가능한 $x$에 대해 값을 구해야 한다. 예를들면, 모든 강아지 사진... 으로부터 구해야하는 것이다. 그런데 그건 불가능하지 않는가. 어떻게 모든 강아지 사진을 구하겠나! 따라서 우리는 수집된 데이터셋을 바탕으로 최대한 성능을 끌어내야 한다. 즉, D개의 dataset을 만들어 놓고 이 dataset에 대해서만 $Q(x)$가 높아지도록 maximum likelihood learning을 하겠다는 것이다. == Empirical Learning!

그러나 문제는 empirical learning을 할 경우, 데이터 수가 많지 않으면 정확한 결과가 나오지 않을 수도 있다는 문제가 있다. 즉, variance of Monte Carlo estimate이 높다는 문제가 있다.

2. ERM 목표
ERM은 전체 데이터 분포를 알 수 없는 상황에서 주어진 샘플 데이터로 리스크를 최소화하는 접근법이라고 할 수 있다. 즉, 모델이 훈련 데이터에 대해서만 overfitting되는 것이 아니라, 전체 데이터 분포에 대해 generalization이 잘 되도록 하는 것이 목표이다. 이러한 ERM은 maximum likelihood learning와 함께 종종 사용된다.

3. ERM 수식
앞에 거창한 목표치고 ERM은 매우 간단하다. 그저 손실함수들의 평균값을 최소화하는 방법이다.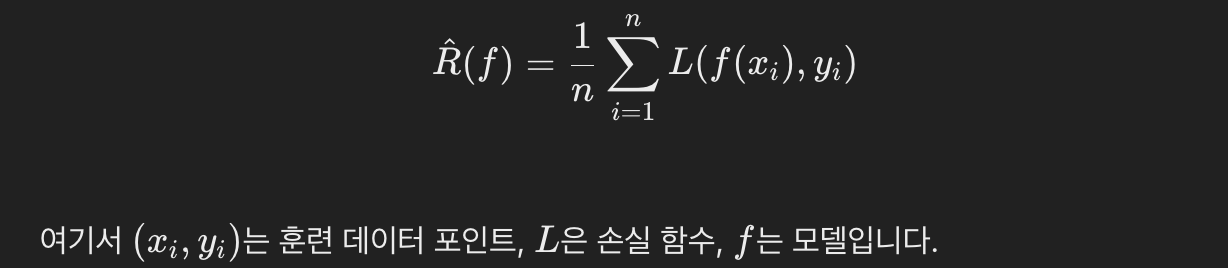

3) Similarity 측정을 위한 다른 방법론

1. MLE 한계점
앞서 KL-divergence를 활용한 Maximum likelihood learning에 대해 살펴보았다.
이 과정에서 우리는 현실적인 이유로 hypothesis space를 줄여야 한다. 왜냐하면, 모든 가능한 확률분포 공간을 사용하면 파라미터가 너무너무 많을 것이며, 적당히 hypothesis space를 줄여 파라미터 수를 줄이면 generalization performance가 높아지기 때문이다.

이 때 우리는 최적화를 위해 gradient descent를 사용한다. 그러려면 미분가능한 log likelihood를 사용해야하고, 미분 가능한 만만한 함수가 가우시안이기 때문에 가우시안을 종종 사용한다. 가우시안으로 maximum likelihood estimation을 한다는 것이 무슨 말인가?

likelihood값이 최대가 될 수 있는 평균과 표준편차 (가우시안 분포의 파라미터)를 구해야한다는 것이다. 즉, 평균과 분산을 변수로 가지는 가우시안 분포에서 각각 평균과 분산으로 편미분하였을 때 0이 되는 지점을 찾아야 한다는 것이다. (https://xoft.tistory.com/31 << 이 링크를 통해 더 자세한 내용을 살펴보자)

그러나 가우시안으로는 유의미한 분포를 모델링하기 어렵다는 문제가 있다. 따라서 Maximum likelihood 외에도 similarity 측정을 위한 다양한 방법론이 제시되었다.

2. 다양한 방법론

---

Latent Variable Models

잠재 변수 모델(Latent Variable Models)이란 관찰 가능한 데이터에서 직접 측정할 수 없는 '잠재 변수'를 이용해 모델을 구성하는 방식이다. 잠재 변수는 직접 관찰되지 않지만 관찰 가능한 데이터의 분포를 설명하는 데 중요한 역할을 하는 변수이다. 예를 들어, 사용자의 구매 패턴에서 각각의 구매 이벤트는 관찰 가능하지만, 사용자의 숨겨진 구매 선호도는 직접적으로 관찰할 수 없는 잠재 변수가 될 수 있다.
[출처] https://wikidocs.net/200922

즉, 잠재변수모델은 복잡한 데이터를 더 잘 모델링하고 새로운 데이터 생성에 중요한 역할을 하므로 Generative model파트에서 배워보도록 하겠다.

1) Autoencoder

autoencoder는 입력이들어오면 encoder를 거쳐서 latent vector를 만들고, 나아가 decoder를 거쳐 원래 입력으로 복원하는 과정을 말한다. 참고로, 얘 자체는 generative model이 아니라 그냥 어떤 모델이다. 입력으로 feature를 뽑고, 다시 output을 만들어내는 그냥 어떤 모델이다. autoencoder에 대해 아래에서 조금 더 자세히 설명해보도록 하겠다. 참고로 아래 내용은 https://zrr.kr/Qh1K 를 정리한 것이다.

1. Autoencoder 의미
autoencoder는 세상에 존재하는 사물의 특징을 스스로, 어떠한 데이터 라벨도 없이 학습한다는 것이다.
나아가 앞서 설명하였듯이, autoencoder는 이름만 보면 encoding에 초점이 맞춰있는 듯 하지만, decoding도 가능하다. 즉, 'generation'도 가능하다는 의미이다.

2. Autoencoder 구조
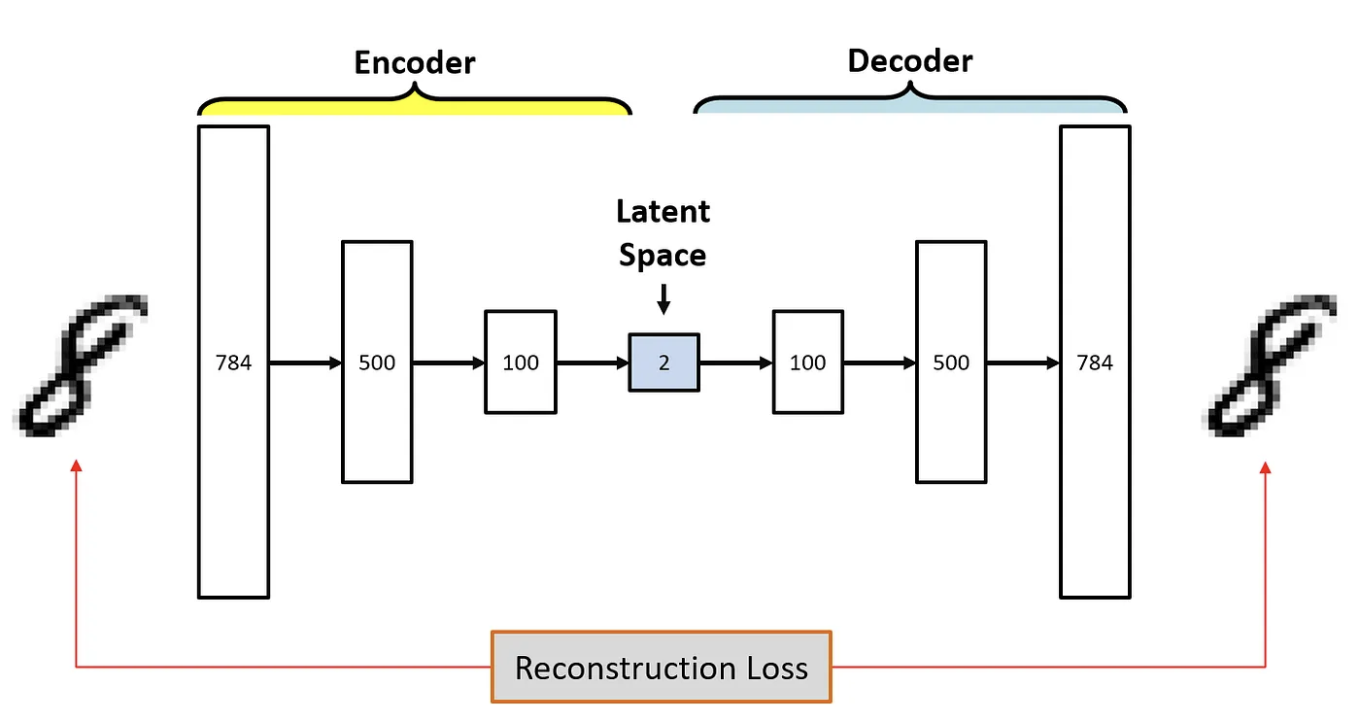
Autoencoder의 목표는 input 데이터(x)가 주어졌을 때, 최종적으로 output 데이터가 input 데이터와 동일한 값(x)을 출력하도록 하는 것이다.

구체적으로, 오토인코더는 입력 데이터를 인코딩(encoding)하여 저차원 잠재 공간(latent space) 표현으로 압축한 후, 다시 디코딩(decoding)하여 원래 입력 데이터를 재구성(reconstruction)하는 신경망 구조이다. 여기서 latent space는 bottleneck이라고 한다. 참고로 bottleneck의 차원이 높을수록 더 세밀한 정보까지 데이터를 latent space에서도 표현할 수 있을 것이다. (물론 bottleneck의 목적이 차원을 줄이는 것이라 한없이 키우면 당연히 안되지만 말이다.) (참고로 bottleneck이라는 단어 어딘가 익숙하지 않은가? image segmentation에서도 유사한 과정이 있다. output형태는 조금 다르지만 말이다.)

학습 과정에서 주로 사용하는 데이터는 레이블이 없는 원래 데이터 그 자체이다. 이 과정에서 사용하는 손실 함수(loss function)는 주로 재구성 오차(reconstruction error)로, 원래 입력 데이터와 재구성된 데이터 간의 차이를 측정하는 함수이다.

이 과정을 살펴보면 어디에도 사람의 노력이 들가지 않는다. 그냥 레이블 없는 데이터를 모델에 넣어주면 알아서 학습하는 것이다. 즉, autoencoder는 unsupervised learning이다.

이미지 출처 https://zrr.kr/Qh1K

3. Autoencoder 한계점
Autoencoder는 이쪽 업계(?)에서 가장 단순한 구조로, 이걸 그대로 사용하기에는 부족함이 있다. 구체적인 예시는 다음과 같다.

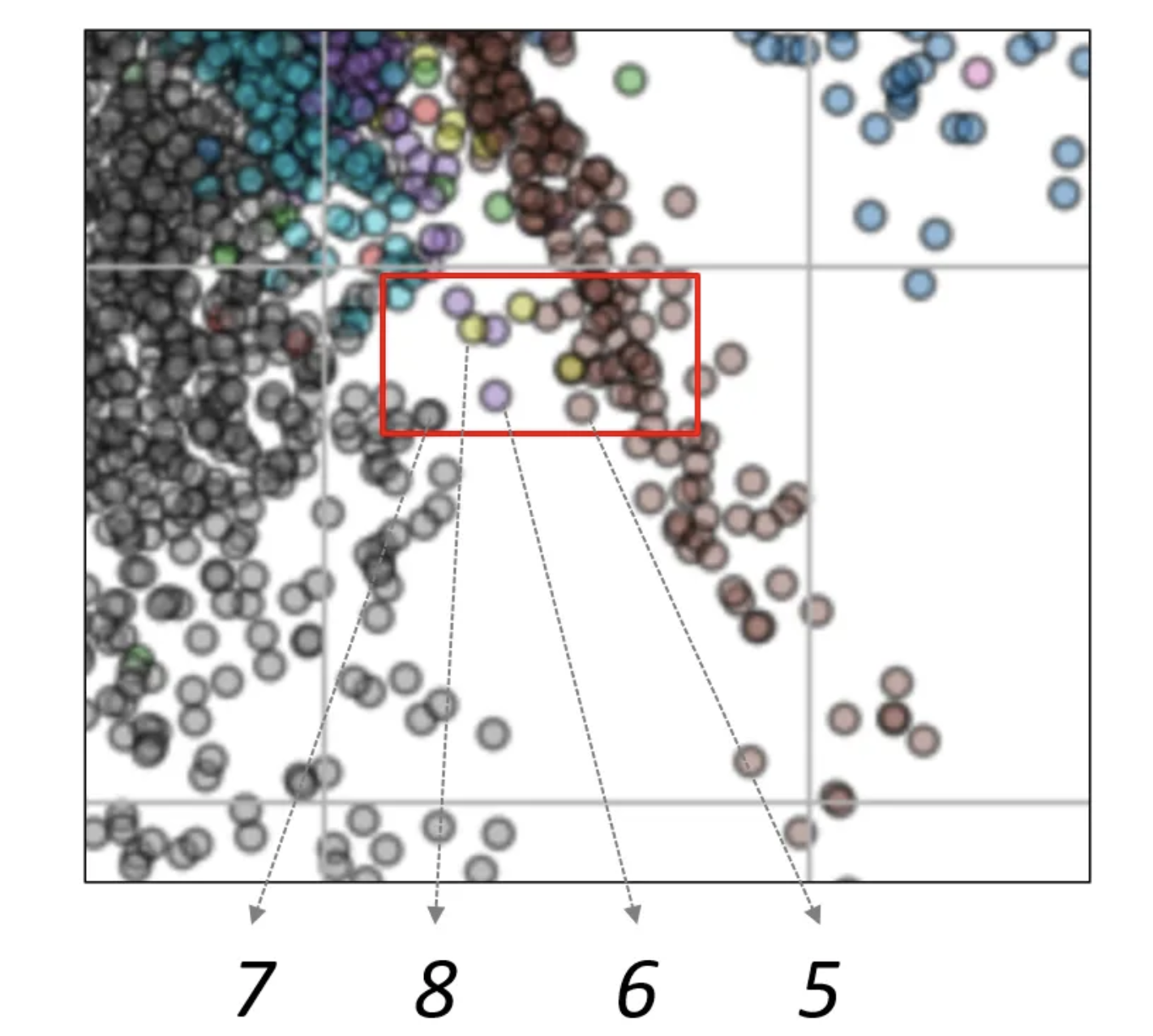
• 학습을 통해 도출된 잠재공간의 해석이 어렵다.
• 학습된 잠재공간이 연속적이지 않다.
• 생성된 데이터가 원본데이터보다 품질이 떨어진다.
  

2) Variational Autoencoder (VAE)

1. Autoencoder vs Variational Autoencoder

• Autoencoder: 오토인코더는 잠재공간에 대한 제약 없이 학습이 되기 때문에, 잠재공간이 벡터의 형태로 고정된다.
• Variational Autoencoder: VAE는 잠재공간을 영역/분포로 표현한다. 이 영역을 우리가 가장 잘 아는 연속공간인 가우시안 분포로 표현하게 된다. 즉, 가우시안 분포를 통해 잠재공간을 구성함으로써 데이터 포인트들이 연속확률분포로 나타나게 한다.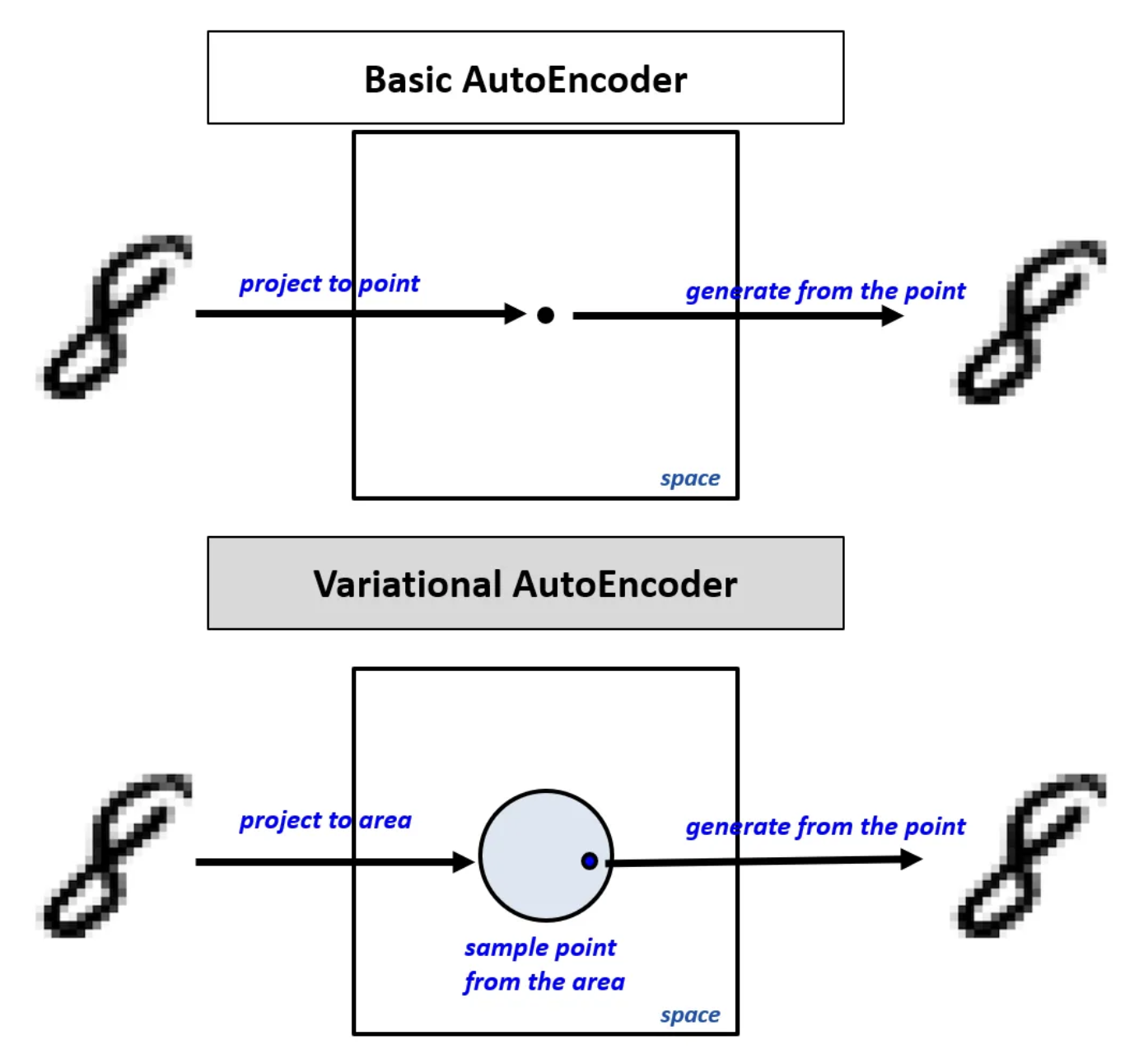 이미지 출처: https://zrr.kr/Qh1K

2. 가우시안 분포를 통한 잠재공간 구성

가우시안 분포로 잠재공간을 구성하기 위해서는 평균(μ)과 표준편차(σ) 파라미터가 필요하다. 평균과 표준편차 각각 1개씩만 있으면 우리가 아는 1차원 상에서의 가우시안 분포가 나오고, 각각 2개 총 4개의 파라미터로는 2차원 공간 상에서의 가우시안 분포를 결정할 수 있게 되며, 만약 8개의 파라미터가 주어진다면 2차원 공간 상에서 2개의 가우시안 분포로 다음과 같은 모양을 형성하게 된다. 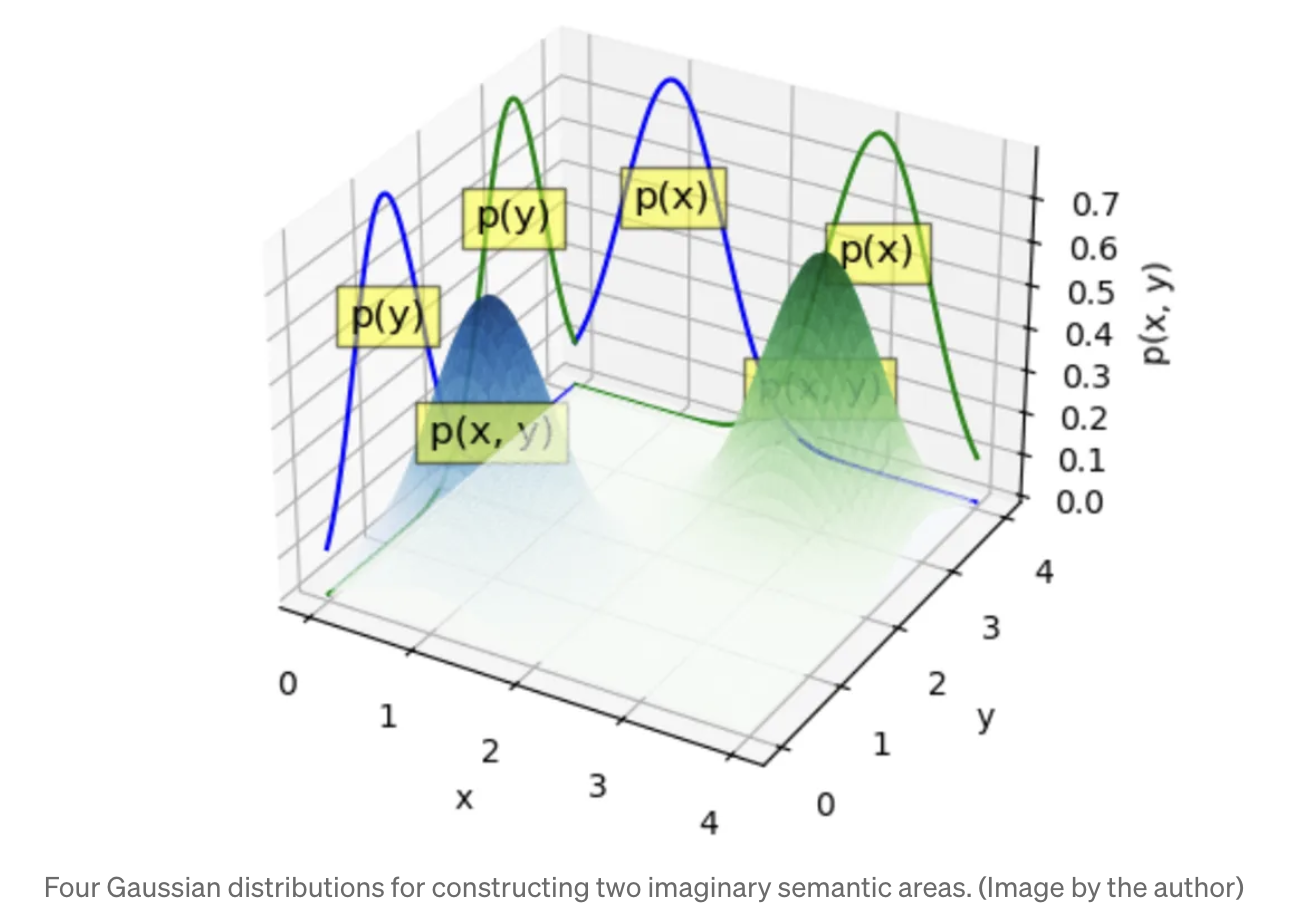이미지 출처: https://zrr.kr/Qh1K

즉, M개의 정규분포를 통해 다양한 차원의 잠재공간에서 다양한 모양의 확률분포를 모델링할 수 있는 것이다. 가우시안 분포를 통해 latent space를 모델링한다는 것을 도식화하면 다음과 같다. 아래 이미지에서 알 수 있는 바와 같이, 원래 autoencoder라면 초록 박스, sampled latent vector만 존재했을텐데, VAE에서는 그 앞 layer에 평균과 표준편차에 대한 벡터가 추가되었다. 즉, VAE는 오토인코더 학습 시, latent vector를 학습하는 것이 아니라, 가우시안 분포 파라미터인 𝜇(mean)와 𝜎(variance)를 학습한다.

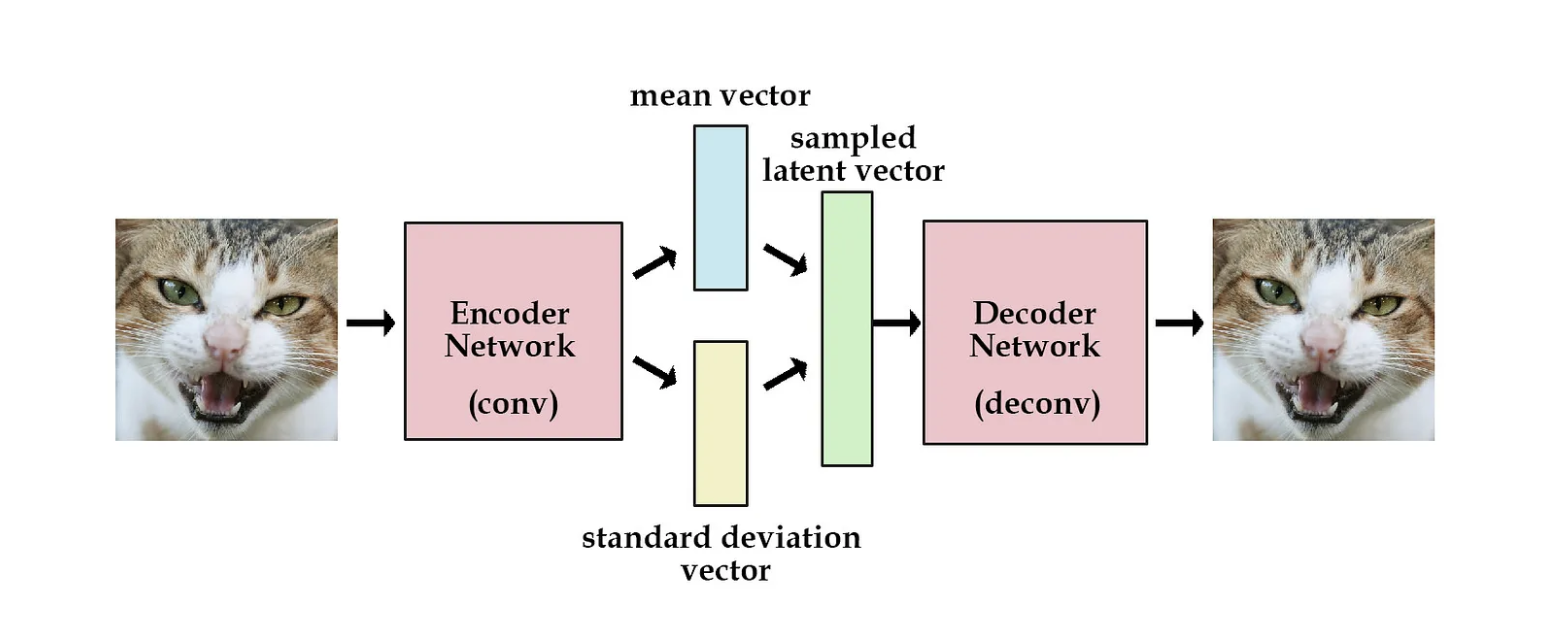
자, 그런데 디코더 입장에서는 확률분포가 아니라 하나의 의미있는 값을 지니고 있는 벡터가 필요하다. 따라서 우리는 encoding 과정에서 구한 확률분포에서 적절한 벡터를 샘플링하게 된다. 아래 이미지에서 파란색의 확률분포에서 빨간색 점을 sampling하는 것이다.
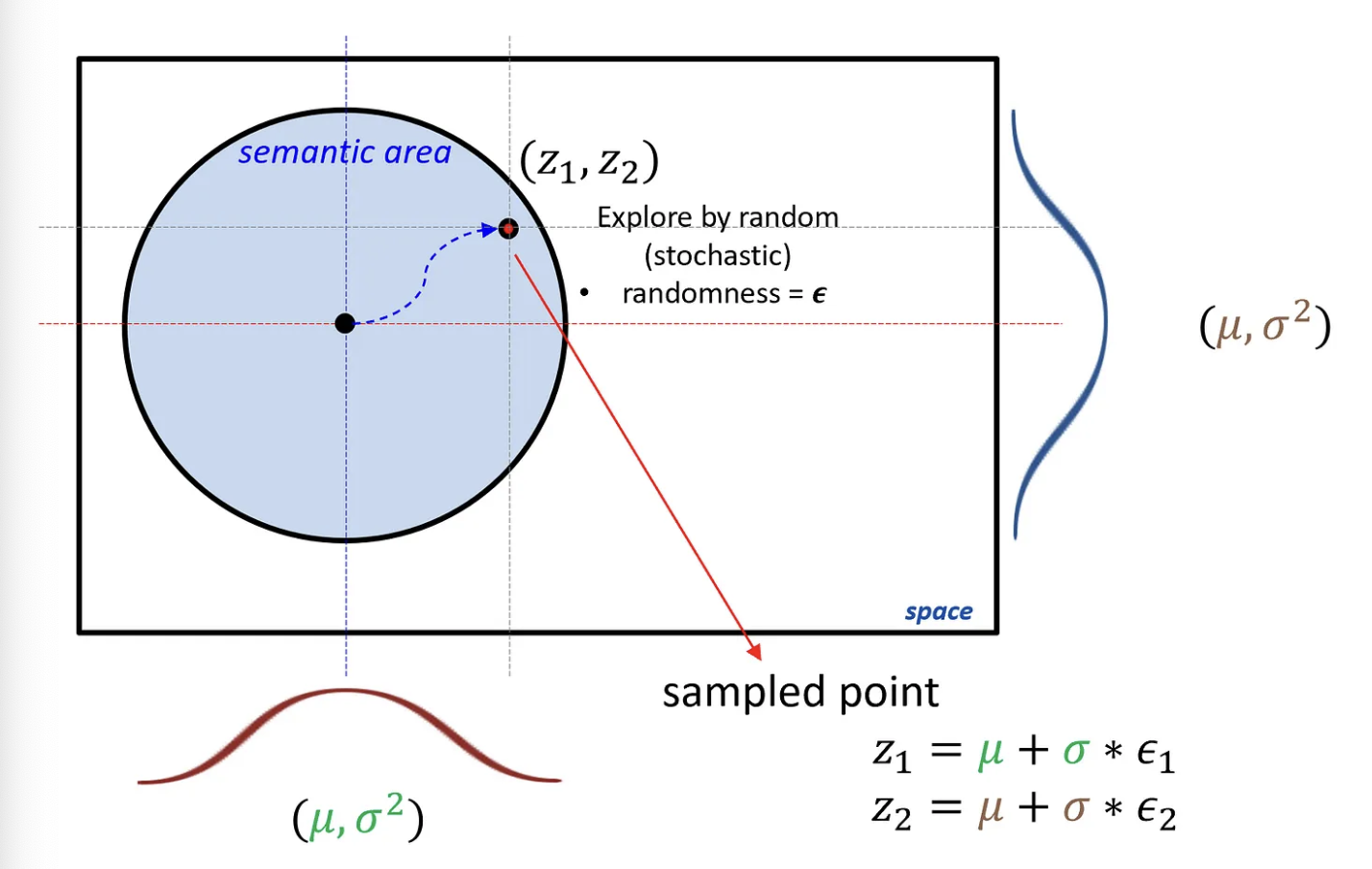이미지 출처: https://zrr.kr/Qh1K

그런데 문제가 있다. 우리는 모델 학습에 있어 backpropagation 과정을 통해 모델을 지속적으로 업데이트 해주어야 하는데, 샘플링 과정은 무작위성이 포함되어있기 때문에 인코더부분까지 backpropagation이 잘 이루어지지 않는다는 것이다.

이를 해결하기 위해 Reparameterization Trick(재파라미터화 트릭)이 제시되었다.

3. Reparameterization Trick (재파라미터화 트릭)

재파라미터화 트릭은 역전파가 가능하도록 샘플링 과정을 변환하는 기술이다.
구체적으로, 재파라미터화 트릭에서 잠재 변수 𝑧는 다음과 같이 표현된다:
z=μ+σ⋅ϵ
여기서 ϵ∼N(0,1)는 표준 정규 분포에서 샘플링되는 무작위 변수이다.
이를 통해 샘플링 변수의 통계적 성질은 유지하면서 역전파도 가능하게 된다.

왜 그런지 자세히 설명해보겠다.

1) 샘플링 변수의 통계적 성질 유지

• 표준정규분포의 특성
  • ϵ은 표준정규분포 N(0,1)를 따르며, 이는 평균이 0이고 표준편차가 1이다.
• 선형 변환
  • 표준정규분포에서 샘플링한 값 ϵ에 σ를 곱하면, 표준편차가 σ인 분포가 된다.
  • 즉, σ⋅ϵ는 평균이 0이고 표준편차가 σ인 분포를 만든다.
• 평균 이동
  • σ⋅ϵ에 μ를 더하면 평균이 μ로 이동한다.
  • 따라서, μ+σ⋅ϵ는 평균이 μ이고 표준편차가 σ인 분포를 만든다.

2) 역전파 과정에서의 편미분

• μ에 대한 편미분
  • $\frac{\partial z}{\partial \mu} = 1$
    이 경우, 𝜇는 단순히 더해지는 항이므로, 그 편미분 값은 1이다.
• σ에 대한 편미분
  • $\frac{\partial z}{\partial \sigma} = \epsilon$
    σ가 ϵ에 곱해지는 형태이기 때문에 σ에 대한 편미분은 ϵ이다.
    (질문) ϵ는 매 미니배치마다 새로 샘플링되기 때문에 매번 다른 값이 나오는거 아닌가요?
    맞다. 평균에 대한 편미분은 계속 1로 유지되겠지만 시그마에 대해서는 매 미니배치마다 입실론이 바뀌니 값이 조금씩 바뀐다. 그래도 Monte Carlo 샘플링을 통해 평균적으로 안정적인 그래디언트를 제공한다. 즉, 샘플 수가 증가할수록 평균이 0에 수렴하게 되므로 평균적으로 안정적인 업데이트가 가능하다.

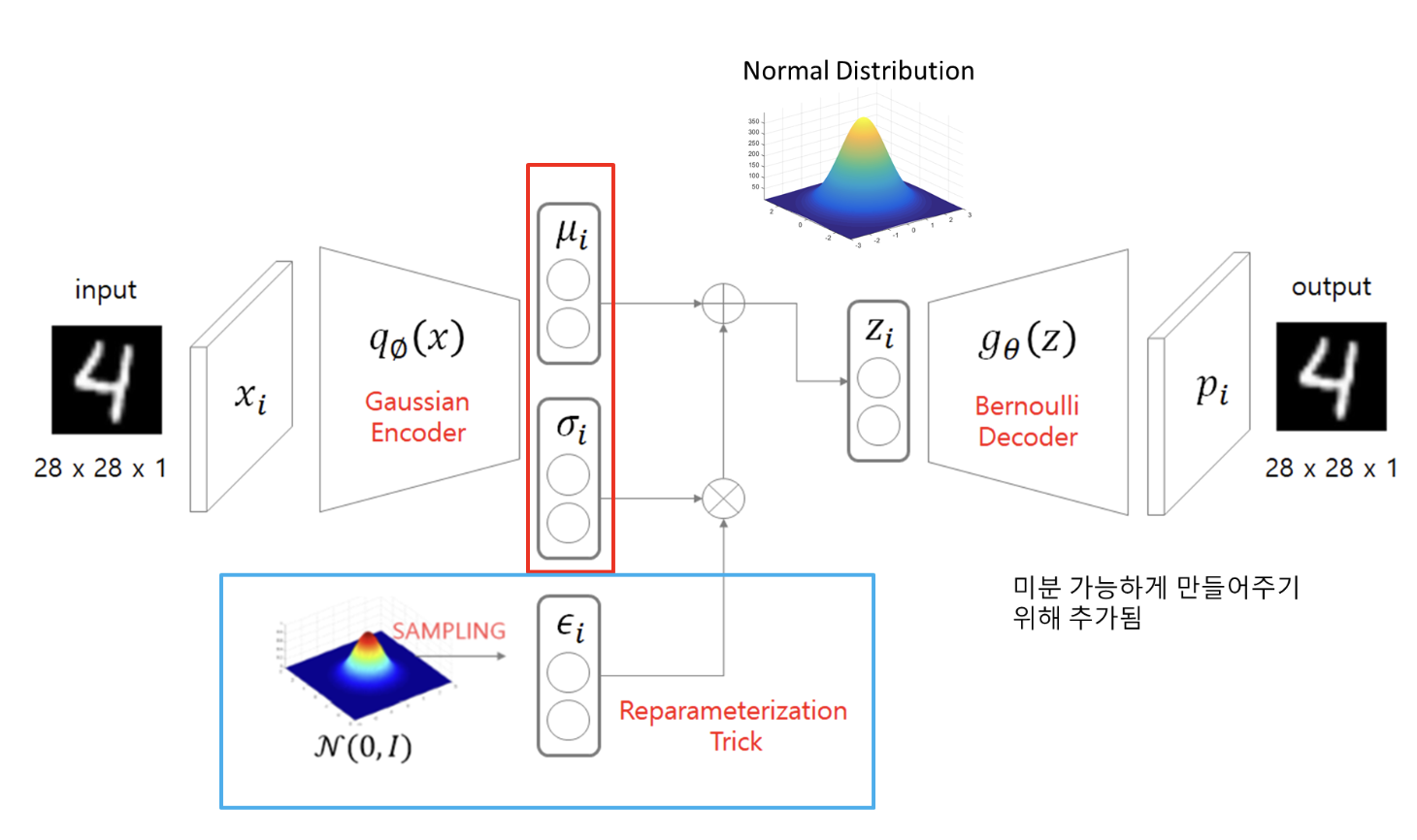이미지 출처: https://velog.io/@gunny1254/Variational-Auto-Encoder-VAE

4. VAE의 손실함수

과거에는 모델 파라미터 $\theta$에 대해 단순하고 표현력이 낮은 사전분포 $p(\theta)$를 사용하여 모델을 학습하였다. 그러나 이러한 접근은 underfitting 문제를 초래할 수 있다. 이에 ML/Inference에 많이 활용되는 Variational Inference(VI)에 대해 배워보고자 한다. 그리고 이는 VAE의 손실함수이기도 하다.

• 목적
  • VI의 목적은 Posterior Distribution (후방분포)와 최대한 유사한 Variational Distribution (변분분포)를 찾는 것이 목표이다. 이 때 KL-divergence를 최소화하는 방식으로 두 분포 간의 차이를 줄인다.
  • Posterior Distribution이란, 베이지안 추론에서 주어진 데이터 𝑥에 대해 잠재변수 𝑧의 분포를 나타낸다. 즉, 데이터가 관찰된 후, 잠재변수의 조건부 분포를 의미하며, 베이지안 정리에 따라 다음과 같이 정의된다. $p(z|x) = \frac{p(x|z)p(z)}{p(x)}$ 문제는 이 분포를 정확하게 계산하기는 매우 어렵다는 것이다. 특히 고차원에서의 적분 계산을 필요로하기 때문에 실질적으로 불가능한 경우가 많다.
  • Variational Distribution이란, 후방분포 $p(z|x)$를 정확하게 계산하기 어려우므로 이를 근사하는 $q(z|x)$라는 분포를 사용하는 것이다.

• 변분추론 Variational Inference
  VAE의 목표는 관찰된 데이터 x의 가능도 p(x)를 최대화하는 것이다. 즉, 최대우도가능도 $\log p(x)$를 최대화하는 것이다. 그런데 앞서 이야기하였듯이, p(x)를 계산하기는 매우 어렵다. 변분추론은 이러한 어려움을 해결하기 위한 방법으로, q(z|x)를 어찌저찌 잘 지지고 볶게 된다. 그러면 다음과 같은 식이 나오게 되며, ELBO라는 개념이 나오게 된다.
  좀 더 설명하자면, $\log p(x)$ = ELBO(Evidence Lower Bound) + Variational Gap 이다. 이 때, Variational Gap은 우리가 계산으로, 수식으로 풀어낼 수 없는 부분이다. 따라서 Maximum Likelihood Learning인 $\log p(x)$를 최대화하려면 ELBO를 최대화해야 한다.
  

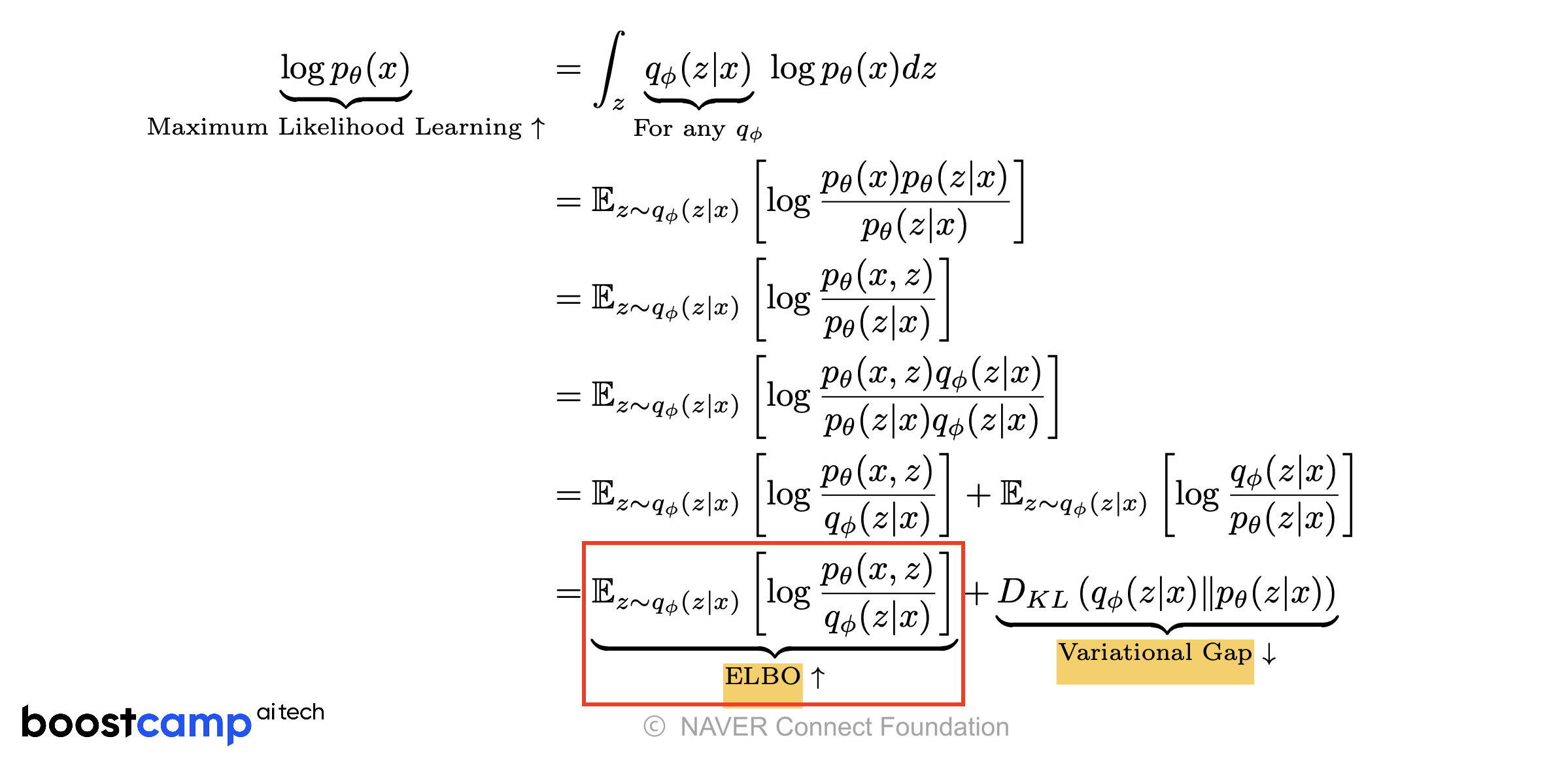
  EBLO에 대해 더 살펴보자. ELBO를 더 뜯어보면,
  EBLO = Reconstruction Term + Prior Fitting Term 이라는 수식이 나온다. 그럼 각각이 무엇을 의미하는 것인지 살펴보자.

  • Reconstruction Term

  • Latent Space Regularization Loss
    

    

5. VAE의 한계점

• Intractable Model
  VAE는 데이터의 가능도를 직접 계산하기 어려운 모델이다. 이에 근사를 통해 최적화를 수행하고 있으므로 encoder, decoder를 정확한 확률분포로 보기 어렵다.

• Prior Fitting Term (=Latent Space Regularization Loss)
  사전 분포는 미분 가능해야 하기 때문에 주로 가우시안 분포만 사용하게 된다는 한계가 있다.
  (참고) 이러한 한계를 극복하기 위해 AVB, AAE 등의 모델이 제안되기는 하였다.