이번시간에는 다음 내용을 배운다.
1. 기계학습에서 데이터가 새로 추가될 때마다 정보를 업데이트하는 방법론인 베이즈 정리
2. 인과관계 추론 방법
베이즈 정리
- 조건부 확률
: 사건 B가 일어난 상황에서 사건 A가 발생할 확률
위 간단한 식을 잘 지지고 볶으면 다음과 같은 베이즈 정리가 탄생한다.
혹시나 궁금할 사람을 위해 그 과정을 첨부해두겠다. 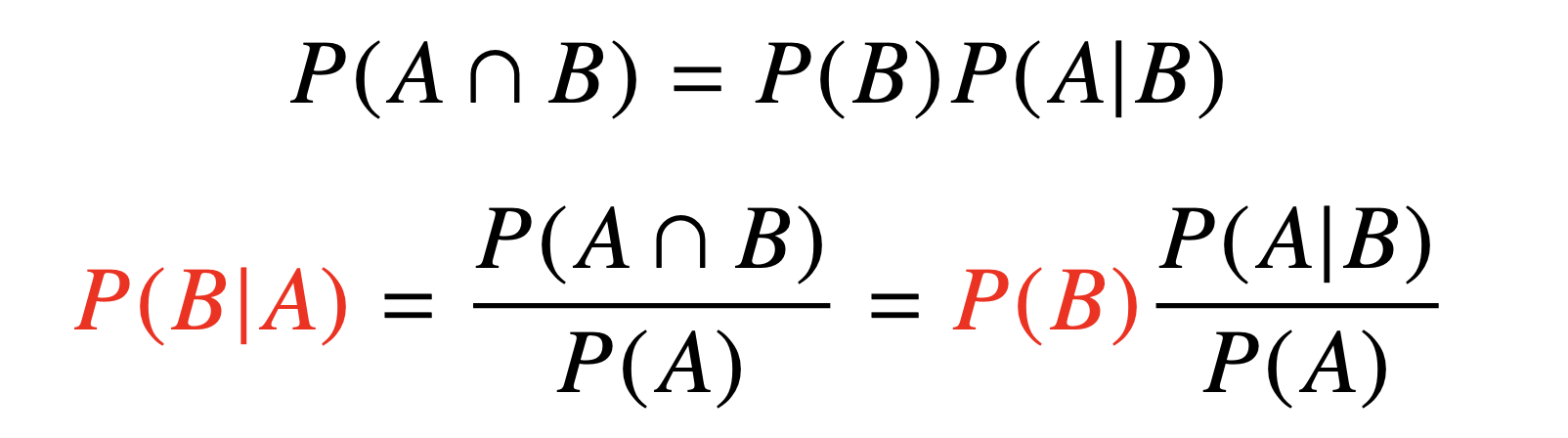
베이즈 정리 정의

각 용어의 정의


예제

1. 문제를 수식으로 표현하기
-
실제로 걸린 경우: A
검진될 확률: D -
묻는 질문: P(A|D)
사용가능한 수식: -
문제의 수식화
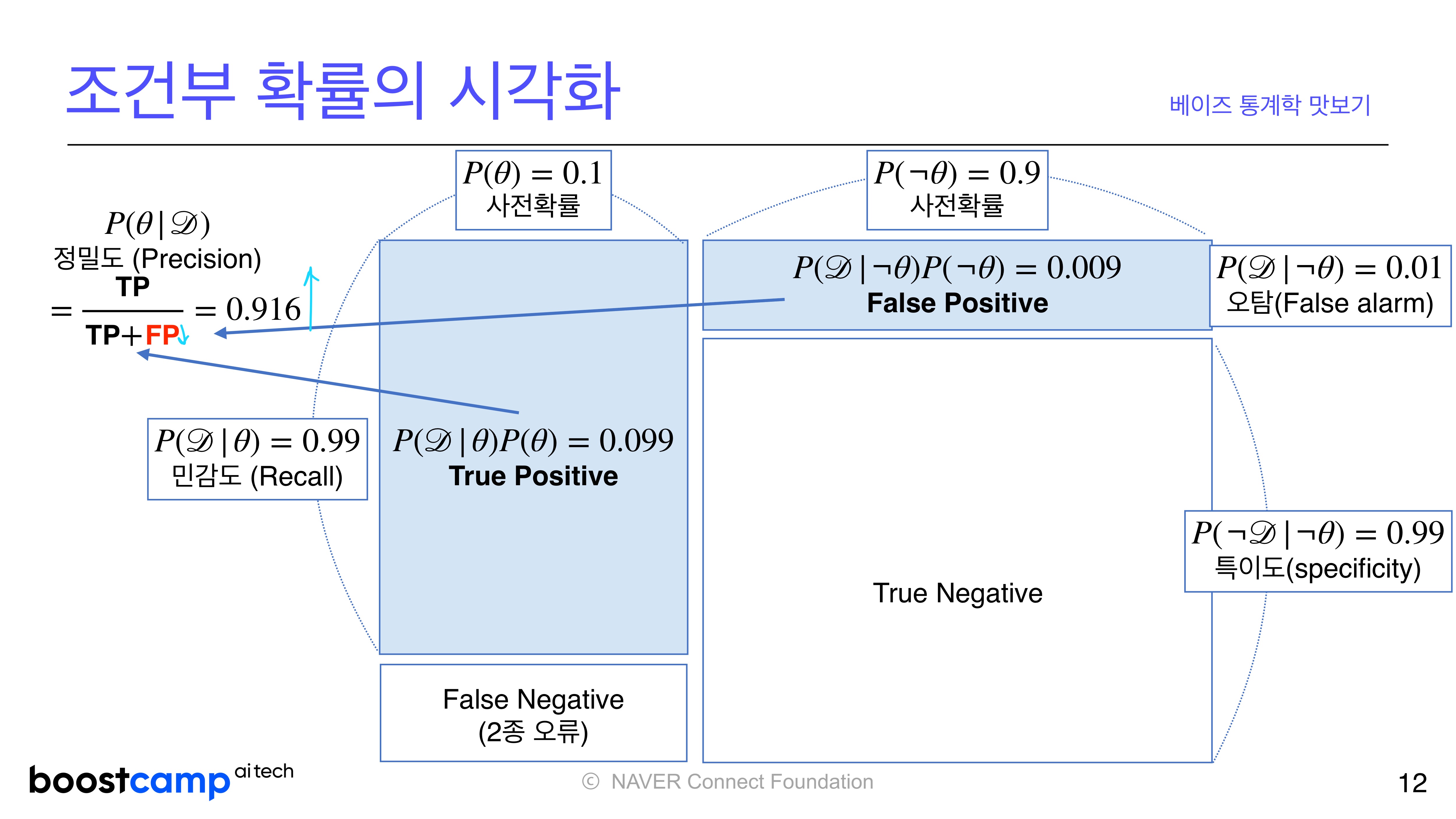
P(D|A) = 0.99
P(D|~A) = 0.01
P(A) = 0.1
2. 문제 풀기
= 0.99 0.1 + 0.01 0.9 = 0.108
= 0.1 * 0.99 / 0.108 = 0.916
3. 정답 : 0.916
베이즈 정리의 Problem
오탐율(False Positive Rate)가 오르면 테스트의 정밀도(Precision)가 매우 떨어진다.

베이즈 정리를 통한 정보의 갱신
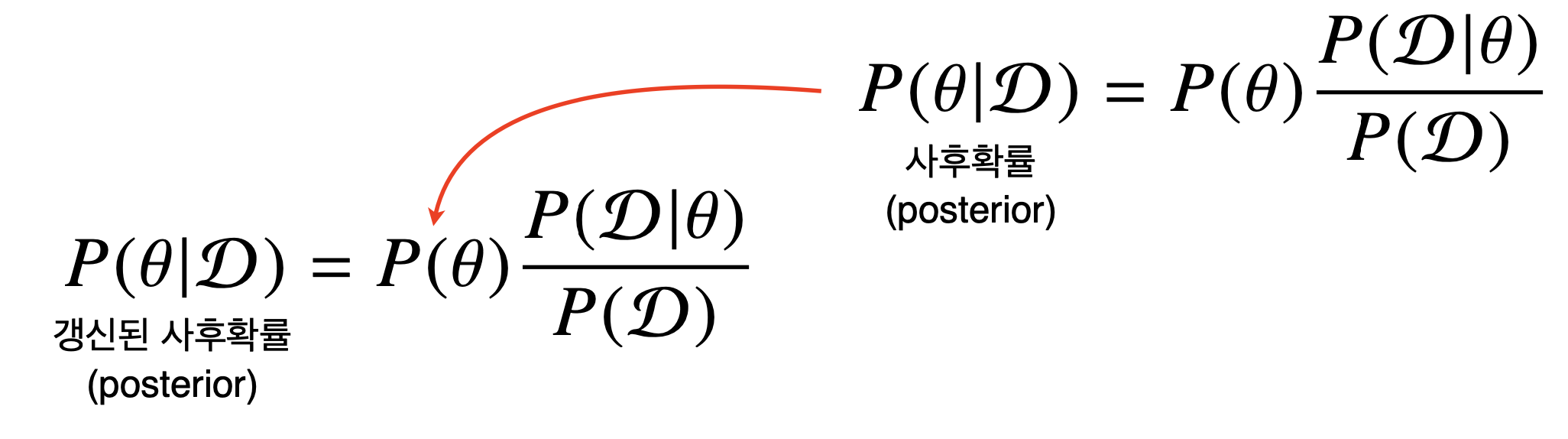
새로운 데이터가 들어왔을 때 베이즈 정리를 통해 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산할 수 있다.
즉, 베이즈 정리를 통해 데이터를 새로 관찰할 때마다 hypothesis나 parameter를 점점 update하는 것이 가능해진다.
정보 갱신 예시
여기서의 핵심은 이전의 사후확률이 이후의 사전확률로 사용된다는 것이다.





인과관계 추론
조건부확률은 인과관계(causality)를 추론할 때 사용하면 안된다.
인과관계를 예측 모델에서 고려해야 하는 이유
이는 데이터 분포의 변화, 새로운 시나리오에서도 강건한 모델을 만들기 위해 필요하다. 만약 조건부확률만을 고려하고 인과관계를 고려하지 않으면, 실제 테스트 시에는 높은 정확도를 보이나, 데이터 분포가 바뀌는 경우 (e.g., 새로운 정책이나 치료법이 도입되었을 때) 예측 확률이 크게 떨어질 수 있다. 따라서 데이터 변화에 강건한 모델을 만들고 싶다면 인과관계를 기반으로 예측모형을 만들어야 한다. 그렇지 않으면, 시나리오마다 예측정확도가 매우 달라질 수 있다. 단, 인과관계만 고려하면 높은 예측 정확도를 담보하기 어려울 수 있다. 
중첩요인(confounding factor)
인과관계를 알아내기 위해서는 중첩요인의 효과를 제거하고 원인에 해당하는 변수만의 인과관계를 계산해야 한다. 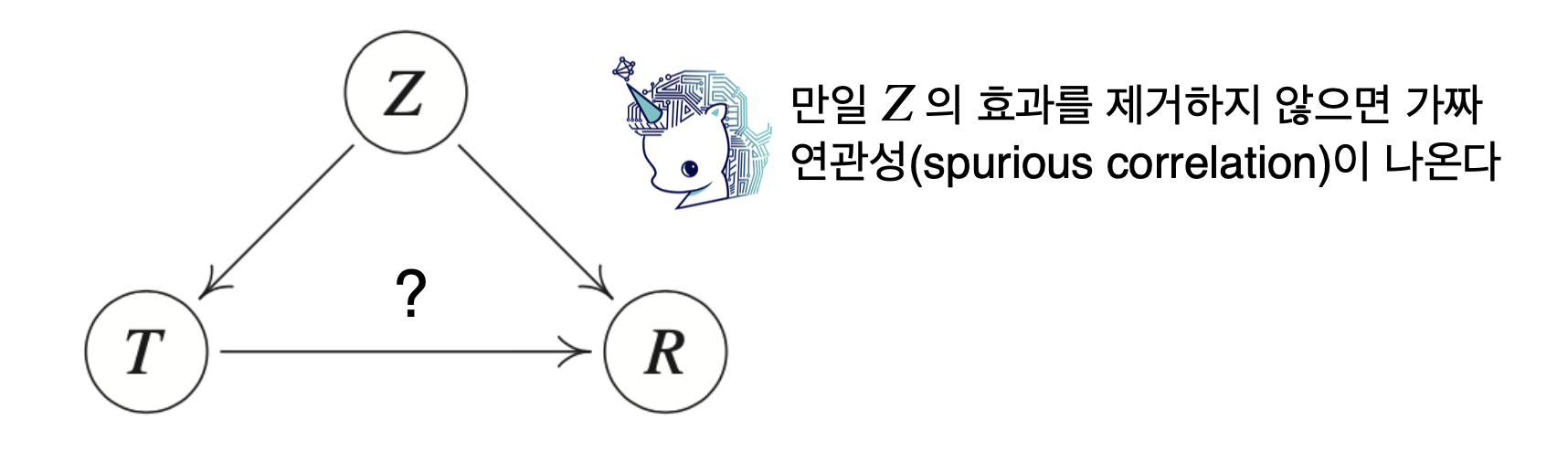
T: 키, R: 지능지수, Z: 나이 라고 했을 때, 키가 크면 지능지수가 높다라는 결과만 보면 키가 지능지수에 영향을 미치는 원인이라고 생각할 수 있으나, 사실은 나이라는 중첩요인을 제거해야한다. 나이가 많으면 키가 커지고 지능지수도 높아지니까요!
예제
Simpson’s Paradox
이 블로그에 정리가 정말 잘 되어있다!
https://medium.com/bondata/simpsons-paradox-and-confounding-190a26f9e039
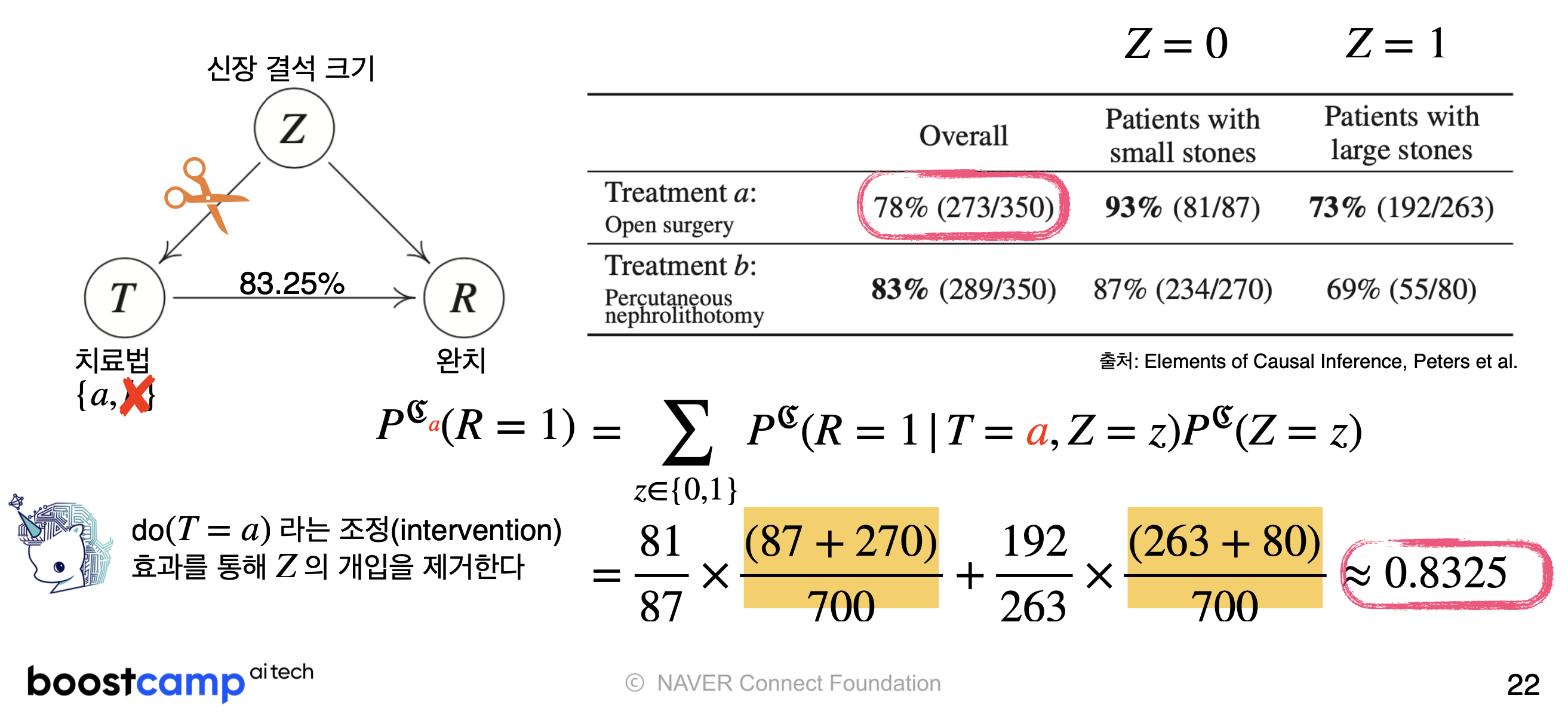
Q. 새로운 질병에 대한 치료법 a와 치료법 b 중 어떤 방법이 더 효과적인가?
전체 확률로만 보면 치료법 b는 83%, 치료법 a는 78%로 치료법 b가 더 좋아보인다. 그런데 환자의 중증도에 따라 계층화하여 살펴본 결과에 따르면 mild한 상태였던 환자, 중증환자 모두 치료법 a가 더욱 효과적이라는 모순적인 결과가 확인된다. 이러한 현상을 simpson's paradox라고 부른다.
A, B 그룹의 유저 수 구성을 자세히 살펴본다면 Simpson’s Paradox 현상의 원인을 알 수 있다. Treatment a는 중증환자의 수가 훨씬 많으며, treatment b는 mild한 상태의 환자가 훨씬 많다. 즉, 각 Treatment 그룹을 구성하는 Condition의 가중치 때문에 그룹 전체를 평균 내었을 때 숫자에 왜곡이 발생한 것이다.
해결책