[DL 수학] - 2) 확률론 맛보기

cherry·2024년 6월 19일

목록 보기

4/21

아래 내용은 네이버 AI precourse 강의를 개인 공부를 위해 정리한 내용입니다.

딥러닝에서 확률론이 필요한 이유: 분산 및 불확실성을 최소화하기 위해
1. 회귀 분석: 손실 함수로 사용되는 L2 Norm에서 예측오차의 분산을 최소화하는 방향으로 학습하기 위해
2. 분류 문제: 교차엔트로피(cross-entropy)에서 모델 예측의 불확실성을 최소화하는 방향으로 학습하기 위해

데이터 공간과 분포

1) 데이터 공간 (Data Space)

𝒳: 입력 데이터의 공간
- 모델이 학습할 입력 데이터의 모든 가능한 값을 포함한다.
- 예를 들어, MNIST Dataset에서 모든 가능한 손글씨 숫자 이미지 (28x28 픽셀 값) 의 집합을 의미한다.
𝒴: 출력 데이터의 공간
- 모델이 예측하려는 출력 값의 모든 가능한 값을 포함한다.
- 예를 들어, MNIST Dataset에서 각 이미지에 대한 가능한 레이블의 집합을 의미한다.
𝒳×𝒴: 입력 데이터 공간과 출력 데이터 공간의 곱집합(cartesian product)
- 가능한 모든 (입력, 출력) 쌍의 집합을 의미한다.
- 예를 들어, MNIST Dataset에서 (이미지, 레이블) 쌍의 집합을 의미한다.

2) 데이터 분포 (Data Distribution)

𝒟: 데이터 공간에서 데이터를 추출하는 확률 분포
- (입력, 출력) 쌍이 어떻게 분포되어 있는지를 나타내는 확률 분포
- 예를 들어, 𝒟는 어떤 이미지가 어떤 레이블을 가질 확률을 나타낸다.
  손글씨 이미지 데이터 세트가 있다고 가정해 보자. 이 데이터 세트에서 각 손글씨 이미지가 어떤 숫자(레이블)를 나타내는지를 확률적으로 설명하는 분포가 𝒟이다. 구체적으로, 특정 손글씨 이미지가 '3'이라는 레이블을 가질 확률을 𝒟가 결정합니다.
데이터 분포가 중요한 이유
- 학습 데이터의 생성: 모델이 학습할 데이터는 이 분포 𝒟로부터 샘플링된다.
  이는 학습 데이터가 실제 세계의 데이터를 얼마나 잘 반영하는지를 결정한다.
  예를 들어, 손글씨 인식 모델을 학습시킬 때, 학습 데이터가 실제 손글씨의 다양한 변형을 잘 반영하고 있어야 모델이 잘 학습될 수 있습니다.
- 일반화: 모델이 새로운 데이터를 얼마나 잘 예측할 수 있는지는 이 분포𝒟를 얼마나 잘 학습했는지에 달려 있다. 학습 데이터가 분포 𝒟를 잘 반영하고 있다면, 모델은 새로운 데이터에 대해 더 잘 일반화할 수 있다.

확률변수의 종류

1) 이산 확률변수 (Discrete Random Variable)

값이 이산적(독립적이고 구분 가능한)인 경우
- 예: 주사위 던지기의 결과 (1, 2, 3, 4, 5, 6), 동전 던지기의 결과 (앞면, 뒷면)
확률질량함수(PMF, Probability Mass Function)가 사용됨
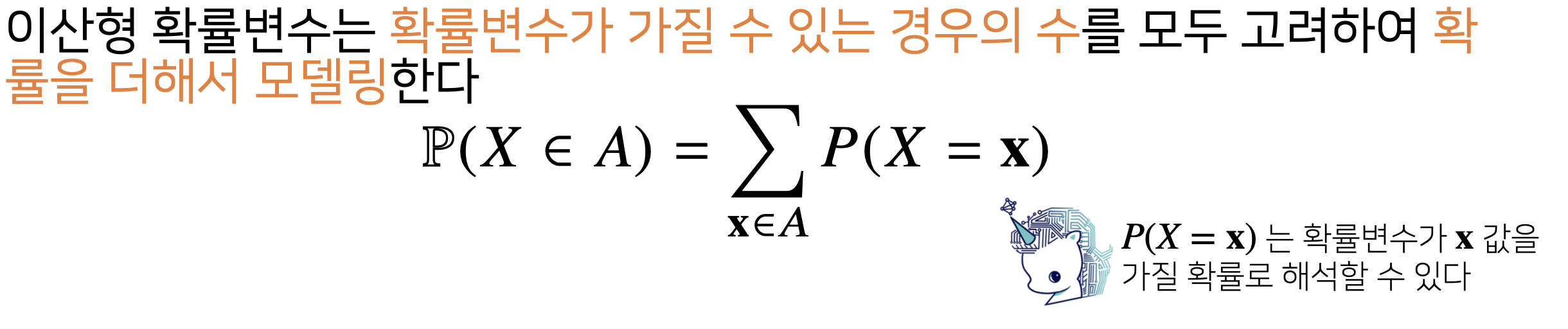
- 정의: 이산 확률변수의 각 가능한 값에 대한 확률을 나타내는 함수

2) 연속 확률변수 (Continuous Random Variable)

값이 연속적(연속된 범위 내의 값)인 경우
- 예: 특정 지역의 기온, 사람의 키
확률밀도함수(PDF, Probability Density Function)가 사용됨
- 정의: 연속 확률변수가 특정 값 근처의 값을 가질 "가능성"을 나타내는 함수.
- PDF의 값 자체는 확률이 아니며, 특정 구간에 대한 확률을 구하려면 PDF를 해당 구간에 대해 적분해야 함.
- 즉, 특정 값 근처의 가능성 밀도를 제공. 특정 값에 대한 확률을 제공하지는 않음.

(참고) 이산확률변수, 연속확률변수 둘 다 아닌 확률변수도 존재함.

(참고) 이러한 확률 분포는 데이터 공간 𝒳×𝒴가 아닌, 데이터 분포 𝒟에 의해 결정됨
그 이유는 데이터 공간 𝒳×𝒴는 입력과 출력의 가능한 모든 조합을 포함하지만, 각 조합이 나타날 확률을 제공하지 않기 때문이다. 반면, 데이터 분포 𝒟는 이러한 조합들이 실제로 어떻게 분포되어 있는지, 즉 각 입력-출력 쌍이 나타날 확률을 제공한다. 따라서, 데이터의 실제 분포와 그 특성을 이해하기 위해서는 데이터 공간 𝒳×𝒴뿐만 아니라, 데이터 분포 𝒟가 필요하다.

확률변수 간의 관계

1) 결합분포(Joint Distribution)

결합 분포 𝑃(𝑋,𝑌)는 우리가 실제로 관찰하는 데이터가 어떻게 입력과 출력의 쌍으로 나타나는지를 설명하는 모델입니다. 이는 데이터가 어떤 방식으로 분포되어 있는지를 이해하는 데 중요합니다.

정의: 두 개 이상의 확률변수가 동시에 특정 값을 가질 확률을 나타내는 분포
표현: 𝑃(𝑋=𝑥, 𝑌=𝑦) $P(X \cap Y)$
활용: 여러 확률변수 간의 상관관계를 이해하는 데 사용됨
원래 확률분포 형태(ex. 이산, 연속)에 상관없이 결합분포 형태(ex. 이산, 연속) 다양하게 가능
결합분포 𝑃(𝑋,𝑌)는 확률분포 𝒟를 모델링함.
- 결합 분포 𝑃(𝑋,𝑌)가 실제 데이터가 어떻게 분포되어 있는지를 설명하는 확률 분포 𝒟를 나타낸다.
- 확률분포 𝒟와 주어진 데이터에서 실증적으로 분포 추정한 값이 다를 수도 있음.
  그래도 근사하는 방법을 찾는 것이 우리의 임무!
예시: 두 개의 주사위를 던지는 실험에서, 𝑋와 𝑌가 각각 두 주사위의 눈을 나타내는 확률변수라고 하자.
이 때 𝑋와 𝑌의 결합분포는 다음과 같이 표현됨:
𝑃(𝑋=𝑥, 𝑌=𝑦) 𝑥, 𝑦 = (1, 2, 3, 4, 5, 6); 주사위 값
- 𝑃(𝑋=1, 𝑌=2)는 첫 번째 주사위가 1이고 두 번째 주사위가 2일 확률임
- 만약 두 주사위가 독립적이라면: 𝑃(𝑋=𝑥, 𝑌=𝑦) = 𝑃(𝑋=𝑥)⋅𝑃(𝑌=𝑦)

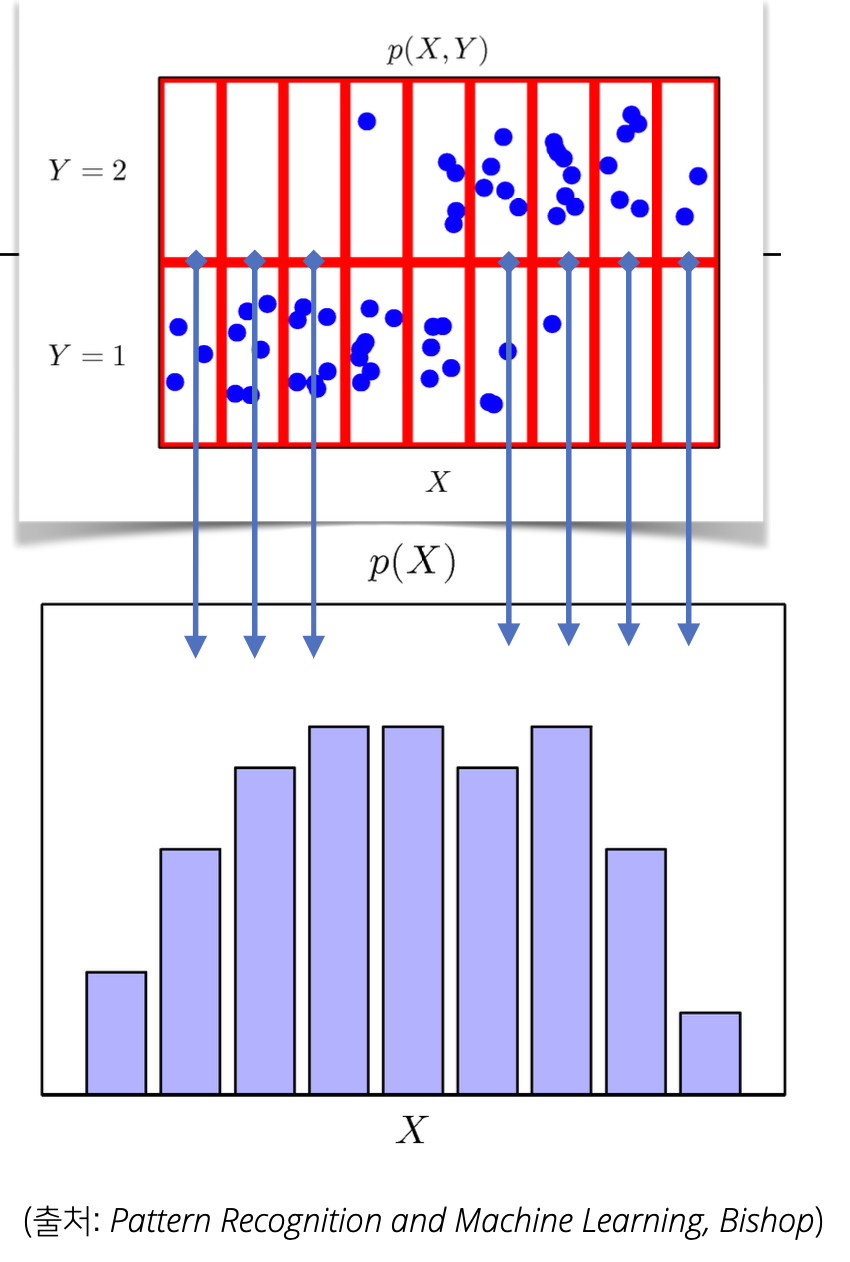
2) 주변확률분포 (Marginal Distribution)

정의: 다변량 확률 분포에서 특정 변수의 분포를 다른 변수와 상관없이 계산한 확률분포 (특정 변수 하나만 고려한 분포)
표현: 𝑃(𝑋=𝑥) = $\Sigma_{y}$ 𝑃(𝑋=𝑥,𝑌=𝑦)
결합확률분포와의 관계: 결합확률분포를 각각의 𝑦에 대해 더해주거나 적분하여 유도함.
𝑋에 대한 정보는 주지만 𝑦에 대한 정보는 주지 않는다는 특징이 있음.
예시: 위의 예에서 주사위 𝑋의 주변확률분포: 주사위 𝑌의 값에 관계없이 𝑋가 특정 값을 가질 확률
활용
- 변수의 단독 분포 분석: 주변 확률 분포는 특정 변수의 분포를 단독으로 분석할 때 사용된다. 이는 변수가 전체 데이터에서 어떻게 분포되어 있는지를 이해하는 데 도움이 된다.
- 독립성 테스트: 두 변수 X와 Y가 독립인지 테스트할 때 사용된다. 만약, X와 Y가 독립이라면, 다음과 같은 식이 성립한다. 𝑃(𝑋,𝑌) = 𝑃(𝑋) * 𝑃(𝑌)
- 베이즈 정리에서의 확률 계산 단순화: 베이즈 정리 $P(A|B) = \frac{P(B|A) * P(A)}{P(B)}$ 에서 $P(B)$ 는 주변확률로, 이 값은 주변확률분포를 통해 얻게 된다.

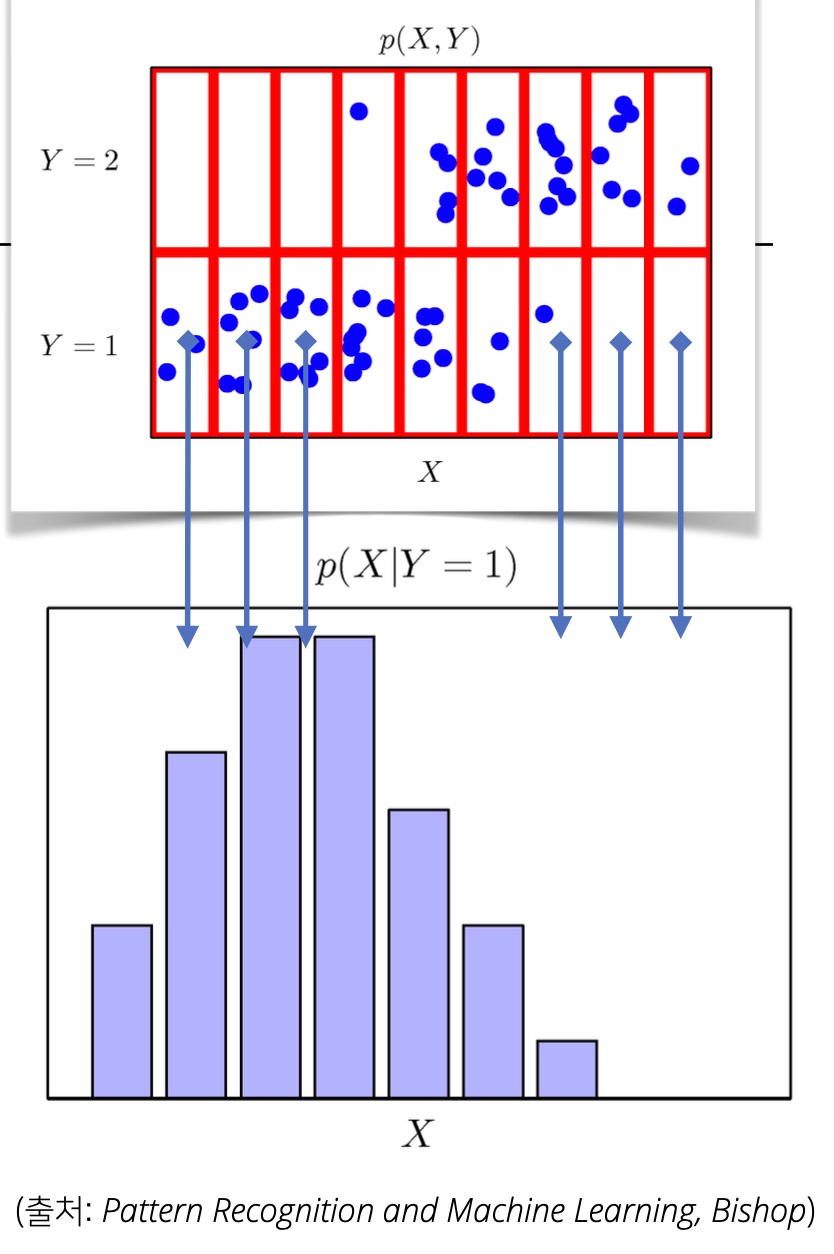
3) 조건부확률분포 (Conditional Distribution)

정의: 입력변수 𝑋에 대해 정답이 𝑦일 확률
표현: 𝑃(𝑌 ∣ 𝑋)
주변확률분포와의 관계: 주변확률분포는 y값에 상관없이(y=1,2) P(X)를 구했다면, 조건부확률분포는 특정 경우(y=1)만 counting함
활용: 주어진 class에 대해 X의 분포가 어떻게 형성되어 있는지 각각 살펴볼 때 사용
- GAN
- Hidden Markov Models: HMM은 현재상태 $S_{t}$ 가 이전 상태 $S_{t-1}$ 에 조건부로 의존한다고 가정함. $P(S_{t}|S_{t-1})$
예시: 위의 예에서 주사위 𝑋가 3이라는 값을 가졌을 때, 주사위 𝑌가 특정 값을 가질 조건부확률

조건부확률과 기계학습

1) 분류 문제: Softmax

소프트맥스 함수는 각 클래스 $y_{i}$ 에 대해 다음과 같은 조건부 확률 $P(y_{i}|x)$ 를 계산

(참고) 구체적인 과정
1. 특징 추출: 입력 데이터 𝑥로부터 특징 패턴 𝜙(𝑥)를 추출합니다.

𝑥: 입력 데이터. 분류 문제에서 예측하고자 하는 특징(feature)들을 포함하는 벡터
추출된 특징패턴 𝜙(𝑥): 입력 데이터 𝑥에서 추출된 특징. 이는 원래 데이터 𝑥를 변환하거나 가공한 결과.

2. 선형 결합: 특징 패턴 𝜙(𝑥)에 가중치 행렬 𝑊를 곱하고 편향 𝑏를 더하여 선형 결합을 만듦.
𝑧 = 𝑊𝜙(𝑥) + 𝑏

가중치 행렬 𝑊: 모델이 학습한 가중치들을 포함하는 행렬. 각 특징에 대한 가중치를 나타냄.
편향 𝑏: 각 클래스에 대한 상수를 포함하는 벡터. 모델의 예측을 조정하는 역할.

3. 소프트맥스 함수: 이 선형 결합 𝑧에 소프트맥스 함수를 적용하여 각 클래스에 속할 확률을 계산.
$softmax(z_{i}) = \frac{e^{z_{i}}} {\sum_{j}e^{z_{j}}}$

2) 회귀 문제: 조건부기대값

조건부기대값 𝐸[𝑦∣𝑥]는 주어진 입력 𝑥에 대해 출력 𝑦의 평균을 의미
이는 𝑥라는 조건 하에서 𝑦가 어떤 값을 가질지의 평균값을 나타냄

보통 회귀문제는 주로 𝑦가 연속적인 값이므로, 확률 밀도 함수(적분)를 통해 𝑦의 평균값을 계산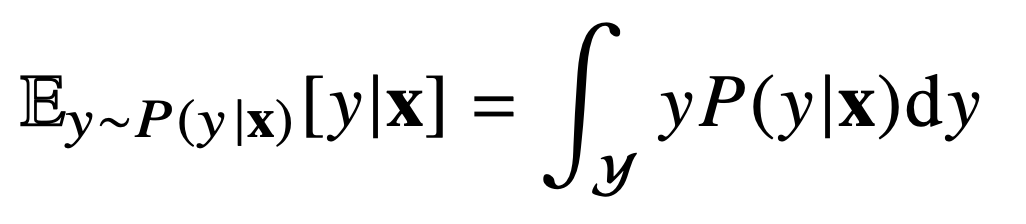

(참고) 조건부기대값과 손실함수의 관계
주어진 𝑥에 대해 손실 함수 $∥𝑦−𝑓(𝑥)∥_{2}$ 를 최소화하는 최적의 함수 𝑓(𝑥)는 바로 조건부 기대값 $𝐸[y|x]$ 입니다. 즉, 다음과 같은 관계가 성립합니다: 𝑓(𝑥)=𝐸[𝑦∣𝑥]

직관적 이해: 회귀 분석에서 모델이 예측하고자 하는 값은 주어진 입력 𝑥에 대해 출력 𝑦의 평균값입니다. 평균 제곱 오차를 최소화하는 것이 모델의 목표인 경우, 최적의 예측값은 실제 출력값의 평균이 됩니다. 이를 수학적으로 표현한 것이 𝑓(𝑥)=𝐸[𝑦∣𝑥] 입니다.

(참고) 기대값이란?

몬테카를로 샘플링

배경
기계학습의 많은 문제들은 확률분포를 명시적으로 모를 때가 대부분이다.
이런 경우, 현재 가지고 있는 데이터를 이용해 기대값을 계산하기 위해서는 몬테카를로(Monte Carlo) 샘플링 방법을 사용해야 한다.

반복된 무작위 추출을 이용하여 함수의 값을 근사하는 알고리즘을 의미한다.
확률변수가 상호독립적일 때, 모두 동일한 확률분포를 가진다면 기대값을 랜덤하게 뽑은 n개 샘플의 평균치와 유사하다! (당연히 N이 커질수록 더욱 유사해짐)
출처: https://think-tech.tistory.com/29 [자윰이의 성장일기:티스토리]