[2024.03.19] 백트래킹 응용 & 그래프(트리)

• 병합정렬

# 병합 정렬
# 분할 정복 기법을 통해서 동작하는 정렬 방식

def merge_sort(arr):
    # 기저조건(종료조건): 배열의 요소가 2개 미만이라면 종료
    if len(arr) < 2:
        return

    # Divide(분할 단계): arr 배열을 절반씩 나누어서 최소 배열이 될 때까지 반복
    mid = len(arr) // 2
    # 왼쪽 배열, 오른쪽 배열로 나누기 (슬라이싱)
    left_arr, right_arr = arr[:mid], arr[mid:]

    # Conquer(정복 단계): 정렬이 완수된 왼쪽 배열과 오른쪽 배열을 각각 재귀적으로 진행
    merge_sort(left_arr)
    merge_sort(right_arr)

    # Combination(결합 단계): 정렬된 왼쪽 배열과 오른쪽 배열을 병합하여 정렬된 새로운 배열을 만든다
    # 병합을 진행할 미리 할당할 요소 크기만큼 정적으로 생성
    merge_arr = arr
    # 병합 배열의 인덱스 변수 k
    k = 0
    # 왼쪽 배열과 오른쪽 배열 각각의 인덱스 변수 l, r
    l = r = 0

    # 왼쪽 배열의 요소가 비거나 또는 오른쪽 배열의 요소가 비거나 할 때까지 반복
    while len(left_arr) > l and len(right_arr) > r:
        # 왼쪽 배열의 요소와 오른쪽 배열의 요소를 비교
        if left_arr[l] < right_arr[r]:
            merge_arr[k] = left_arr[l]
            l += 1
        else:
            merge_arr[k] = right_arr[r]
            r += 1
        k += 1

    # 남은 요소를 병합 배열에 추가
    # while len(left_arr) > l:
    #     merge_arr[k] = left_arr[l]
    #     l += 1
    #     k += 1
    if len(left_arr) > l:
        merge_arr[k:] = left_arr[l:]

    # while len(right_arr) > r:
    #     merge_arr[k] = right_arr[r]
    #     r += 1
    #     k += 1
    if len(right_arr) > r:
        merge_arr[k:] = right_arr[r:]


arr = [3, 33, 4, 1, 8, 9, 43]
merge_sort(arr)
print(arr)

백트래킹 응용

• 백트래킹: 완전 탐색(재귀) + 가지치기
  => 가능성이 없는(볼 필요 없는) 경우의 수를 제거하는 기법

• 재귀함수: 특정 시점으로 돌아오는 게 핵심!

• 파라미터(인자): 바로 작성하지 않고, 구조를 먼저 잡으면 자연스럽게 필요한 변수들이 보인다!

ex) 중복된 순열 (1~3 숫자 배열)
: 111,112,113,121,122,123, ... ,332,333

arr = [i for i in range(1, 4)]
visited = [0] * 3

def dfs(level):
    # 기저조건
    if level == 3:
        print(*visited)
        return

    # 다음 재귀 호출
    # -> 다음에 갈 수 있는 곳들은 어디인가?
    # -> 이 문제에서는 1, 2, 3 세 가지(arr의 길이만큼) 경우의 수가 존재
    # 기본 ver.
    # visited[level] = 1
    # dfs(level+1)
    #
    # visited[level] = 2
    # dfs(level+1)
    #
    # visited[level] = 3
    # dfs(level+1)

    # 반복문 ver.
    for i in range(len(arr)):
        # 여기는 못 가! (가지치기)
        if arr[i] in visited:
            continue
        visited[level] = arr[i]
        dfs(level + 1)
        # 갔다와서 할 로직
        visited[level] = 0

dfs(0)

arr = [i for i in range(1, 11)]
visited = [0] * 10

def dfs(level, start):
    # 기저조건
    if sum(visited) == 10:
        #print(*visited)
        print([i for i in visited if i != 0])
        return

    # 가지치기
    if sum(visited) > 10:
        return

    for i in range(start, len(arr)):
        # 가지치기
        if visited[i] != 0:
            continue
        visited[i] = arr[i]
        dfs(level+1, i+1)
        # 갔다와서 할 로직
        visited[i] = 0

dfs(0, 0)

# 부분집합의 합이 target과 같아졌을 때 출력하는 함수
def find_subset_with_total(arr, target):
    # arr배열의 부분집합을 만드는 재귀함수
    def find_subsets(arr, target, total, depth, subset):
        # 나의 목표(target)와 현재 합(total)이 같아졌을 때 출력
        if target == total:
            print(subset)
            return

        # 가지치기: 현재까지의 부분집합 합이 목표(target)을 넘어서는 경우
        if target < total:
            return

        # 기저조건 (종료조건): 모든 원소를 다 탐색한 경우
        if depth == len(arr):
            return

        # 재귀호출: 현재 원소(depth의 인덱스에 해당)를 추가하는 경우
        subset.append(arr[depth])  # 결정
        find_subsets(arr, target, total + arr[depth], depth + 1, subset)
        subset.pop()  # 복구

        # 현재 원소를 추가하지 않는 경우
        find_subsets(arr, target, total, depth + 1, subset)

    # 재귀함수를 실행하기 위한 초기값 설정 후 호출
    subset = []
    find_subsets(arr, target, 0, 0, [])


# A 전체 집합을 선언
A = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
# 목표로 하는 합이 10인 경우, 모두 출력
find_subset_with_total(A, 10)

트리 개요

• 트리는 싸이클이 없는 무향 연결 그래프이다.
  -두 노드(or 정점) 사이에는 유일한 경로가 존재한다.
  -각 노드는 최대 하나의 부모 노드가 존재할 수 있다.
  -각 노드는 자식 노드가 없거나 하나 이상이 존재할 수 있다.

• 비선형 구조
  -원소들 간에 1:n 관계를 가지는 자료구조
  -원소들 간에 계층관계를 가지는 계층형 자료구조

• 한 개 이상의 노드로 이루어진 유한 집합이며 다음 조건을 만족한다.

  1. 노드 중 부모가 없는 노드를 루트(root)라고 한다.
  2. 나머지 노드들은 n(>=0)개의 분리 집합 T1,...,TN으로 분리될 수 있다.

• 이들 T1,...,TN은 각각 하나의 트리가 되며(재귀적 정의), 루트의 서브트리(subtree)라 한다.
  
  
  
  
  

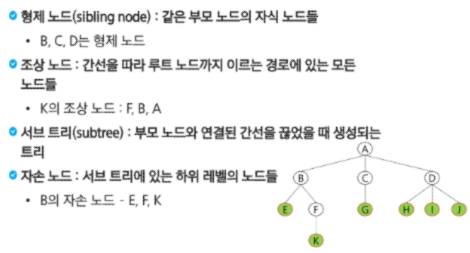
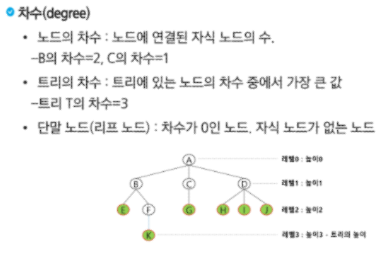
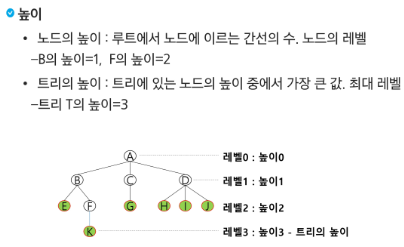
이진 트리

• 이진 트리(Binary Tree)
  : 모든 노드들이 최대 2개의 서브 트리를 갖는 특별한 형태의 트리. 각 노드가 자식 노드를 최대 2개까지만 가질 수 있는 트리(왼쪽 자식 노드 & 오른쪽 자식 노드)
  

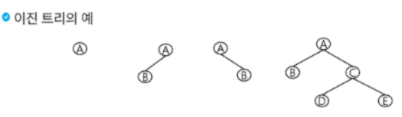
• 이진 트리의 특성
  -레벨 i에서의 노드의 최대 개수는 2^i개
  -높이가 h인 이진 트리가 가질 수 있는 노드의 최소 개수는 (h+1)개가 되며, 최대 개수는 (2^h+1-1)개가 된다.
  

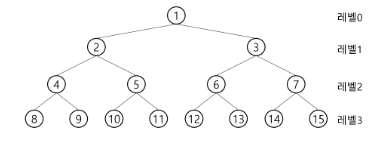
• 노드 개수 N개일 때, 이진 트리 높이 h는?
  최악의 경우: 높이 h = N / 최선의 경우: 높이 h = logN

• 포화 이진 트리(Full Binary Tree)
  : 모든 레벨에 노드가 포화상태로 채워져 있는 이진 트리

• 완전 이진 트리(Complete Binary Tree)
  : 높이가 h이고 노드 수가 n개일 때, 포화 이진 트리의 노드 번호 1번부터 n번까지 빈 자리가 없는 이진 트리

• 편향 이진 트리(Skewed Binary Tree)
  : 높이 h에 대한 최소 개수의 노드를 가지면서 한쪽 방향의 자식 노드만을 가진 이진 트리

arr = [1, 2, 1, 3, 2, 4, 3, 5, 3, 6, 4, 7, 5, 8, 5, 9, 6, 10, 6, 11, 7, 12, 11, 13]

nodes = [[] for _ in range(14)]
for i in range(0, len(arr), 2):
    parent_node = arr[i]
    child_node = arr[i+1]
    nodes[parent_node].append(child_node)

#자식이 없음을 표시하기 위해 None
for li in nodes:
    for _ in range(len(li), 2):
        li.append(None)

#중위순회 구현
def inorder(nodeNum):
    #갈 수 없다면 skip
    if nodeNum == None:
        return
    #왼쪽으로 갈 수 있다면 진행
    inorder(nodes[nodeNum][0])
    print(nodeNum, end=' ')
    #오른쪽으로 갈 수 있다면 진행
    inorder(nodes[nodeNum][1])

inorder(1)

이진 탐색 트리 (BST)

• 이진 탐색 트리
  -탐색 작업을 효율적으로 하기 위한 자료구조
  -모든 원소는 서로 다른 유일한 키를 갖는다.
  -key(왼쪽 서브 트리) < key(루트 노드) < key(오른쪽 서브 트리)
  -왼쪽 서브 트리와 오른쪽 서브 트리도 이진 탐색 트리다.
  -중위 순회하면 오름차순으로 정렬된 값을 얻을 수 있다.
  

• 탐색 연산의 횟수는 트리의 높이 !! (=> log N ~ N)

힙 트리 (Heap)

• 완전 이진 트리에 있는 노드 중에서 키 값이 가장 큰 노드나 키 값이 가장 작은 노드를 찾귀 위해 만든 자료구조
  -최대 힙(max heap): 키 값이 가장 큰 노드를 찾기 위한 완전 이진 트리 => 부모 노드의 키 값 > 자식 노드의 키 값
  -최소 힙(min head): 키 값이 가장 작은 노드를 찾기 위한 완전 이진 트리 => 부모 노드의 키 값 < 자식 노드의 키 값

n-queen

#중첩함수: 내부함수를 만들어서 간단하게 정리
def nqueen_solve(n):
    def check(row, col):
        # 이전까지 놓아져있는 퀸이 (x,y)
        for x in range(row):
            y = board[x]
            # 내가 놓으려는 (row, col)의 위치와 대각선 영역이 서로 겹치는가?
            if abs(x - row) == abs(y - col):
                return False  # 놓을 수 없음
        return True

    #완전탐색
    def dfs(depth):
        nonlocal count, visited, board
        #기저조건: depth가 퀸 개수만큼 카운트 되었을 때 => 중단
        if depth == n:
            count += 1 #퀸이 올바르게 배치되어 있는 경우 카운트 + 1
            return

        #재귀적으로 말을 배치
        #반복문을 통해 1부터 8번까지의 모든 위치에 말을 놓아보자
        for col in range(n):
            if not visited[col] and check(depth, col):
                board[depth] = col
                #visited 배열을 통해 동일한 행에 대해 다른 퀸이 들어가지 않도록 체크
                visited[col] = True
                dfs(depth + 1)
                visited[col] = False

    count = 0
    visited = [False] * n
    board = [-1] * n
    dfs(0)

    return count

n = int(input())
ans = nqueen_solve(n)
print(ans)