Intro: 알고리즘 설계 기법의 종류
-
전체를 그냥 다 보자. (Brute-Force; 완전 탐색)
-배열: for문, while문
-그래프(관계가 있는 데이터): DFS, BFS
-> 완전 탐색을 구현하면, 시간 or 메모리 초과가 되더라! -
상황마다 좋은 걸 고르자. (Greedy; 그리디)
-규칙 + 증명 -> 구현 -
큰 문제를 작은 문제로 나누어 부분적으로 해결하자. (Dynamic Programming; 동적 프로그래밍)
-분할 정복과 다르게 작은 문제가 중복
-중복된 문제의 해답을 저장해놓고 재활용하자.(Memoization) -
큰 문제를 작은 문제로 나누어 부분적으로 해결하자. (Divide and Conquer; 분할 정복)
-
전체 중 가능성 없는 것을 빼자. (Backtracking; 백트래킹)
=> 이 기본들을 기반으로 더 고급 알고리즘들이 개발됨.
분할 정복
- 설계 전략:
- 분할(Divide): 해결할 문제를 여러 개의 작은 부분으로 나눈다.
- 정복(Conquer): 나눈 작은 문제를 각각 해결한다.
- 통합(Combine): (필요하다면) 해결된 해답을 모은다.
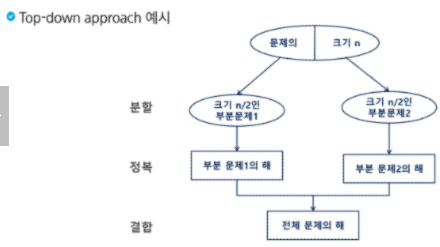
대표적인 분할 정복 알고리즘
병합 정렬
-
병합 정렬(Merge Sort)
: 여러 개의 정렬된 자료의 집합을 병합하여 한 개의 정렬된 집합으로 만드는 방식 -
특징
외부 정렬의 기본이 되는 정렬 알고리즘이다.
멀티코어 CPU나 다수의 프로세서에서 정렬 알고리즘을 병렬화하기 위해 병합 정렬 알고리즘이 활용된다. -
분할 정복 알고리즘 활용
: 자료를 최소 단위의 문제까지 나눈 후에 차례대로 정렬하여 최종 결과를 얻어냄. (top-down 방식) -
시간 복잡도: O(n log n)
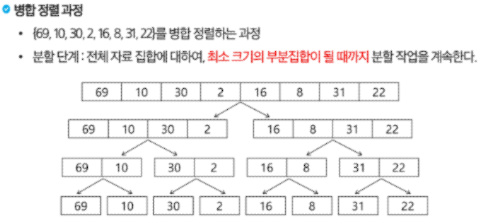
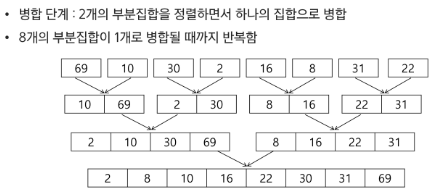

=> O(log n)

=> O(n)
퀵 정렬
-
퀵 정렬(Quick Sort)
: 주어진 배열을 두 개로 분할하고, 각각을 정렬한다. -
특징
: 평균적으로 효율이 굉장히 좋다. (큰 데이터 정렬 시 특히 효율적) -
병합 정렬과 다른 점
- 병합 정렬은 그냥 두 부분으로 나누는 반면, 퀵 정렬은 분할할 때, 기준 아이템(pivot item) 중심으로 분할한다.
-기준보다 작은 것은 왼편, 큰 것은 오른편에 위치시킨다. - 각 부분 정렬이 끝난 후, 병합정렬은 "병합"이란 후처리 작업이 필요하나, 퀵 정렬은 필요로 하지 않는다.

- Hoare-Partition 알고리즘

- 정렬 방식

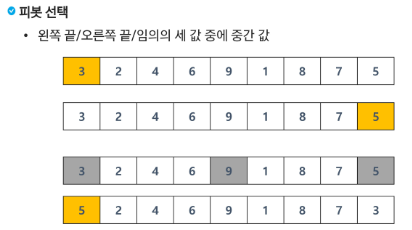
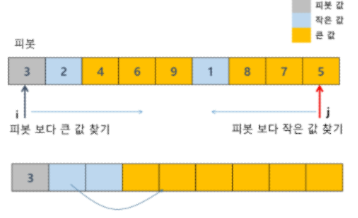
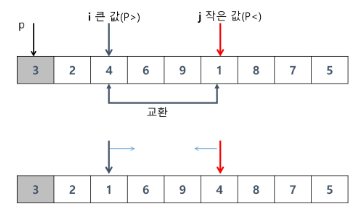
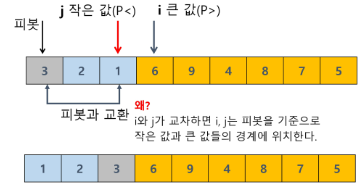
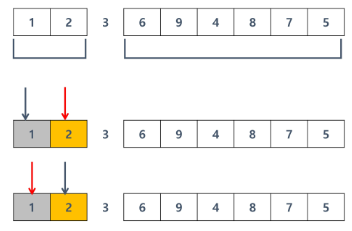
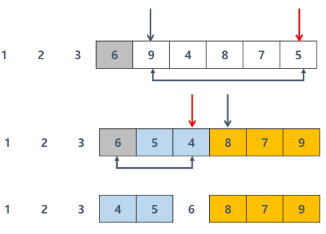
# 퀵 소트는 분할 정복 기법에 의해 동작한다
# 중간값(pivot)을 기준으로 왼쪽은 작은 값, 오른쪽은 큰 값을 만드는 과정을 진행
# 병합 정렬은 후처리로 하여금, 요소를 재정렬하는 과정이 추가적으로 진행되지 않음 (추가 메모리 공간 사용 x)
# 중간값 pivot을 뽑고, 그 pivot을 중심으로
# 왼쪽은 작은 값, 오른쪽은 큰 값을 만들어줘야 한다.
def partition(arr, l, r):
# pivot값 뽑기
pivot = arr[l]
# 두 인덱스의 이동 경로 i ----> <---- j 이동 경로
i, j = l, r
# 이 i, j의 인덱스가 서로 교차될 때까지 반복 수행
while i <= j:
# i 인덱스는 오른쪽으로 이동 (pivot값보다 큰 값이 있다면 중단)
while i <= j and arr[i] <= pivot:
i += 1
# j 인덱스는 왼쪽으로 이동 (pivot값보다 작은 값이 있다면 중단)
while i <= j and arr[j] >= pivot:
j -= 1
# i 인덱스가 j 인덱스보다 작을 때만 교체
# i 인덱스와 j 인덱스가 가리키는 요소를 교환 (swap)
if i < j:
arr[i], arr[j] = arr[j], arr[i]
# pivot과 중간의 값을 교체
arr[l], arr[j] = arr[j], arr[l]
return j # pivot의 위치를 반환
def quick_sort(arr, l, r):
if l < r:
# partitioning을 진행하고, pivot 값이 있는 s를 가져온다
s = partition(arr, l, r)
# 분할정복 기법: 왼쪽 리스트와 오른쪽 리스트를 다시 정렬 수행
quick_sort(arr, l, s-1)
quick_sort(arr, s+1, r)
arr = [11, 45, 23, 81, 28, 34]
quick_sort(arr, 0, len(arr)-1)
print(arr)
arr = [11, 45, 22, 81, 23, 34, 99, 22, 17, 8]
quick_sort(arr, 0, len(arr)-1)
print(arr)
arr = [1, 1, 1, 1, 1, 0, 0, 0, 0, 0]
quick_sort(arr, 0, len(arr)-1)
print(arr)- Lomuto partition 알고리즘 (Hoare보다 조금 더 안 좋음)


이진 검색 (중요!)
-
이진 검색(Binary Search)
: 자료의 가운데에 있는 항목의 키 값과 비교하여 다음 검색의 위치를 결정하고 검색을 계속 진행하는 방법. 목적 키를 찾을 때까지 이진 검색을 순환적으로 반복 수행함으로써 검색 범위를 반으로 줄여가면서 보다 빠르게 검색을 수행함.
*이진 검색을 하기 위해서는 자료가 정렬된 상태여야 한다. -
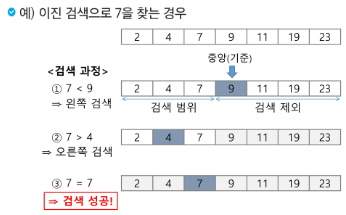
검색 과정
- 자료의 중앙에 있는 원소를 고른다.
- 중앙 원소의 값과 찾고자 하는 목표 값을 비교한다.
- 목표 값이 중앙 원소의 값보다 작으면 자료의 왼쪽 반에 대해서 새로 검색을 수행하고, 크다면 자료의 오른쪽 반에 대해서 새로 검색을 수행한다.
- 찾고자 하는 값을 찾을 때까지 1~3의 과정을 반복한다.


arr = [324, 32, 22113, 16, 48, 93, 422, 21, 316]
# 1. 정렬
arr.sort()
# 2. 이진 검색 - 반복문 버전
def binarySearch(target):
# 제일 왼쪽, 오른쪽 인덱스 구하기
low = 0
high = len(arr) - 1
# 탐색 횟수
cnt = 0
# 해당 숫자를 찾으면 종료
# 더 이상 쪼갤 수 없을 때까지 반복
while low <= high:
mid = (low + high) // 2
cnt += 1
if arr[mid] == target:
return mid, cnt
elif arr[mid] > target:
high = mid - 1
elif arr[mid] < target:
low = mid + 1
# 못 찾았으면 -1 반환
return -1, cnt
print(binarySearch(21))
print(binarySearch(324))
print(binarySearch(888))
arr = [324, 32, 22113, 16, 48, 93, 422, 21, 316]
# 1. 정렬
arr.sort()
low = 0
high = len(arr) - 1
# 2. 이진 검색 - 재귀 버전
def binarySearch(low, high, target):
# 기저조건
if low > high:
return -1
# 정답 판별
mid = (low + high) // 2
if target == arr[mid]:
return mid
# 다음 재귀 함수 호출
if target < arr[mid]:
return binarySearch(low, mid-1, target)
else:
return binarySearch(mid+1, high, target)
print(binarySearch(0, len(arr)-1, 21))
print(binarySearch(0, len(arr)-1, 324))
print(binarySearch(0, len(arr)-1, 888))*추가적으로 이진 검색의 Lower Bound, Upper Bound 개념 공부하기!
