[코드트리] 트로미노

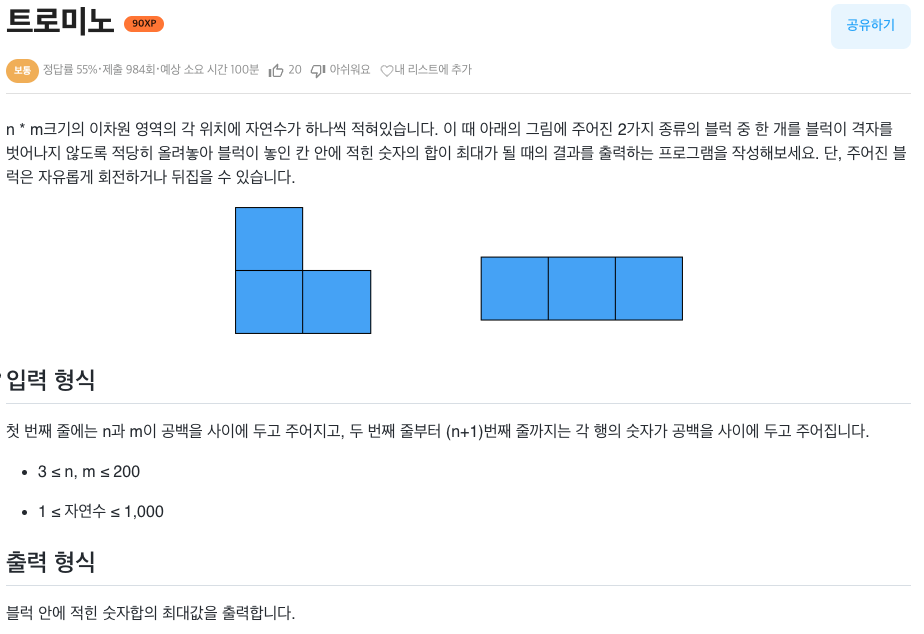
문제

• https://www.codetree.ai/missions/2/problems/tromino?utm_source=clipboard&utm_medium=text

해결방법

• n과 m의 범위는 3 이상 200이하, 격자 내 부분합 최댓값 및 시간복잡도가 O(NM)으로 풀림 => 완전탐색 기법 사용
• 주어진 격자 "ㄴ" 자와 "ㅡ"자는 회전이 가능하다 => 총 6개의 모양이 나옴
• 관건은 6개의 모양을 어떻게 구하느냐

Idea 1. "ㄴ" 자의 회전 => 사각형에서 좌표값 하나 빼주기 방식으로 접근

• ㄴ자가 예를 들어 (row, col) 기준 (0,0), (1,0), (1,1)로 이루어져 있다고 가정하자.
• 이는 (0,0), (1,0), (0,1), (1,1) 에서 (0,1) 만 빠지는 것이다.
• 마찬가지로 ㄴ자에서 반시계 방향으로 180도 돌린 ㄱ자 모양은 (1,0)만 빠진 것이다.
• 이렇게 ㄴ자가 회전하는 4가지 경우는, 사각형 (0,0), (1,0), (0,1), (1,1)의 좌표값의 합에서 하나씩 빼주는 것과 동일하다. => 반복문을 통해 구현

코드

#include <iostream>
#include <climits>
#include <algorithm>

#define MAX_N 200
#define MAX_M 200

using namespace std;

int n, m;
int arr[MAX_N][MAX_M];

// 의자모양 회전시킬 때 사용하는 dx, dy
int dx[4] = {0, 0, 1, 1};
int dy[4] = {0, 1, 0, 1};

int main() {

    cin >> n >> m;
    int maximum = INT_MIN;

    // 입력
    for(int i = 0; i < n; i++) {
        for(int j = 0; j < m; j++) {
            cin >> arr[i][j];
        }
    }
    // 우선 의자모양 블록(회전 경우의 수 포함)
    for(int i = 0; i < n-1; i++) {
        for(int j = 0; j < m-1; j++) {
            // 사각형 모두 선택
            int tmp_max = 0;
            for(int k = 0; k < 4; k++) {
                int x = i + dx[k];
                int y = j + dy[k];
                tmp_max += arr[x][y];
            }
            // 회전 코드 => 사각형을 이루고 있는 좌표들 중 하나 빼 주는 방식을 통해 4개의 경우의 수 모두 구함
            for(int k = 0; k < 4; k++) {
                int x = i + dx[k];
                int y = j + dy[k];
                tmp_max -= arr[x][y];
                maximum = max(maximum, tmp_max);
                tmp_max += arr[x][y];

            }
        }
    }

    // 막대모양(가로)
    for(int i = 0; i < n ; i++) {
        for(int j = 0; j < m-2; j++) {
            int tmp_max = arr[i][j] + arr[i][j+1] + arr[i][j+2];
            maximum = max(maximum, tmp_max);

        }
    }

    // 막대모양(세로)
    for(int j = 0; j < m; j++) {
        for(int i = 0; i < n-2 ; i++) {
            int tmp_max = arr[i][j] + arr[i+1][j] + arr[i+2][j];
            maximum = max(maximum, tmp_max);
        }
    }

    cout << maximum;
    return 0;
}

개선 방향

• 아래와 같이 6개의 경우의 수를 모두 구해, 반복문을 통해 범위가 벗어나지 않으면서 shapes의 원소값이 1인 위치만 더해서 구할 수 있다.

int shapes[6][3][3] = {
    {{1, 1, 0},
    {1, 0, 0},
    {0, 0, 0}},

    {{1, 1, 0},
    {0, 1, 0},
    {0, 0, 0}},

    {{1, 0, 0},
    {1, 1, 0},
    {0, 0, 0}},

    {{0, 1, 0},
    {1, 1, 0},
    {0, 0, 0}},

    {{1, 1, 1},
    {0, 0, 0},
    {0, 0, 0}},

    {{1, 0, 0},
    {1, 0, 0},
    {1, 0, 0}},
};