[딥러닝] Neural Networks & Multi-Layer Perceptron

Neural Networks

• 신경망은 동물의 뇌를 구성하는 생물학적 신경망에서 막연하게 영감을 받은 컴퓨팅 시스템이다.

Linear Neural Networks

• Data : N개의 1차원 x, 1차원 y가 모여있다.
• Model : x에 w라는 스칼라를 곱하고 b라는 bias를 더해서 모델이 만들어진다. x에서 $\hat y$으로 가는 mapping을 찾는게 목적인데 이것을 선형으로 한정짓고 선형 모델을 정의하는 w와 b를 찾는게 모델링이다.
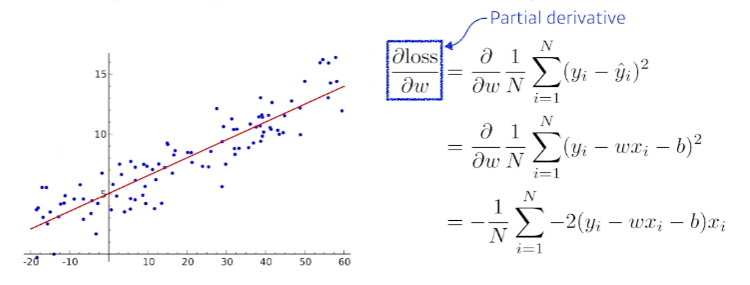
• Loss : 정답(y)와 추측값($\hat y$)의 차이. 여기서는 MSE를 사용하였다.

• w와 b 즉, 파라미터를 찾는 방법은 굉장히 다양하다. 선형으로 문제를 만들고 위와같이 Squared error(MSE 등)를 사용하게 되면 모델이 linear하고 데이터가 단순한 w와 b에 대해서는 단순하게 최적값을 찾을 수 있다.
• 하지만 차원이 늘어나면 단순히 찾을 수 없다. 따라서 loss를 줄이는 게 목적이므로 parameter가 어느 방향으로 움직였을 때 loss가 줄어드는지를 찾고 그 방향으로 parameter를 바꾸는게 우리의 목표이다. loss가 줄어드는것이 목적이므로 loss fucntion을 각각 parameter로 미분하게 되는 방향의 음수방향으로 parameter를 업데이트 하게 되면 loss가 최소화 되는 지점을 찾을 수 있게 된다.

• 새로운 w = 기존의 w값 - $\eta$(step size) $\times$ ${\partial loss}\over\partial w$(편미분값)
• 새로운 b = 기존의 b값 - $\eta$(step size) $\times$ ${\partial loss}\over\partial b$(편미분값)

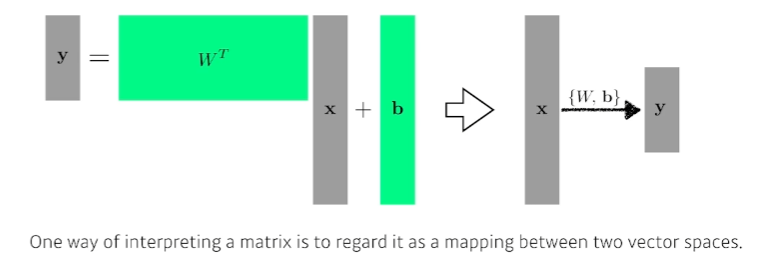
• affine transform : 행렬을 곱함으로써 차원을 조정할 수 있다. (4,4) @ (4,2) = (4,2)

• 행렬을 곱하는 것에 대한 해석 : 두개의 vector space의 변환. 선형성을 가지는 변환이 있을 때 그 변환은 항상 행렬로 표현된다.

• 행렬을 찾는다 : 두개의 vector space 혹은 두 서로다른 차원 사이의 선형 변환을 찾는것

• x라는 입력을 w와b를 통해 y로 출력하는것

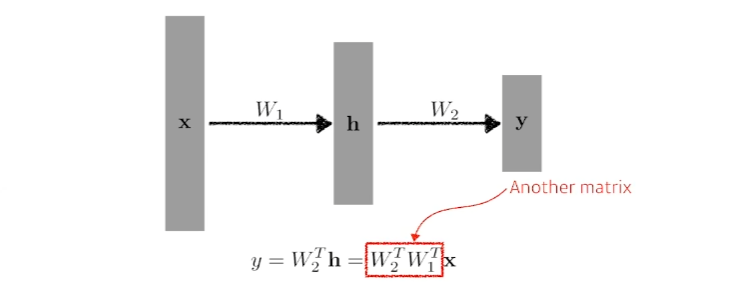
-네트워크를 여러개 쌓기 위해서 $x$를 $W_1$를 통해 나오는 벡터를 $h$라고 하고, $h$를 또다시 $W_2$를 곱해준다. 하지만 이렇게 되면 결국 두개의 행렬곱에 지나지 않기 때문에 이것은 한단짜리 뉴럴네트워크와 다를게 없다.

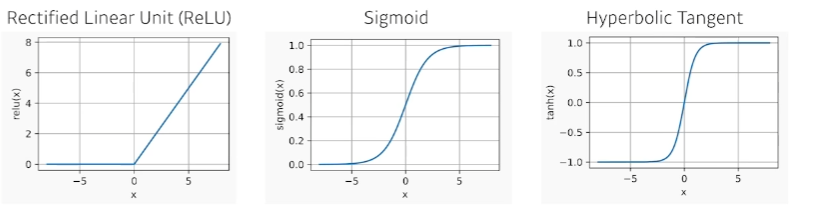
• 그렇기 때문에 우리는 중간에 Nonlinear transform이 필요하다. 단순히 선형 변환을 n번 반복하는것이 아니라, 한번 선형 변환이 이루어지게 되면 그 뒤에 activation fucntion을 통해 nonlinear transform을 거치고 그렇게 얻게 되는 feature vector를 다시 변환하는것을 반복한다. 이것을 n번 반복하면 더 많은 표현력을 갖게 되는 것이다.

• Activation function의 종류 : ReLu, sigmoid 등