.png)
Tree 구조란?
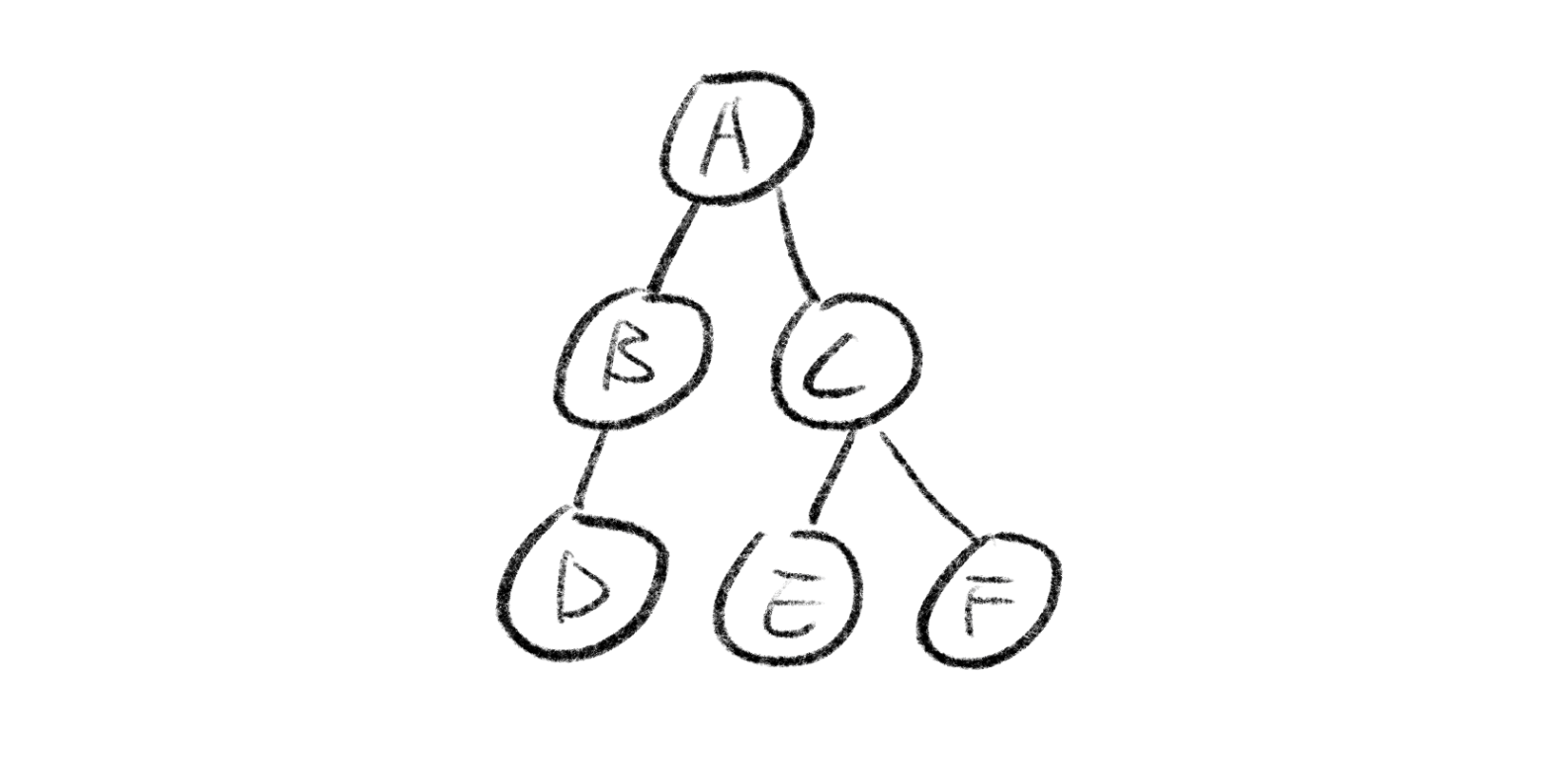
- 나무의 가지가 뻗은 구조처럼 생긴 자료구조이다.
→ 근데 이제 거꾸로 뒤집어버린 단방향 그래프의 일종으로, 하나의 데이터에 하나 이상의 데이터가 연결된 계층적 구조이다.- 데이터를 순차적으로 연결시킨 것이 아니기 때문에,
비선형구조라고 불린다.
노드
- 트리 구조에서의 각 데이터를
노드(Node)라고 하며, 이때 트리구조의 시작점이 되는 노드를루트(Root)라고 한다.
→ 위의 그림에선 A가 루트이다. - 각 노드가 서로 상하관계로 연결되어 있을 때, 루트에 가까운 것을
부모노드(Parent Node), 먼것을자식노드(Child Node)라고 한다.
→ 위에서 각각B는D의,C는EF의 부모노드이다. - 자식노드가 없는 트리구조의 마지막 노드들을
리프(Leaf)라고 한다.
→ 나뭇잎, 위에선DEF가 이에 해당한다.
깊이
- 각 노드가 루트로 부터 얼마나 떨어져있는 지를
깊이(Depth)로 표현하며, 루트를 기준으로 0부터 시작하여 결정된다.
→A의 깊이는 0이며,DEF의 깊이는 2가 된다.
레벨
- 여기서 같은 깊이를 가지고 있는 요소들을
레벨(Level)로 묶을 수 있으며, 깊이가 0인A의 레벨은 1, 깊이가 1인BC의 레벨은 2 가 된다. - 이때, 같은 레벨을 가진 노드들을
형제노드(Sibling Node)라고 한다.
높이
높이(Height)는 깊이의 반대되는 개념으로 루트를 기준으로 하는 깊이와는 다르게, 리프 노드의 위치를 0으로 기준으로 정한다.
→ 가장 바닥부터- 위의 경우
EFG의 높이는 0이고,A의 높이는 2가 된다.
서브트리
- 트리구조 내부에 또 다른 트리구조를 가진 데이터를 서브트리(Sub Tree)라고 한다.
- 여기선
CEF를 서브트리라고 부를 수 있다.
이진 트리
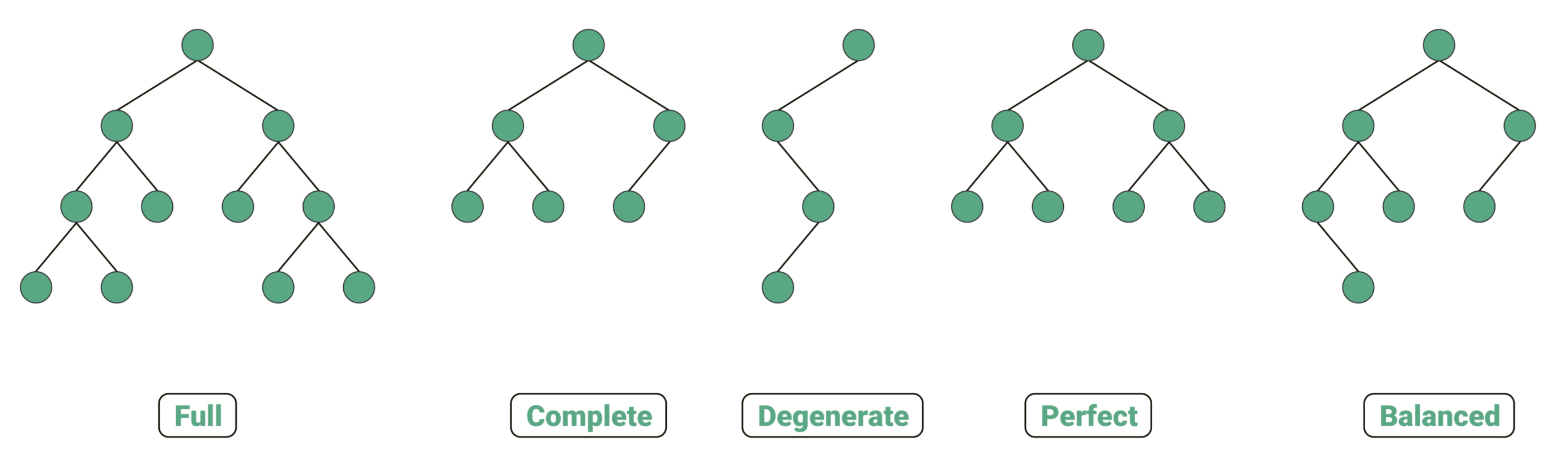
- 각각 정 이진 트리, 완전 이진 트리, 퇴화 이진 트리, 포화 이진 트리, 균형 이진 트리
- 정, 포화, 완전만 살펴보자.
이진 트리란?
- 자식 노드의 수가 최대 두개로 이루어진 트리구조
- 두개의 자식노드를
왼쪽 자식노드와오른쪽 자식노드로 구분 할 수 있다.
→ 0, 1과 같아 이진트리 - 특성으로는 왼쪽 자식의 값이 루트나 부모보다 작고, 오른쪽 자식의 값은 루트나 부모보다 크다는 특성을 가진다.
정 이진 트리
- 각 노드가 0개 혹은 2개의 자식 노드를 가진다.
포화 이진 트리
- 모든 노드가 2개의 자식 노드를 가진다.
- 모든 노드가 2개의 자식 노드를 가지므로, 리프 노드의 레벨이 전부 동일하며, 전부 채워져있다.
- 정 이진 트리의 특성과 중복된다.
완전 이진 트리
- 마지막 레벨을 제외한 모든 노드들이 존재해야 한다.
- 마지막 레벨의 왼쪽의 노드가 전부 존재해야한다.
→ 오른쪽 노드는 전부 존재하지 않아도 됨
트리의 순회
- 트리순회는 3가지의 방법으로 나뉜다.
https://hongku.tistory.com/160
→ 순회의 순서에 대한 정리가 잘 되어 있다.
전위순회(Preorder Traversal)
- 루트부터 확인하여 왼쪽의 노드를 전부 탐색하고 오른쪽 노드를 탐색한다.
- 루트(부모) 노드 → 왼쪽 자식 노드 → 오른쪽 자식 노드
중위순회
- 루트를 기준으로 왼쪽의 노드부터 탐색하며, 왼쪽의 노드 탐색이 끝나면 오른쪽 노드의 탐색을 시작한다.
- 이때 루트는 전체 트리의 루트 뿐만 아니라, 서브트리의 루트 또한 기준으로 한다.
- 왼쪽 자식 노드 → 루트(부모) 노드 → 오른쪽 자식 노드
(가장 왼쪽의 노드부터 탐색한다고 생각하면 된다.)
후위순회
- 루트를 가장 마지막에 탐색한다.
- 루트를 지나쳐 왼쪽 노드를 먼저 탐색하고, 곧바로 오른쪽 노드를 탐색한 뒤에 루트를 탐색하고 다음 트리로 넘어간다.
- 왼쪽 자식 노드 → 오른쪽 자식 노드 → 루트(부모) 노드
+
- 이진 트리의 탐색방법은 술게임 업다운으로 생각해보면 이해가 빠르다.
