간단한 신경망 만들기

3.1 보스턴 집값 예측하기 : 회귀 분석

특징feature

• 결과를 예측하는데 사용되는 데이터 요소

특징에 모델의 가중치를 반영해 결과를 도출한다.
집값만을 예측하기 때문에 하나만 출력

평가지표 : 평균 제곱 오차(MSE)

3.1.1 데이터 살펴보기

from sklearn.datasets import load_boston

# 경고 무시
import warnings
warnings.filterwarnings('ignore')

dataset = load_boston() # ❶ 데이터셋을 불러옴
print(dataset.keys())   # 데이터셋의 키(요소들의 이름)를 출력

data : 특징값
target : 예측할 값. 정답
feature_names : 각 특징 이름
DESCR : description의 약자. 데이터셋에 대한 전반적인 정보를 제공
filename : 데이터셋의 csv 파일이 존재하는 위치

3.1.2 데이터 불러오기

import pandas as pd

from sklearn.datasets import load_boston

dataset = load_boston()
dataFrame = pd.DataFrame(dataset["data"]) # ❶ 데이터셋의 데이터 불러오기
dataFrame.columns = dataset["feature_names"] # ❷ 특징의 이름 불러오기
dataFrame["target"] = dataset["target"] # ❸ 데이터 프레임에 정답을 추가

dataFrame.head() # ➍ 데이터프레임을 요약해서 출력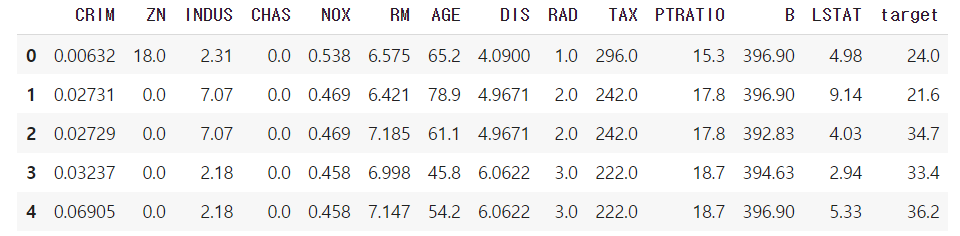

3.1.3 모델 정의 및 학습하기

선형회귀에 의해 얻은 결과를 실제 데이터와 비교해 오차를 줄여나가는 방식으로 학습한다.

평균 제곱 오차Mean Square Error, MSE를 사용한다.

평균 제곱 오차(MSE)

• 오차에 제곱을 취하고 평균을 낸 값
• MSE를 사용하면 작은 오차와 큰 오차를 강하게 대비시킬 수 있어 유용

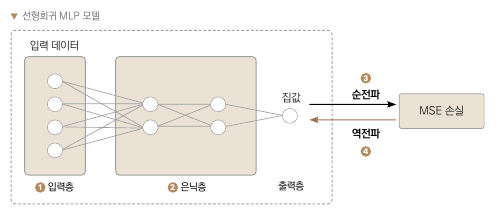
윗 그림은 선형회귀에 이용할 다층 신경망(MLP) 모델 그림
MLP층은 각 층의 뉴런이 다음 층의 모든 뉴런과 연결되어 있다(완전연결층fully connected layer, FC)

❶ 입력층에 입력 데이터가 들어온다.
❷ 은닉층에 전달된 입력 데이터의 특징에서 정보 추출
❸ 출력층의 예측값과 실제 정답을 비교해서 손실 계산
➍ 손실이 계산됐으면 가중치를 수정하기 위해 오차를 역전파한다.

신경망을 만들기 위해선, 배치와 에포크 개념을 알아야 한다.
컴퓨터 메모리는 한정되어 있어 데이터를 한 번에 처리할 수 없다.
따라서 전체 데이터를 나눠서 학습해야 한다.
이때, 떼어서 학습하는 단위가 배치

'배치 크기'만큼 학습해서 전체 데이터를 학습하면 '1에포크'를 학습했다고 한다.

ex) 데이터가 총 1,000개일 때, 배치 크기가 100이면,
배치가 10번 반복되어야, 1에포크의 학습이 이루어진다.

ex) 100 에포크를 학습한다면,
데이터 1,000개 모두를 사용하는 학습을 100번 반복

이때 반복 횟수를 이터레이션이라고 한다.

import torch
import torch.nn as nn

from torch.optim.adam import Adam


# ❶ 모델 정의

# torch.nn.Sequential() 객체에 모듈(여기서는 선형 회귀 모듈)을 집어넣어주면, 
파이토치가 알아서 순서대로 계산
# 선형 회귀 모델이기에 nn.Linear 모듈 사용


model = nn.Sequential(
   nn.Linear(13, 100),
   nn.ReLU(),
   nn.Linear(100, 1)
) 

X = dataFrame.iloc[:, :13].values # ❷ 정답을 제외한 특징을 X에 입력
Y = dataFrame["target"].values    # 데이터프레임의 target의 값을 추출

batch_size = 100
learning_rate = 0.001

# ❸ 가중치를 수정하기 위한 최적화 정의
optim = Adam(model.parameters(), lr=learning_rate)


# 에포크 반복
for epoch in range(200):

   # 배치 반복
   for i in range(len(X)//batch_size):
       start = i*batch_size      # ➍ 배치 크기에 맞게 인덱스를 지정
       end = start + batch_size


       # 파이토치 실수형 텐서로 변환
       x = torch.FloatTensor(X[start:end])
       y = torch.FloatTensor(Y[start:end])

       optim.zero_grad() # ❺ 가중치의 기울기를 0으로 초기화
       preds = model(x)  # ❻ 모델의 예측값 계산
       loss = nn.MSELoss()(preds, y) # ❼ MSE 손실 계산
       loss.backward() # ❽ 오차 역전파
       optim.step() # ❾ 최적화 진행

   if epoch % 20 == 0:
       print(f"epoch{epoch} loss:{loss.item()}")

# ❶ 모델 정의

# torch.nn.Sequential() 객체에 모듈(여기서는 선형 회귀 모듈)을 집어넣어주면, 
파이토치가 알아서 순서대로 계산
# 선형 회귀 모델이기에 nn.Linear 모듈 사용


model = nn.Sequential(
   nn.Linear(13, 100),
   nn.ReLU(),
   nn.Linear(100, 1)
) 

❶ 신경망 모델 정의
nn.Sequential()에 입력된 층들이 순서대로 계산.
nn.Linear()와 nn.ReLU()만을 사용했는데,
Linear()는 MLP 모델을 의미
ReLU()는 활성화 함수의 일종

Linear(13, 100)에서 13은 입력 차원, 100은 출력 차원
(13개의 특징을 받아 100개의 특징을 반환한다)

※ 이전 층의 출력과 층의 입력이 일치하지 않으면 에러가 발생

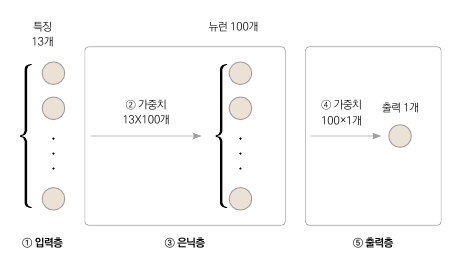
① 입력층에 특징 13개
③ 은닉층은 뉴런 100개로 구성되어 있으므로
② 가중치는 13 x 100개(입력 특징 개수 x 은닉층 뉴런 개수)가 필요
⑤ 출력층은 하나의 출력값만 사용하므로
④ 가중치는 100 x 1개(은닉층 뉴런 개수 x 출력값 개수)가 필요

X = dataFrame.iloc[:, :13].values # ❷ 정답을 제외한 특징을 X에 입력
Y = dataFrame["target"].values    # 데이터프레임의 target의 값을 추출

❷ dataFrame에서 target을 제외한 나머지 값을 X에 입력
dataFrame의 요소들은 특징의 이름으로 호출해야 한다.
만약, 일산화탄소 농도에 대한 데이터를 불러오려면 dataFrame에 "일산화탄소"라는 문자열을 넣어줘야 한다.
하지만, iloc을 이용해 특징들의 위치로 호출할 수 있게 해준 뒤, 정답을 제외한 모든 데이터를 불러온다.

# ❸ 가중치를 수정하기 위한 최적화 정의
optim = Adam(model.parameters(), lr=learning_rate)

❸ Adam()은 가장 많이 쓰이는 최적화 기법

최적화 기법

• 역전파된 오차를 이용해 가중치를 수정하는 기법
• 대표적으로 Adam과 경사 하강법

최적화가 필요한 모델의 가중치들과 학습률을 입력으로 받는다.

Adam(params, lr)

• 학습률 lr을 갖고, 모델 가중치(params)에 대해 Adam 최적화를 해주는 객체

   # 배치 반복
   for i in range(len(X)//batch_size):
       start = i*batch_size      # ➍ 배치 크기에 맞게 인덱스를 지정
       end = start + batch_size


       # 파이토치 실수형 텐서로 변환
       x = torch.FloatTensor(X[start:end])
       y = torch.FloatTensor(Y[start:end])

➍ 전체 데이터를 배치 크기(batch_size)로 나누고, 시작 지점(i*batch_size)과 끝나는 지점(start + batch_size)을 계산한다.
FloatTensor()을 사용해서 자료형을 실수형으로 변환

FloatTensor(A)

• 객체 A를, 실수값을 갖는 파이토치 텐서로 변환

       optim.zero_grad() # ❺ 가중치의 기울기를 0으로 초기화

❺ 최적화를 실행하기 전, 모든 기울기 0으로 초기화
이전 배치에서 계산된 기울기가 남아 있기 때문에 배치마다 초기화해준다.

       preds = model(x)  # ❻ 모델의 예측값 계산

❻ 모델에 입력 데이터를 넣는다.

       loss = nn.MSELoss()(preds, y) # ❼ MSE 손실 계산

❼ nn.MSELoss()는 평균 제곱 오차MSE
실제값과 예측값의 차이를 제곱하고, 모든 입력에 대해 평균을 내는 오차

MSELoss(Xpreds, target)

• preds와 target에 대한 제곱 평균 오차를 구하는 함수

       loss.backward() # ❽ 오차 역전파

❽ loss.backward()는 오차를 역전파시킬 기울기 저장
❼에서 계산한 오차를 역전파
이 과정에서 모든 가중치에 대한 기울기 계산

       optim.step() # ❾ 최적화 진행

❾ optim.step()은 최적화 함수에 맞춰 오차 역전파 수행
❽에서 역전파된 기울기를 이용해 최적화 진행.
이때 얼마만큼 가중치를 수정할 지 결정

3.1.4 모델 성능 평가하기

prediction = model(torch.FloatTensor(X[0, :13]))
real = Y[0]
print(f"prediction:{prediction.item()} real:{real}")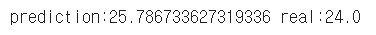

실제 집값은 24.0이지만,
모델이 예측한 집값은 25.7
더 정확한 결과를 얻고 싶다면 데이터 전처리를 이용해 모든 특징의 범위를 동일하게 하는 등의 추가 조작이 필요하다.

3.2 손글씨 분류하기 : 다중분류

다중출력

• 모델 하나로 여러 정보 예측

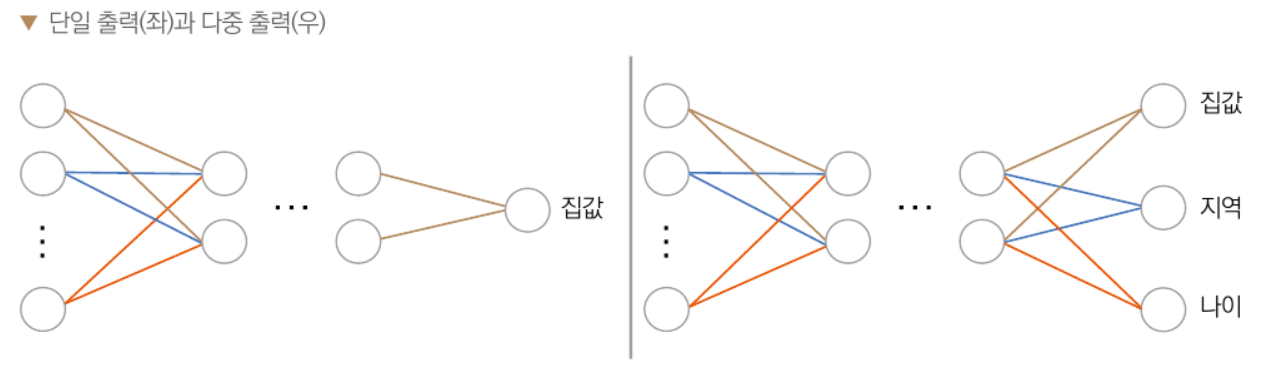
회귀와 분류는 값을 직접 예측하느냐, 어떤 범주에 들어가느냐의 문제이므로 서로 관련이 없어보이나,
신경망의 출력을 그대로 사용하면 회귀,
출력을 확률 분포로 바꿔주면 분류 문제가 된다.

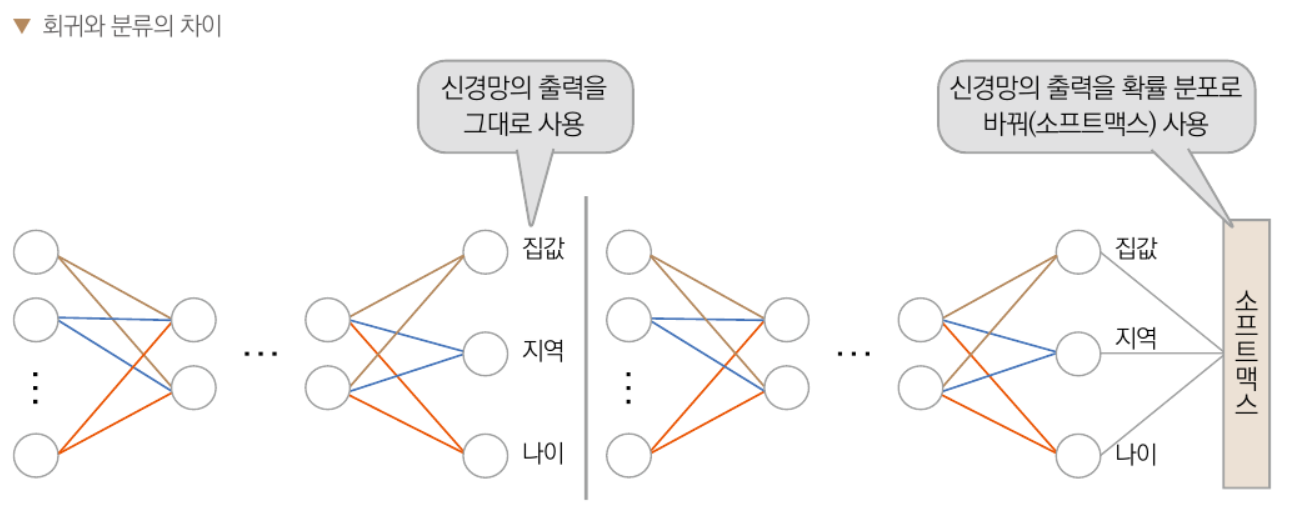
회귀, 분류 모델은 신경망 구조가 완전히 동일하나,
분류 모델은 최종적으로 출력을 소프트맥스 함수를 통해 확률 분포로 변환
∵ 출력값의 범위를 0~1 사이로 제한해야 해석이 용이

평가지표 : CE 오차

3.2.1 데이터 살펴보기

import matplotlib.pyplot as plt

from torchvision.datasets.mnist import MNIST
from torchvision.transforms import ToTensor

# ❶ 학습용 데이터와 평가용 데이터 분리
training_data = MNIST(root="./", train=True, download=True, transform=ToTensor())
test_data = MNIST(root="./", train=False, download=True, transform=ToTensor())


print(len(training_data)) # 학습에 사용할 데이터 개수
print(len(test_data))     # 평가에 사용할 데이터 개수

for i in range(9): # 샘플 이미지를 9개 출력
   plt.subplot(3, 3, i+1)
   plt.imshow(training_data.data[i])
plt.show()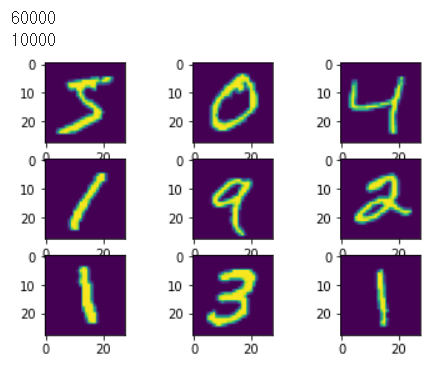

학습에 사용할 데이터 개수,
평가에 사용할 데이터 개수,
9개의 샘플 이미지 출력

MNIST 객체를 초기화 할 때, train=True는 학습용, train=False는 평가용 데이터를 불러온다.

download 옵션은 데이터를 내려받을지 결정하는 파라미터

transform은 데이터를 변형하고 싶을 때 넣어주는 파라미터
파이토치는 최적화가 굉장히 복잡하게 정의되어 있어, 자료형이 다르면 동작 불가능.
모든 데이터가 파이썬 이미지 파일로 저장되어 있기에, ToTensor()함수를 이용해 파이토치 텐서로 변환
∵ 파이토치 모델의 입력으로는 파이토치 텐서만을 입력으로 받는다.

3.2.2 데이터 불러오기

Dataloader(A)

• 학습에 사용할 배치를 자동으로 반환하는 파이토치 메서드
• 원하는 배치 크기, 데이터 셔플 여부, CPU 코어 사용 갯수 등을 지정

from torch.utils.data.dataloader import DataLoader

train_loader = DataLoader(training_data, batch_size=32, shuffle=True)

# ❶평가용은 데이터를 섞을 필요가 없음
test_loader = DataLoader(test_data, batch_size=32, shuffle=False) 

학습용 데이터를 섞지 않고 학습하면, 하나의 범주만을 출력하도록 학습될 가능성이 있다.
ex. 학습용 데이터의 첫 6,000장의 이미지가 0을 나타낸다면, 모델은 계속해서 0을 출력하기에, 나중에 어떤 값이 들어와도 0이 나온다.

평가용 데이터는 이미 학습이 된 모델을 이용하여 순서대로 예측값과 정답을 비교하는 과정이기에 데이터를 섞을 필요가 없다.

3.2.3 모델 정의 및 학습하기

이미지 학습에 드는 계산량이 크므로 GPU 사용

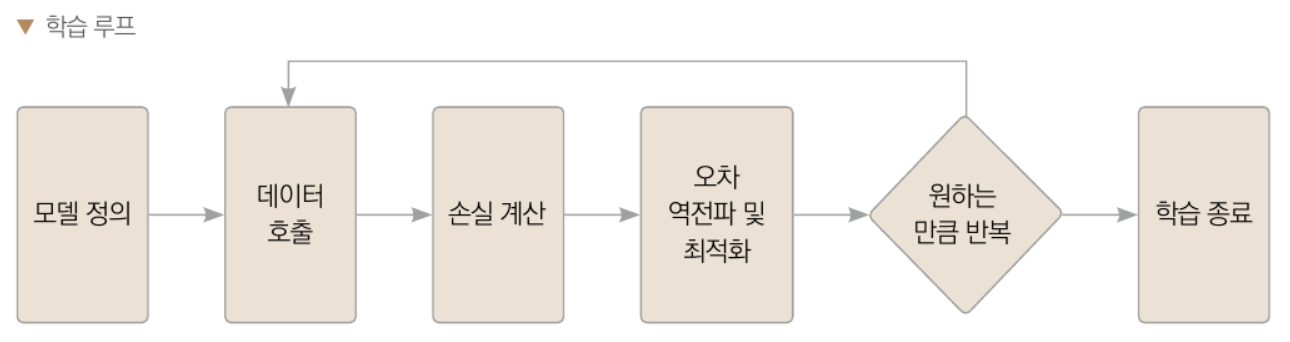
이미지는 가로축과 세로축으로 이루어진 2차원 데이터이나,
인공 신경망은 일렬 배열을 입력으로 갖는다.
따라서 1차원으로 모양을 변경해야 한다.

import torch
import torch.nn as nn

from torch.optim.adam import Adam

device = "cuda" if torch.cuda.is_available() else "cpu" # ❶ 학습에 사용할 프로세서를 지정

model = nn.Sequential(
   nn.Linear(784, 64),
   nn.ReLU(),
   nn.Linear(64, 64),
   nn.ReLU(),
   nn.Linear(64, 10)
)
model.to(device) # 모델의 파라미터를 GPU로 보냄

lr = 1e-3
optim = Adam(model.parameters(), lr=lr)

for epoch in range(20):
   for data, label in train_loader:
       optim.zero_grad()
       # ❷ 입력 데이터를 모델의 입력에 맞게 모양을 변환
       data = torch.reshape(data, (-1, 784)).to(device)
       preds = model(data)

       loss = nn.CrossEntropyLoss()(preds, label.to(device)) # ❸ 손실 계산
       loss.backward()
       optim.step()

   print(f"epoch{epoch+1} loss:{loss.item()}")

torch.save(model.state_dict(), "MNIST.pth") # ➍ 모델을 MNIST.pth라는 이름으로 저장

device = "cuda" if torch.cuda.is_available() else "cpu" # ❶ 학습에 사용할 프로세서를 지정

❶ CPU or GPU 선택
torch.cuda.is_available()은 GPU 사용 가능 시 True, 아니면 False

for epoch in range(20):
   for data, label in train_loader:
       optim.zero_grad()
       # ❷ 입력 데이터를 모델의 입력에 맞게 모양을 변환
       data = torch.reshape(data, (-1, 784)).to(device)
       preds = model(data)

❷ 이미지 일렬 변환 실행
(-1, 784)의 -1은 개수를 상관하지 않겠다는 뜻
MNIST의 이미지는 28x28(784픽셀) 흑백 이미지이므로, 채널에 관한 정보는 없다.
따라서 높이x너비 모양으로, -1을 입력하면 배치 크기 입력됨.
ex. 이미지 64장이면, 입력 텐서는 (64, 28, 28)
이때 (-1, 784)로 이미지를 일렬로 정렬
-1로, 배치 크기인 64가 대입되어
최종적으로 (64, 784)와 같은 모양으로 변환

MLP 모델은 벡터만 입력 받을 수 있기 때문에,
손글씨 이미지를 벡터로 변환해준다.

device가 다른 두 텐서는 서로 연산이 불가능하기 때문에 모든 텐서의 device를 맞춰야한다.

reshape(A, shape)

• 텐서 A를 shape 모양으로 변형시킨다.

       loss = nn.CrossEntropyLoss()(preds, label.to(device)) # ❸ 손실 계산
       loss.backward()
       optim.step()

❸ 손실 함수 정의
회귀에는 MSE, 분류에는 CE를 자주 사용

크로스 엔트로피(cross entropy, CE)

• 교차 엔트로피
• 두 확률 분포가 서로 얼마나 다른가를 나타내는 함수

torch.save(model.state_dict(), "MNIST.pth") # ➍ 모델을 MNIST.pth라는 이름으로 저장

➍ save(A) : 객체 A 저장
A.state_dict(pth) : A 모델의 가중치를 딕셔너리 형태로 반환한 뒤,pth에 저장

3.2.4 모델 성능 평가하기

# ❶ 모델 가중치 불러오기
model.load_state_dict(torch.load("MNIST.pth", map_location=device))

num_corr = 0 # 분류에 성공한 전체 개수

with torch.no_grad(): # ❷ 기울기를 계산하지 않음
   for data, label in test_loader:
       data = torch.reshape(data, (-1, 784)).to(device)

       output = model(data.to(device))
       preds = output.data.max(1)[1] # ❸ 모델의 예측값 계산
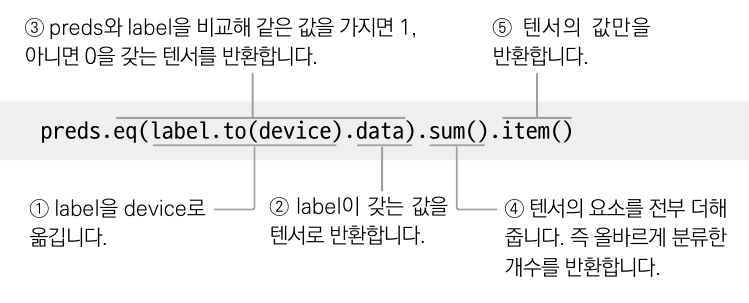
       # ❹ 올바르게 분류한 개수
       corr = preds.eq(label.to(device).data).sum().item()
       num_corr += corr

   print(f"Accuracy:{num_corr/len(test_data)}") # 분류 정확도를 출력합니다.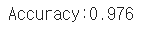

# ❶ 모델 가중치 불러오기
model.load_state_dict(torch.load("MNIST.pth", map_location=device))

num_corr = 0 # 분류에 성공한 전체 개수

❶ 모델 파일 불러오기
map_location은 불러올 위치. 기본은 CPU에서 불러옴

with torch.no_grad(): # ❷ 기울기를 계산하지 않음
   for data, label in test_loader:
       data = torch.reshape(data, (-1, 784)).to(device)

❷ no_grad()는 기울기를 계산하지 않는다.
평가는 가충치를 바꿀 필요가 없기에 기울기 계산을 하지 않는다.
메모리와 계산량이 줄어들기에, 평가 시 반드시 호출

       preds = output.data.max(1)[1] # ❸ 모델의 예측값 계산

❸ max(1)[1]은 가장 높은 값을 갖는 위치 반환
모든 텐서의 차원은 배치, 클래스 순서
max(0)은 배치에서 가장 높은 값을 반환
max(1)은 클래스 차원에서 가장 높은 값을 반환

max()는 최대 예측값, 최대 예측값의 인덱스를 묶어 리스트로 반환
따라서, max(1)[1]로 모든 배치에 대해 가장 높은 클래스값을 갖는 인덱스만 호출

# ❹ 올바르게 분류한 개수
       corr = preds.eq(label.to(device).data).sum().item()
       num_corr += corr

❹ eq()는 값이 같으면 1, 아니면 0을 반환
preds 안에 모델의 예측값이 들어있기에
label과 eq() 연산을 해주고 sum()으로 합을 구한다.
실젯값과 예측값이 몇 개나 일치하는지 확인 가능

일반적으로 92% 이상이면 학습이 잘 이루어진 것으로 판단.
80% 미만이면 모델을 제품화 할 수 없다.