메모이제이션 동적계획법의 필요성

피보나치 수열(Fibonacci numbers) - 1의 $F_N$을 구하는 방법은 동일한 재귀함수를 여러번 호출하기 때문에 $N$이 높아질수록 효율이 극도로 나빠진다.

• $F_5$만 예로 들어봐도 Fibo(3)을 2번, Fibo(2)를 3번 거친다.
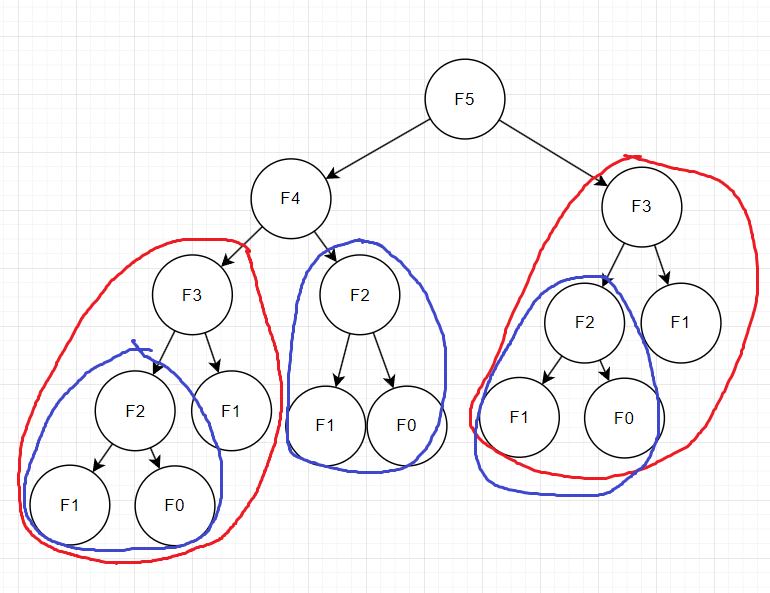  N이 조금만 더 커져도 동일한 인자의 함수 호출 횟수는 엄청나게 늘어난다.

Fibo(N)의 반환 값을 미리 저장해두고, 나중에 동일한 값으로 호출했을 때 저장한 값을 돌려주는 메모이제이션 방법을 사용하면 된다.

구현

코드를 설명하는게 더 나은 것 같아서 바로 코드를 써본다.

#include <iostream>
#include <vector>
using namespace std;

vector<long long> memo;

long long Fibo(int N)
{
    //베이스 케이스
    if (N == 0)
        return 0;
    else if (N == 1)
        return 1;

    if (memo[N] != -1) return memo[N];

    return memo[N] = Fibo(N - 1) + Fibo(N - 2);
}

int main()
{
    memo.assign(50, -1);
    
    cout << "Fibo(49) : " << Fibo(49)<< endl;
}

• 가변 배열 memo는 모두 -1로 초기화를 해준다.
• return memo[N] = Fibo(N - 1) + Fibo(N - 2);를 한 번이라도 거쳤다면
  memo[N]은 -1이 아니므로 또 Fibo(N-1)과 Fibo(N-2)를 호출하는 것이 아닌
  memo[N]에 저장된 값을 반환만 해주면 된다.

---

참고 자료
오츠키 켄스케 , 『문제 해결력을 높이는 알고리즘과 자료구조, 서수환 옮김, 길벗(2022)