TIL 0127 게임개발 입문 팀 과제 - 3

강성원·2024년 1월 28일

TIL 오늘 배운 것

목록 보기

25/69

오늘 개발한 내용

오브젝트 풀링

오늘은 오브젝트 풀링 클래스를 따로 만들어서 뒤섞여있던 기능들을 나누고자 했다.
입문 강의에 나온 오브젝트 풀링 코드가 우리 프로젝트에 사용돼도 적절할 것 같아서 오브젝트 풀링 코드는 그대로 사용하였다.

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class ObjectPool : MonoBehaviour
{
    [System.Serializable]
    public struct Pool
    {
        public string tag;
        public GameObject prefab;
        public int size;
    }

    [SerializeField]
    private List<Pool> pools;
    private Dictionary<string, Queue<GameObject>> poolDictionary;

    private void Awake()
    {

        poolDictionary = new Dictionary<string, Queue<GameObject>>();
        foreach (var pool in pools)
        {
            Queue<GameObject> objectPool = new Queue<GameObject>();
            for (int i = 0; i < pool.size; i++)
            {
                GameObject obj = Instantiate(pool.prefab);
                obj.SetActive(false);
                objectPool.Enqueue(obj);
            }
            poolDictionary.Add(pool.tag, objectPool);
        }
    }

    public GameObject SpawnFromPool(string tag)
    {
        if (!poolDictionary.ContainsKey(tag))
            return null;

        GameObject obj = poolDictionary[tag].Dequeue();
        poolDictionary[tag].Enqueue(obj);

        return obj;
    }


}

문제점

위 오브젝트 풀링 코드를 사용하여 기존의 다른 코드에서 하던 역할을 분리한 것 까지는 좋았는데, 문제는 트랜스폼의 스케일과 로테이션에서 발생했다.

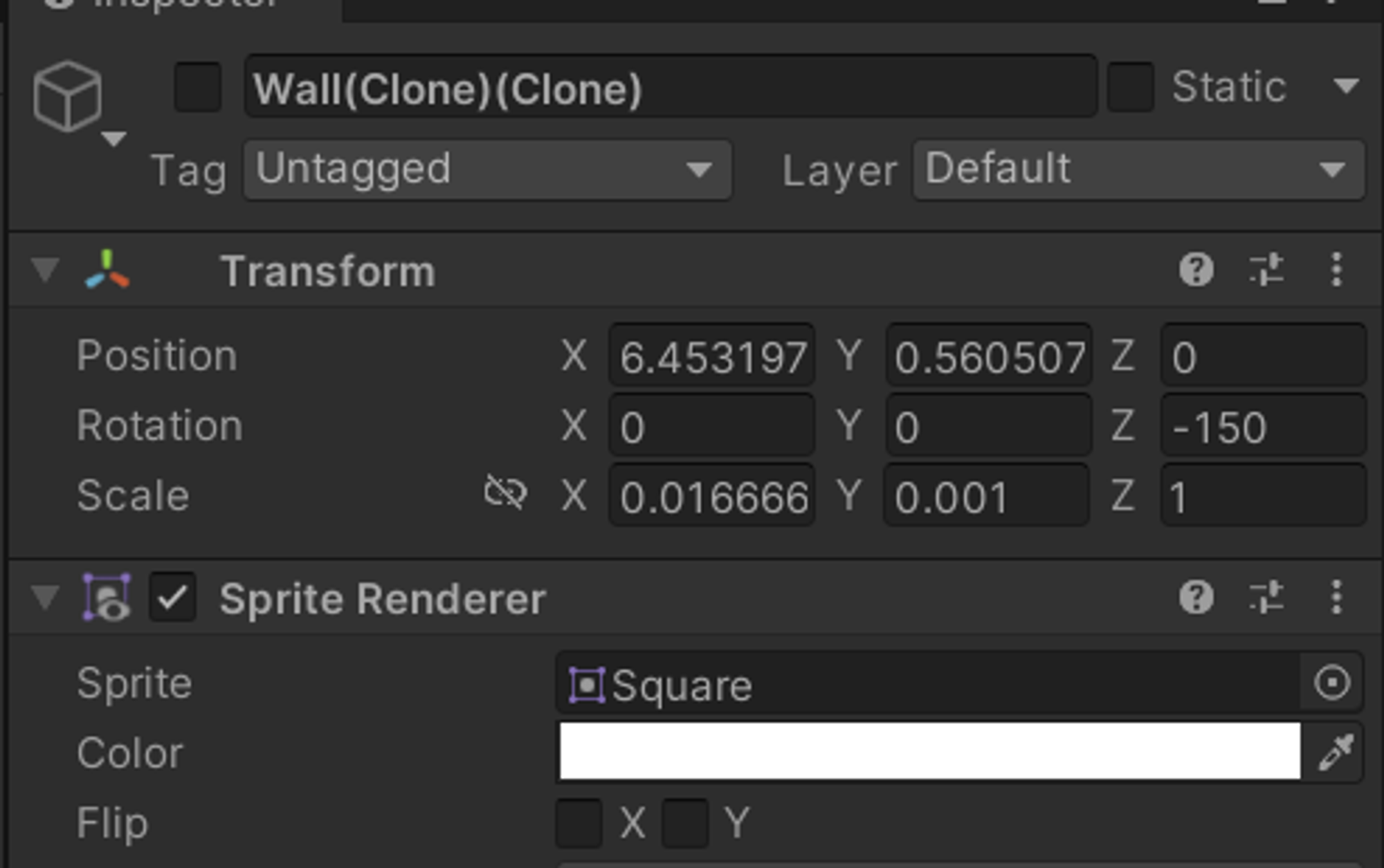매 주기마다 나타나야 하는 "Wall"이 오브젝트 풀링을 통해서 인스턴스화되고 다른 오브젝트(벽을 주기적으로 생성하는 오브젝트, 이하"A")에 자식으로 종속되면 위 사진처럼 크기가 매우 작아지고, z축이 회전돼버린다.

"Wall"프리팹의 Rotation은 (0,0,0)이고 Scale은 (1, 0.06, 1)이다.

아마 오브젝트 풀링 코드에서 인스턴스화 하면 월드 좌표계 상에서 Rotation(0,0,0)/Scale(1, 0.06, 1)이 되고 (=> 원하는 크기보다 한참 작고 회전 값도 다름)
"A"에 종속 시키면 위 사진과 같은 Transform이 나온다.

해결?

결국 "Wall"이 "A"의 자식으로 들어가고 크기와 회전을 원하는 값으로 조정하는 초기화 과정을 거치도록 하였다.

하지만 하드코딩에 가까운 결과물이기 때문에 평일에 조원들과 의논하여 방법을 찾아볼 예정이다.

오늘 공부한 내용

최대공약수와 최소공배수

프로그래머스의 "최대공약수와 최소공배수" 문제를 저번에 공부했던 최대공약수 구하는 유클리드 호제법을 사용해서 풀어봤다.

유클리드 호제법 정리글

코드 먼저

public class Solution {
    public int[] solution(int n, int m) {
        int[] answer = new int[2];
        
        answer[0] = GCD(m,n);
        answer[1] = (n*m) / answer[0];
        
        return answer;
    }
    
    public int GCD(int m, int n)
    {        
        if(n == 0) // 베이스 케이스
            return m;
        
        return GCD(n, m%n);
    }
}