[ RV ] 01. Probability

Axiomic definition of probability

Ex_ die experiment
U = { 1, 2, 3, 4, 5, 6 } ~ Sample space
→ 1, 2 ... 하나하나가 outcome, sample point
$\phi$, {1}, {1, 3, 5} ~ Event

Sample space : a collection of all sample points of a random experiment
Event: a subset of the sample space

Probability axioms

• P(A) $\ge$ 0
• P(u) = 1
• If AB = $\phi$, then P(A$\cup$B) = P(A) + P(B)
• Probability is assigned to event

Properties

• $P(\phi) = 0$
• $P(A\cup B) = P(A) + P(B) - P(A\cap B)$
• $P(A^c) = 1 - P(A)$
• If { A$_1$, A$_2$ ... A$_n$ } is a sequence of mutually exclusive event
  $P(\bigcup_{i=1}^n A_i) = \Sigma_{i=1}^nP(A_i)$

---

Conditional Probability

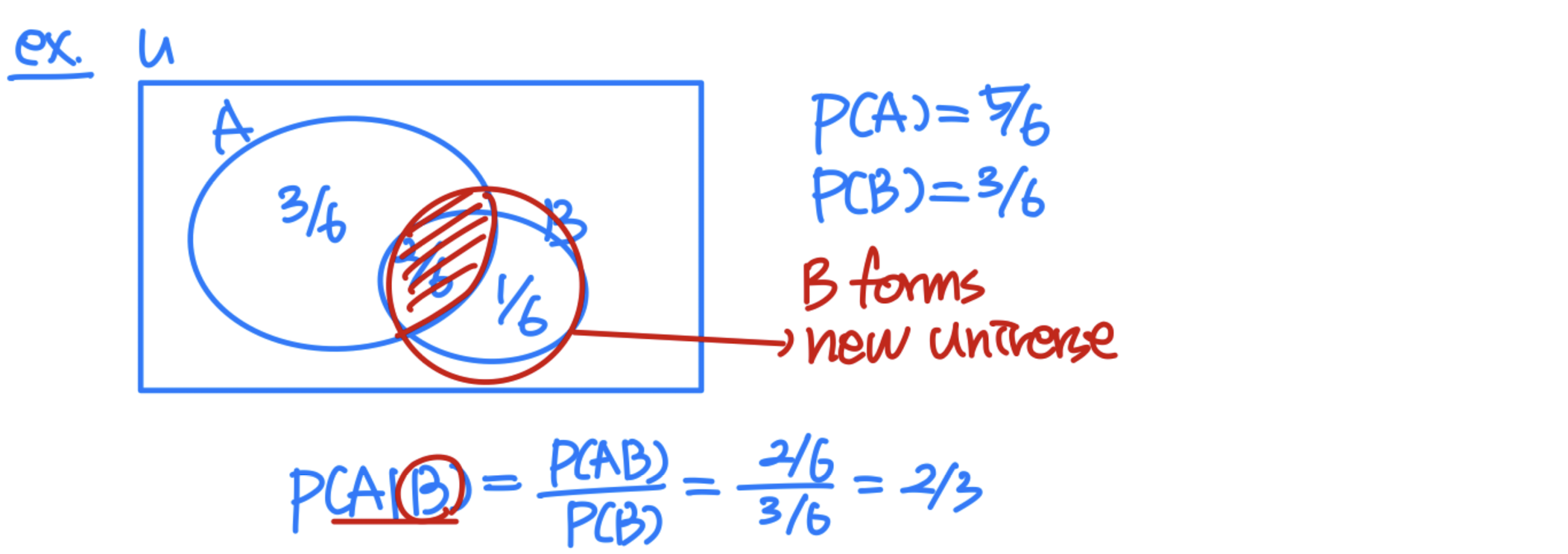
Def : The conditional probability of an event A given B is defined as
P(A|B) = $\frac{P(AB)}{P(B)}$ = P(B|A) $\frac{P(A)}{P(B)}$ → P(B) can not be 0
$\Leftrightarrow$ P(AB) = P(A|B)P(B) → P(B) can be 0, Generable

---

⭐️ Total Probability Theorem

{ $A_1, ... , A_n$ } → partition of $u$
P(B) = P(A$_1$B) + P(A$_2$B) + P(A$_3$B)
         = P(B|A$_1$)P(A$_1$) + P(B|A$_2$)P(A$_2$) + P(B|A$_3$)P(A$_3$)
         = $\Sigma^3_{i=1}$P(B|A$_i$)*P(A$_i$)

In general, P(B) = $\Sigma^n_{i=1}$P(B|A$_i$)*P(A$_i$)  Don't forget!
~ " Total Probability Theorem "

Ex_

A : Airplane is flying
B : Alarm ringsP(AB) = P(A)*P(B|A)
P(A) = 0.05
P(B|A) = 0.99 ~ "Prob. of detection"
P(B|A$^c$) = 0.10 ~ "Prob. of false alarm"
P(AB) = 0.05 * 0.99 = 0.0495

P(B) = 0.05 0.99 + 0.95 0.10 = 0.1445

P(A|B) = $\frac{P(AB)}{P(B)}$ = $\frac{0.0495}{0.1445}$ = 0.34
→ too small. why? Because P(A) = 0.05
P(A$^c$|B) = 0.66

Ex2_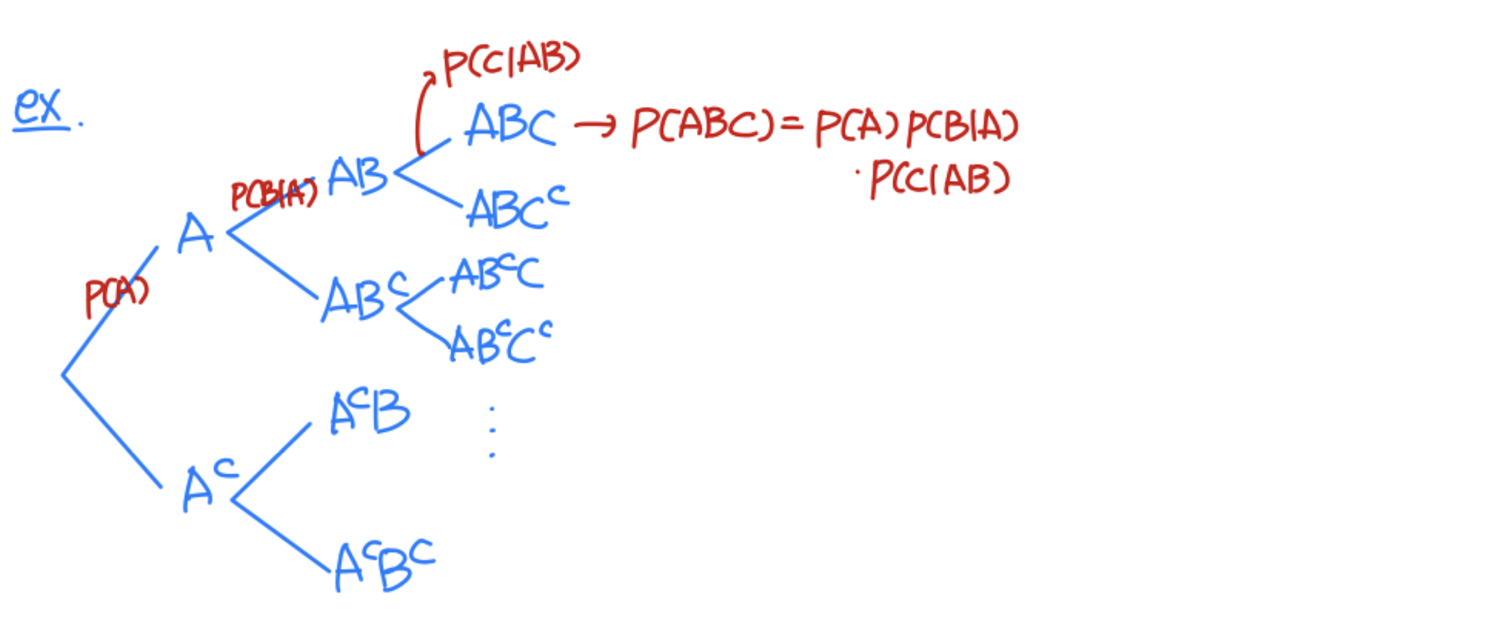

P(ABC) = P(AB) * P(C|AB)
              = P(A) * P(B|A) * P(C|AB) ~ " Chain rule " = " multiplication rule "

---

Baye's rule

$P(A_i|B)$ = ?
$P(A_i)$ ~ " prior probability " ~ initial belief

$P(A_i|B) = P(B|A_i) * \frac{P(A_i)}{P(B)}$
= $\frac{P(A_i)P(B|A_i)}{\Sigma^n_{i=1}P(B|A_i)P(A_i)}$ ~ " Baye's rule "

Ex_ Select a box and pick a component

(a) What is the probability that the picked one is defective?

P(D) = $\Sigma^4_{n=1}$P(D|B$_n$)P(B$_n$)
         = 1/4 * (0.05 + 0.4 + 0.1 + 0.1) = 0.1625

(b) If the picked one is defective, what is the probability that it came from Box 2?

P(B$_2$|D) = $\frac{P(D|B_2)P(B_2)}{P(D)}$
              = $\frac{0.4*0.25}{0.1625}$ = 0.6154

---

Independence

Definition

Two events A and B are said to be independent iff
P(A|B) = P(A) $\Leftrightarrow$ P(AB) = P(A) * P(B)

• Probability of A is not changed whether or not an occurrence of B is assumed.
  
  
• Ex_ Tossing a coin twice
  • U = { HH, HT, TH, TT }
  • H$_1$ = { First toss is head }
  • H$_2$ = { Second toss is head }
  • P(H$_1$H$_2$) = 1/4 = P(H$_1$)P(H$_2$)
    → H$_1$ and H$_2$ are independent
    
    
• Question : If P(A) ≠ 0 and P(B) ≠ 0, can these two events be both independent and mutually exclusive?
  Answer : No. totally different concept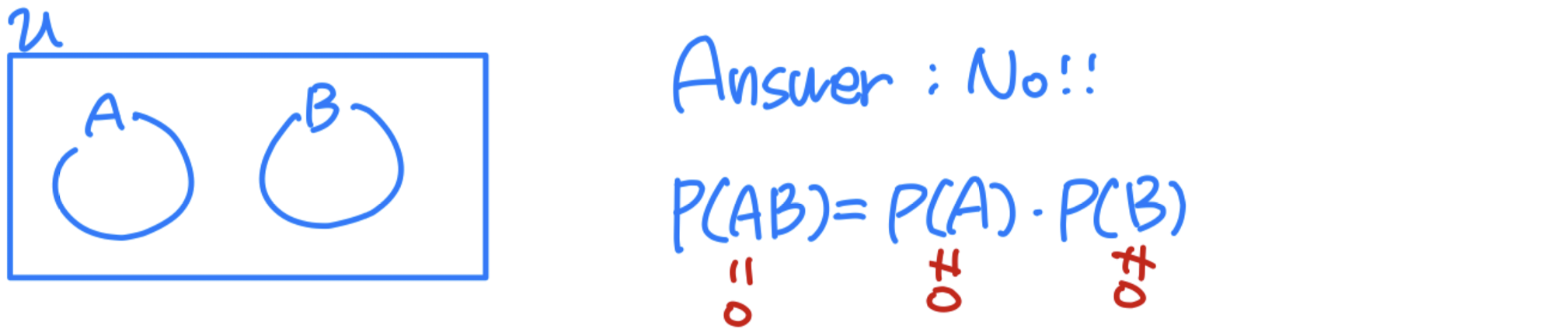

Conditional independence

P(AB|C) = P(A|C) * P(B|C)

• independence와 conditional independence는 관련 X

Ex_ Consider two unfair coins A and B

P(head|A) = 0.9 and P(head|B) = 0.1
choose a coin and toss it twice
H$_1$ = { First toss is head } and H$_2$ = { Second toss is head }

(a) Once we know it is coin A, are H$_1$ and H$_2$ independent?
P(H$_1$H$_2$|A) = P(H$_1$|A) * P(H$_2$|A)
   0.9 * 0.9 = 0.9 * 0.9
→ H$_1$ and H$_2$ are conditionally independent

(b) If we don’t know which coin it is, are H$_1$ and H$_2$ independent?
P(H$_1$H$_2$) = P(H$_1$) * P(H$_2$)

P(H$_1$) = P(H$_1$A)P(A) + P(H$_1$B)P(B)
           = 1/2 * (0.9 + 0.1) = 1/2
P(H$_2$) = 1/2
P(H$_1$H$_2$) = P(H$_1$H$_2$|A)P(A) + P(H$_1$H$_2$|B)P(B)
                = 0.9 * 0.9 * 0.5 + 0.1 * 0.1 * 0.5 = 0.41 ≠ P(H$_1$)P(H$_2$)
→ H$_1$ and H$_2$ are dependent

Independence of collection of events

Events A$_1$, A$_2$, ... , A$_n$ are said to be independent iff
$P(\bigcap_{i \in I}A_i$) = $\Pi_{i \in I}P(A_i)$, for any set of distinct indexes $I \subset$ { 1, 2, ... , n }

Pairwise independence

Events A$_1$, A$_2$, ... , A$_n$ are said to be pairwise independent iff
P(A$_i$A$_j$) = P(A$_i$)P(A$_j$), $\forall_{i≠j}$

Ex_ Consider two independent fair coin tosses
A = { first toss is head } = { HH, HT } → P(A) = 1/2
B = { second toss is head } = { HH, TH } → P(B) = 1/2
C = { first and second toss give the same result } = { HH, TT } = 1/2

P(AB) = 1/4, P(BC) = 1/4, P(CA) = 1/4
→ A, B, and C are pairwise independent

Pairwise independence does not imply independence.

⭐️ Ex_

Trains X and Y arrive at a station at random and independently between 8:00 AM and 8:20 AM. Train X stops for 4 minutes and train Y stops for 5 minutes.
A = { X arrives (t1, t2) } → P(A) = $\frac{t_2-t_1}{20}$
B = { Y arrives (t3, t4) } → P(B) = $\frac{t_4-t_3}{20}$
P(AB) = P(A)P(B) = $\frac{(t_2-t_1)(t_4-t_3)}{400}$

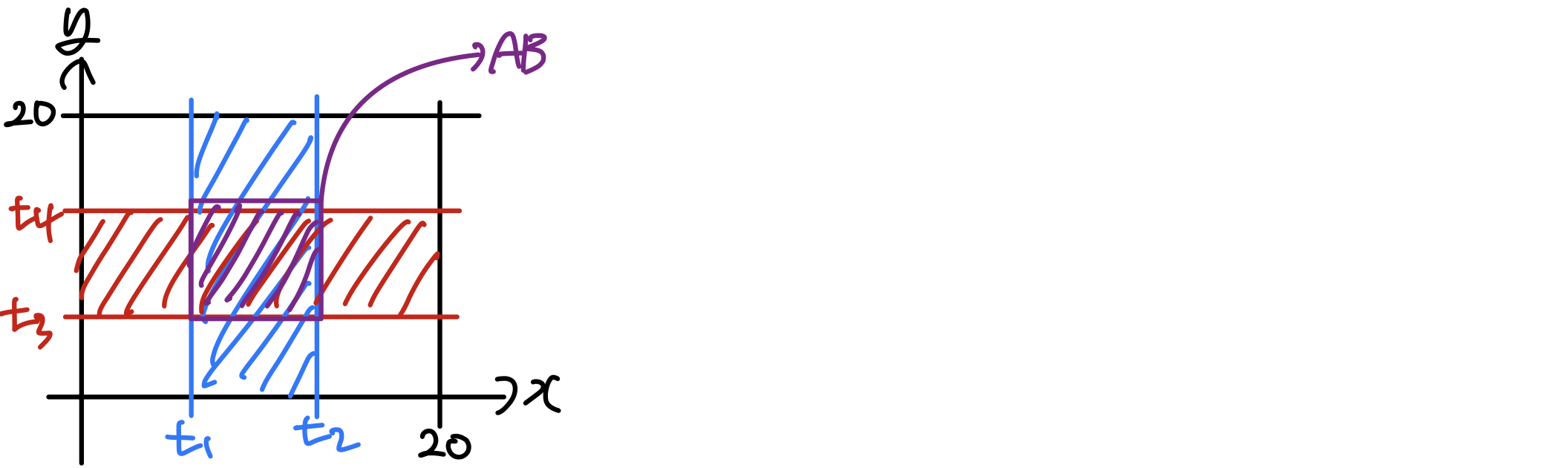
(a) What is the probability that X arrives earlier than Y?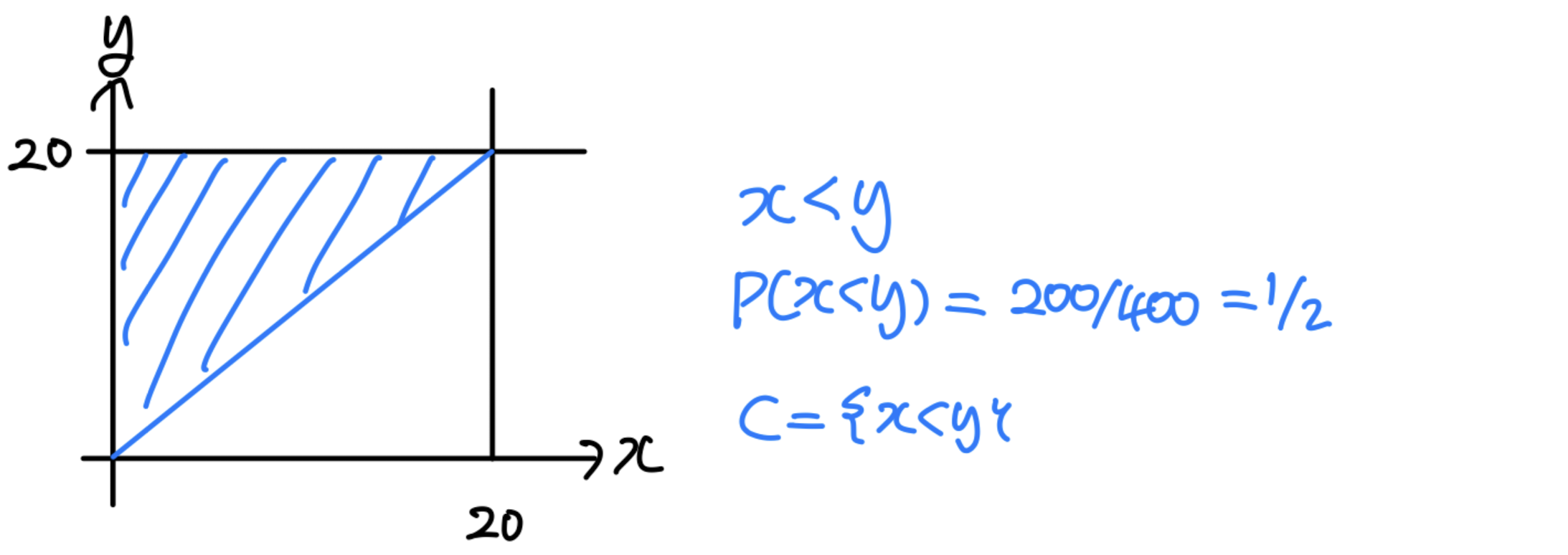

(b) What is the probability that X meets Y?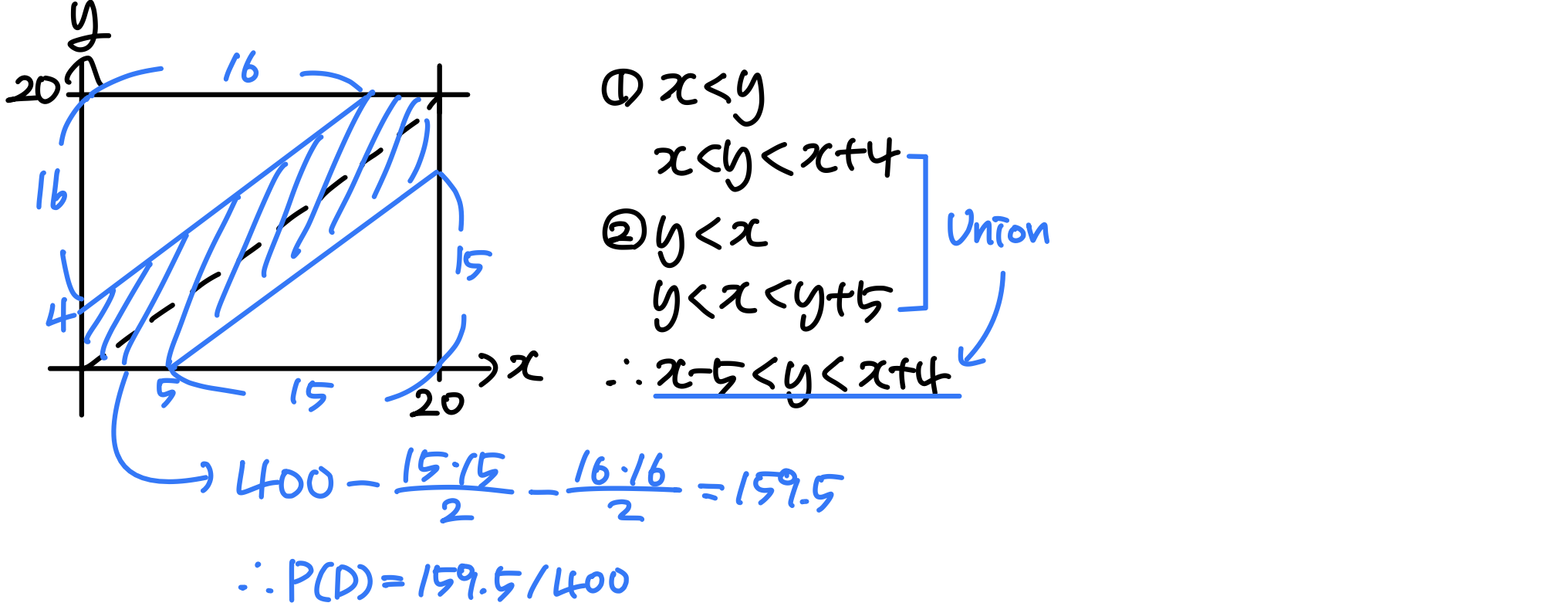

(c) What is the probability that X arrives earlier than Y assuming that they meet?

---

Computation of probability by counting

Ex_ We will toss 2 dice. What is the probability of getting a sum of 7?
P(A) = 6 / 36

We calculated this probability simply by counting the number of outcomes because all outcomes are equally-likely ( uniform )
→ prob. of outcomes all the same

Counting principle

• experiment consisting of $r$ stages
• $\exists$ n$_i$ choices at stage $i$
• number of choices = n$_1$ x n$_2$ x ... x n$_r$

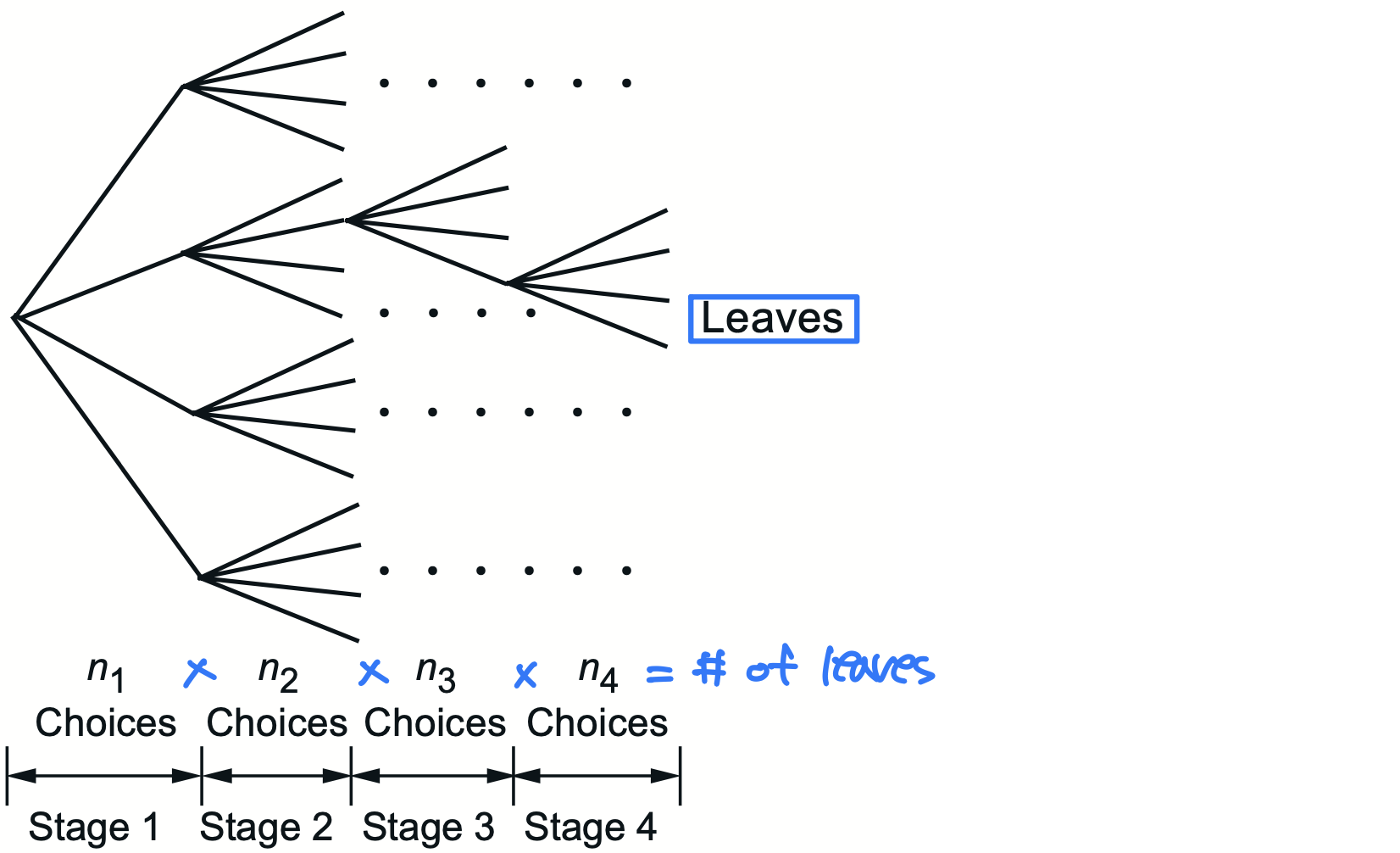
Ex number of license plates (e.g. HGU0387)
→ 26 × 26 × 26 x 10 x 10 x 10 x 10
Ex number of license plates if repetition is not allowed
→ 26 x 25 x 24 x 10 x 9 x 8 x 7
Ex_ number of subsets of an n-element set
→ 2$^n$ $\Rightarrow$ 2(choice or not) x 2 x ... x 2 ( n개 )

Permunations

What is number of ways of ordering n elements?
→ n!

k-permutations: number of ways of picking k out of n objects and arrange them in a sequence
→ $_n$P$_k$ = $\frac{n!}{(n-k)!}$

Ex_ number of words that consist of four distinct letters
$_2$$_6$P$_4$ = 26 x 25 x 24 x 23

Conbinations

number of k-element subsets of a given n-element set
no ordering of the selected elements
Ex_ number of forming a committee of k people out of n

($^n_k$) = $_n$C$_k$ " $n$ choose $k$ "
      = $\frac{n!}{(n-k)!k!}$

" binomial coefficients "
Ex_ $\Sigma_{k=0}^n(^n_k)$ = 2$^n$

⭐️ Partitions

$(^n_k)$ - same as partitioning the set in two

Ex_ 52 card deck, dealt to 4 players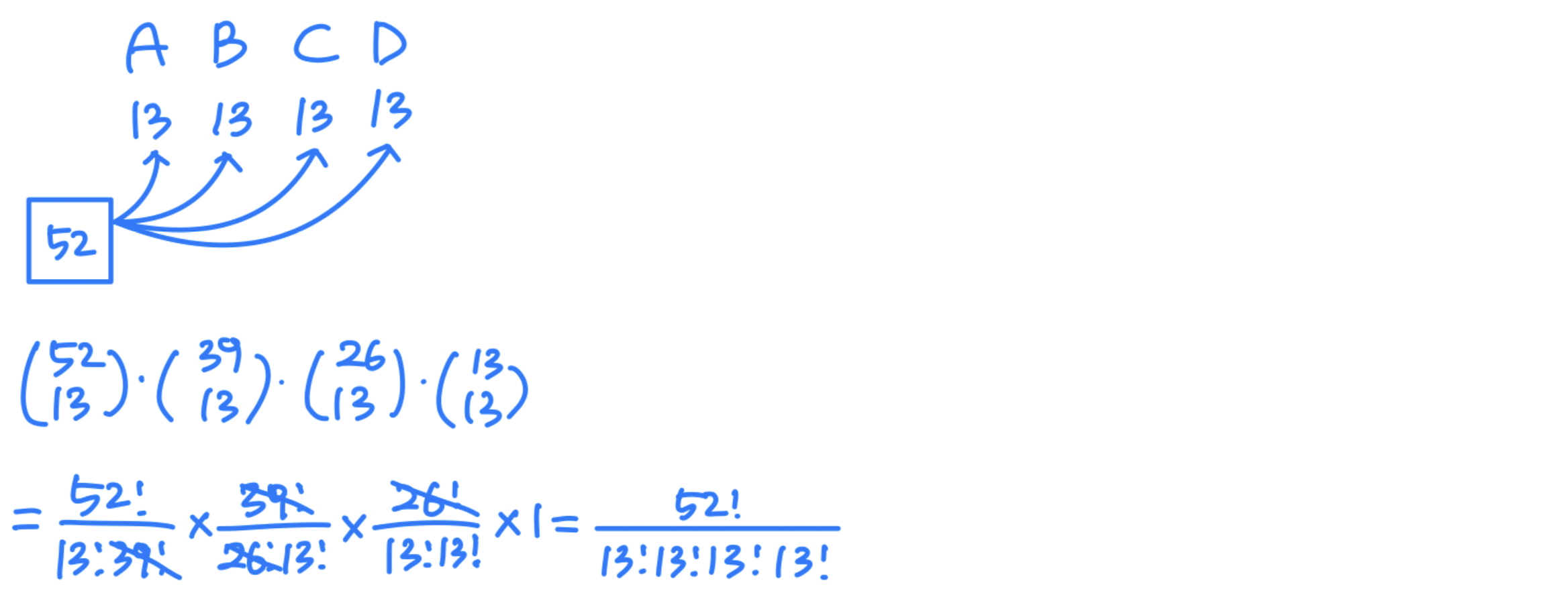

n number of partitioning n elements in $r$ groups, with the $i$th group containing $n_i$ elements, $\Sigma^r_{i=1} n_i = n$
→ $\frac{n!}{n_1!*n_2!...n_r!}$

Bernoulli trials

Ex_ We toss 5 coins independently.
P(H) = p
P(HHHTT) = $p$ * $p$ * $p$ * $(1-p)$ * $(1-p)$ = $p^3(1-p) ^2$
P (3 heads and 2 tails in any order) =?
→ $(^5_3)$ * $P^3$ * $(1-p)^2$

Let A be an event in a random experiment with P(A) = $p$ and P(A$^c$) = 1-$p$.
Repeating this experiment $n$ times, probability that $A$ occurs $k$ times in any order is calculated by
$P_n(k) = (^n_k)p^k(1-p)^{n-k}$ ~ " binomial probability "

Ex_ Consider a die experiment.
A = {$f_1$}.
P(A) = $p$ = 1/6.
P$_5$(2) = ?
→ $(^5_2)$ * $(\frac{1}{6})^2$ * $(\frac{5}{6})^3$

Ex_ Suppose a 4-faced die is tossed 12 times. Find the probability that 1 is twice, 2 is three times, 3 is three times, and 4 is four times.
→ 1 1 2 2 2 3 3 3 4 4 4 4 → $(\frac{1}{4})^{12}$
→ $\frac{12!}{2!3!3!4!}$ * $(\frac{1}{4})^{12}$

⭐️ Generalization
Let [A$_1$,A$_2$,··· ,A$_r$] be a partition of $U$. Let P(A$_i$) = $p_i$, $\Sigma_{i=1}^rp_i$ = 1, and $\Sigma_{i=1}^rk_i$ = n.
Then, P$_n(k_1, k_2, ... , k_r)$ = $\frac{n!}{k_1!k_2!k_3!...k_r!}p_1k_1p_2k_2...p_rk_r$

HGU 전산전자공학부 이준용 교수님의 23-2 확률변수론 수업을 듣고 작성한 포스트이며, 첨부한 모든 사진은 교수님 수업 PPT의 사진 원본에 필기를 한 수정본입니다.