[ Statistics ] 04. Probability and Counting Rules

1. Sample Spaces and Probability

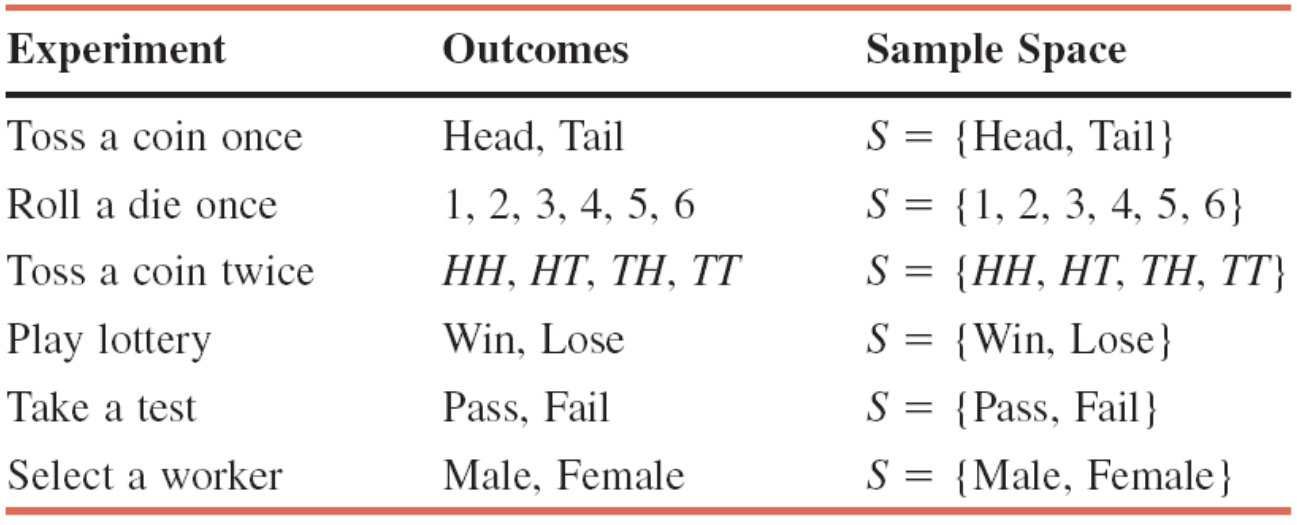
Classical probability

Empirical probability

Subjective probability

주관적인 판단, 경험, 정보 및 믿음을 바탕으로 사건에 할당된 확률
확률을 할당하는 명확한 규칙은 없다.

---

2. Mutually exclusive

3. The Multiplication Rules and Conditional Probability

Independent (독립) vs. Dependent (종속)

→ van diagram으로 표현 못함

Conditional probability

---

4. Counting Rules

• 기본적인 Counting rule
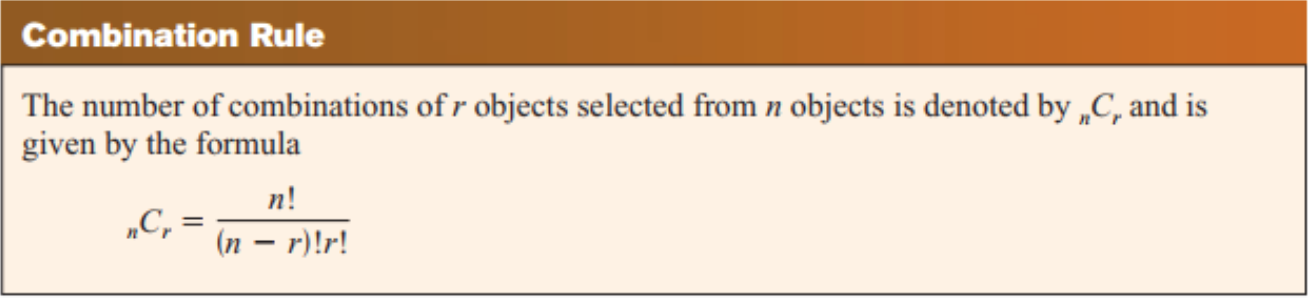
• Combinations

---

Ex_

---

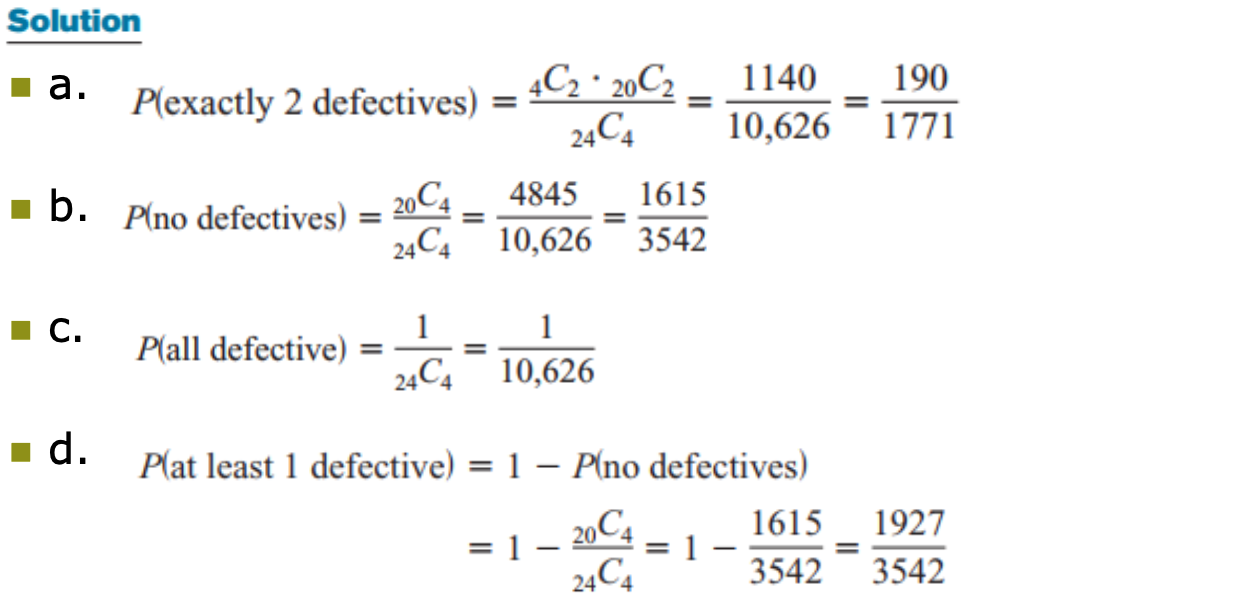
Bayes Theorem

• 𝑘개의 사상(event) $B_1$ ,$B_2$ ,⋯,$B_k$가 서로 배반사상(mutually exclusive event)이면
  𝑃(𝐵$_1$∪𝐵$_2$∪⋯∪𝐵$_k$) = 𝑃(𝐵$_1$)+𝑃(𝐵$_2$)+⋯𝑃(𝐵$_k$)
                                = $\bigcup^k_{i=1}B_i$
• 표본공간 𝑆를 𝑘개의 서로 배반인 사상 $B_1$ ,$B_2$ ,⋯,$B_k$로 나누면,
  임의의 사상 𝐴는 𝑘개의 서로 배반인 사상$A = (A\cap B_1)\cup(A\cap B_2)\cup ... \cup(A\cap B_k)$ 로 나누어진다.
  따라서 $P(A) = P(A\cap B_1)+P(A\cap B_2)+...+P(A\cap B_k)$
             $P(A) = P(B_1)P(A|B_1)+P(B_2)P(A|B_2)+...+P(B_k)P(A|B_k)$

전확률공식 (total probability law)

표본공간 𝑆를 𝑘개의 서로 배반인 사상 $B_1$ ,$B_2$ ,⋯,$B_k$로 나누면, 임의의 사상 A에 대해
$P(A) = \sum^k_{i=1} P(B_i)P(A|B_i)$›

⭐️ 베이즈 정리 (Bayes Theorem)

표본공간 𝑆를 𝑘개의 서로 배반인 사상 $B_1$ ,$B_2$ ,⋯,$B_k$로 나누고, P(A) > 0 이면,
$P(B_i|A) = \frac{P(B_i)P(A|B_i)}{\sum^k_{j=1}P(B_j)P(A|B_j)} ,i = 1, 2, ... , k$
→ $P(B_i)$ : 사전확률 (prior prob.)
→ $P(B_i|A)$ : 사후확률 (posterior prob.)

• 예제 : 결핵감염여부 조사를 위한 투베르클린 반응검사에서
  • 임상실험결과 감염율 10%, 비감염율 90%
  • 감염자 중 양성반응 95%
  • 비감영자 중 양성반응 10%
  • 양성반응자 중에서 실제로 감염되었을 확률은?
• 예제2 : A telephone hotline service
  • $A_1$ - application sw 48% → 0.90 resolved
  • $A_2$ - hardware 38% → 0.15 resolved
  • $A_3$ - inability to install 14% → 0.80 resolved
  • Resolved call이 hardware이었을 확률은?

HGU GLS학부 김헌주 교수님의 23-2 통계학 수업을 듣고 작성한 포스트이며, 첨부한 모든 사진은 교수님 수업 PPT의 사진 원본에 필기를 한 수정본입니다.