[ Algorithm ] 01. Getting Started

Insertion sort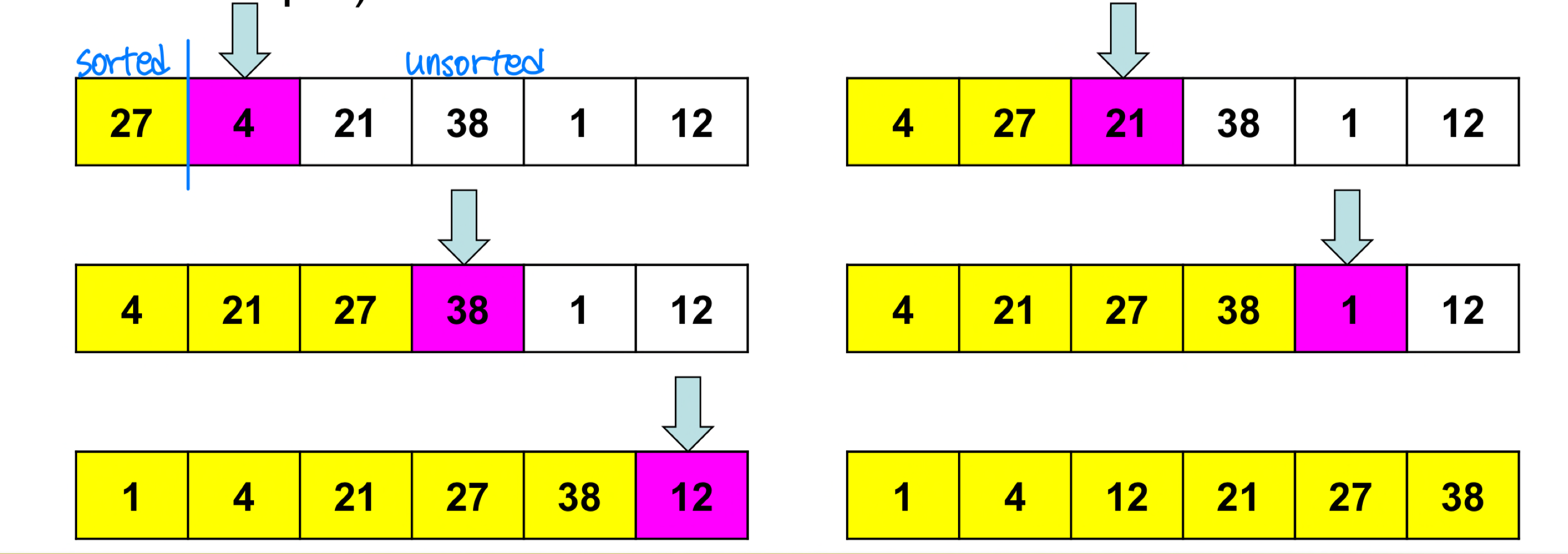

Design paradigms

• Insertion-sort uses incremental approach : subarray A[1 ... j-1], insert A[j]
  c.f) D and C approach ( merge sort )

Analysis

• Correctness : Proving the correctness of the algorithm
• Efficiency : Obtaining the time complexity of the algorithm

Correctness using Loop invariants

• similar to mathematical induction
• Loop invariant(불변) : At the start of each iteration of the for loop, the subarray A[1..j-1] consists of the elements originally in A[1..j-1] but in sorted order ➡️ elements가 변하지 않음
• Initialization : when j=2, A[1..j-1] consists of the single element A[1]. Trivially sorted
• Maintenance(유지) : Informally, the body of outer ‘for’ loop works by moving A[j-1], A[j-2], A[j-3], and so on, by one position to the right until the proper(적절한) position for A[j] is found
• Termination : The outer ‘for’ loop ends when j = n+1. Thus, A[1..n] consists of the elements originally in A[1..n] but in sorted order

Efficiency

• Predicting the resources – time, storage(not a big deal)
• Random-access machine (RAM) model ( a generic one ) 일반적인 모델
  • Instructions are executed one after another ( no concurrent operations)
  • Each instruction takes a constant time
    - Arithmetic, Data movement, Control
  • Data types : integers, floating point
  • No memory hierarchy ( no cache or virtual memory )
    
    
• Input size
  - n numbers
  - Graph algorithms : # of vertices and edges
  
  
• Running time
  - The # of primitive(기본적인) operations or “steps” executed.
  - Steps are defined to be machine-independent
  - Each line of pseudocode requires a constant time
  but take different time
  
  
• Time complexity Analysis
  - Worst-case (usually) : upper bound
  - Average-case (sometimes) : Need assumption of statistical distribution(통계적 분포) of inputs
  - Best-case (bogus) : 의미 없음, cheat

Analysis of insertion-sort

Analysis of merge-sort

use a recurrence equation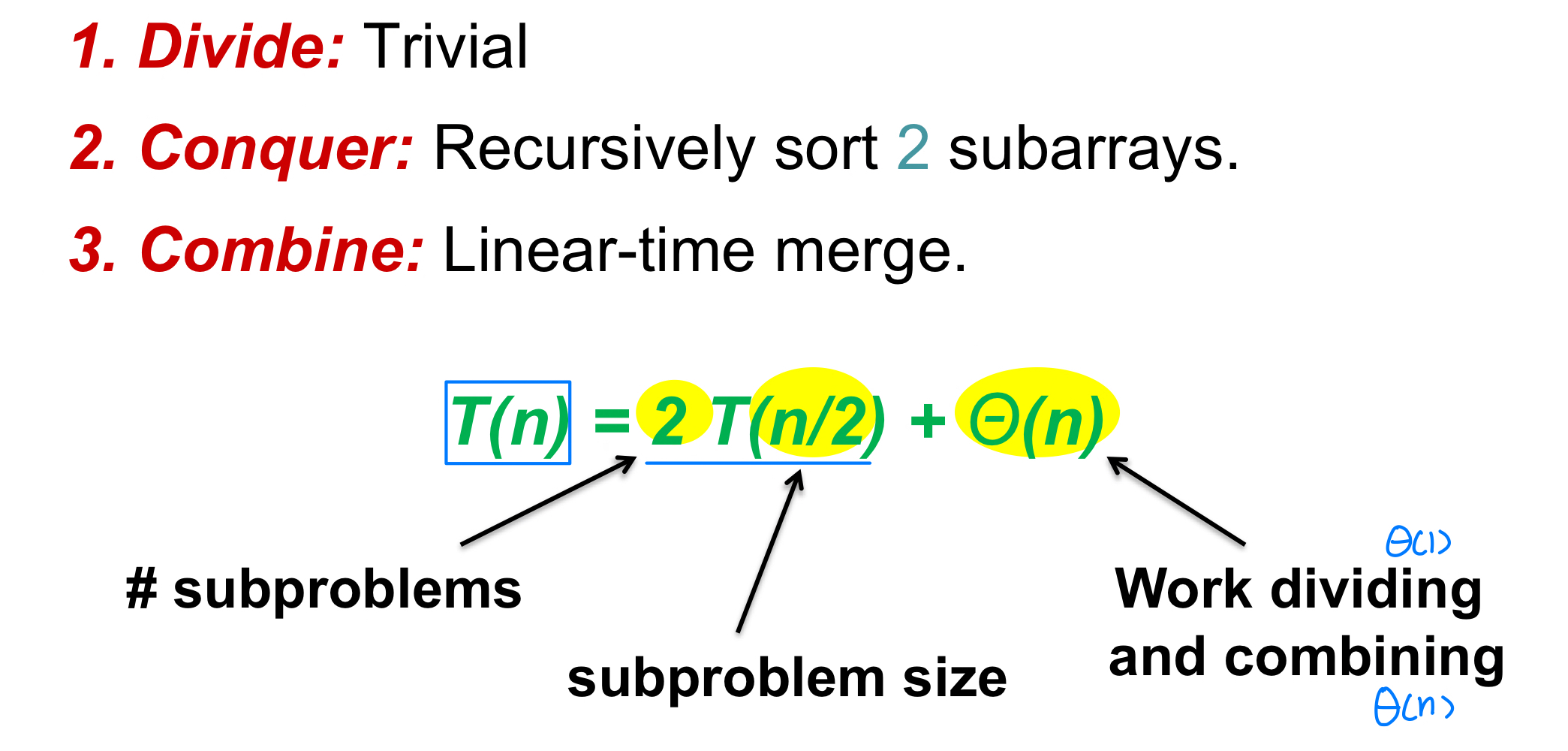

• By the master theorem, T(n) = Θ(n lg n)
• Compared to insertion sort Θ($n^2$)
• On small inputs, insertion sort may be faster
  But, for large enough inputs, merge sort will always be faster

using recursion tree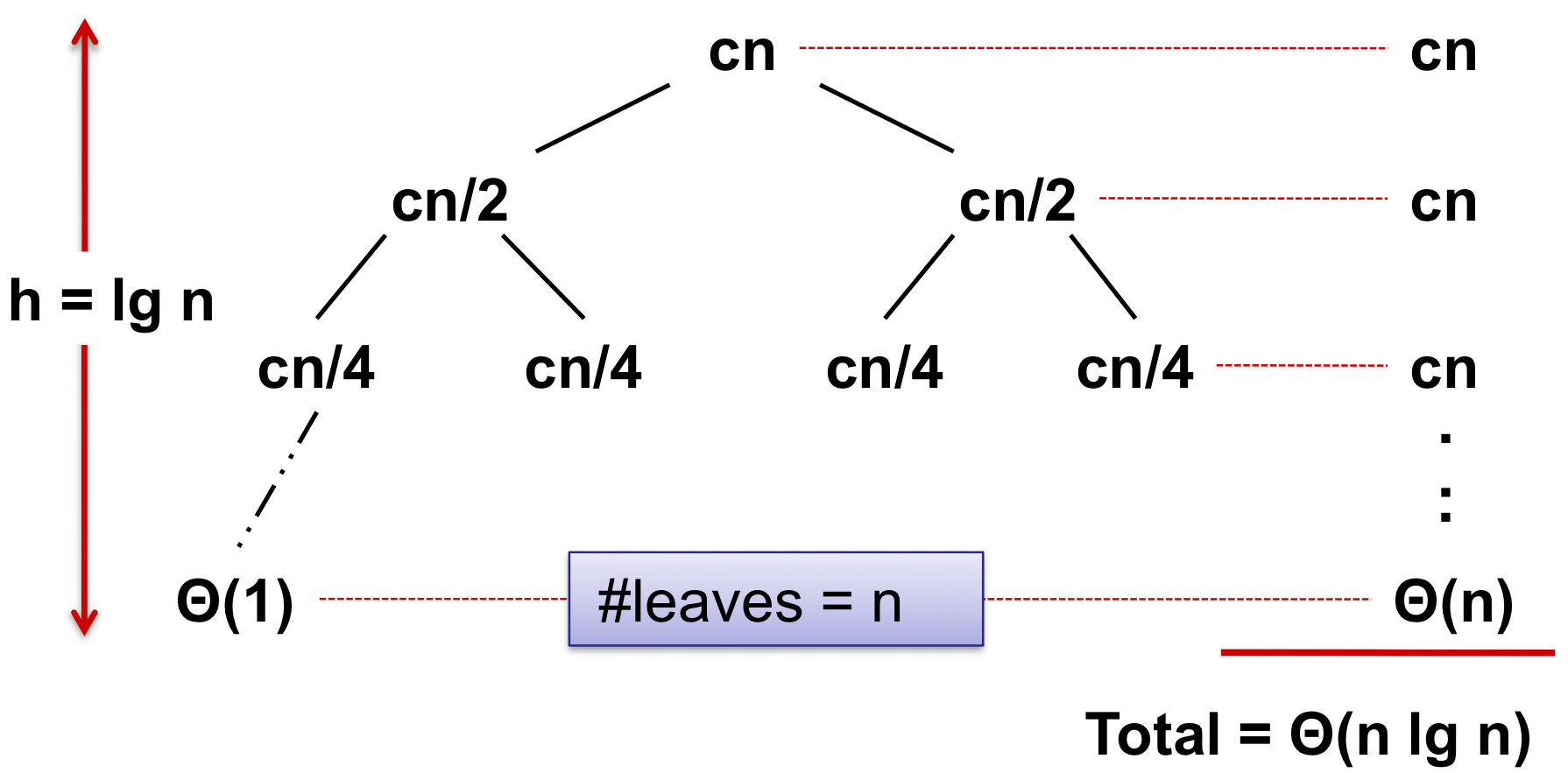

Exercise

1. Space complexity of fibo(n) (memoized DP)

➡️ $\Theta$(n)
why? array size = $\Theta$(n) AND stack(function call) : 최대 n번까지 call ($\Theta$(n))

2. Another sort

Selection sort

$T(n) = T(n-1) + \Theta(n)$
$\Theta(n^2)$ Best, Worst case 동일

Bubble sort

$T(n) = T(n-1) + Θ(n)$
Time complexity : $\Theta(n^2)$ Best, Worst case 동일

Insertion sort

recurrence equation : $T(n) = T(n-1) + O(n)$
Best : $\Theta(n)$, Worst : $\Theta(n^2)$

Quick sort

( partition : 리스트를 분할하고 pivot을 정하는 과정 )
Worst case
$T(n) = T(n-1) + T(0) + \Theta(n) = T(n-1) + \Theta(n)$
➡️ $\Theta(n^2)$
Best case (partition : pivot을 중앙값으로 선택)
$T(n) = 2T(n/2) + \Theta(n)$
➡️ $\Theta(nlgn)$

3. Binary Search

Time complexity : $\Theta(lgn)$
Insertion sort에서 검색을 이진검색으로 한다면, $\Theta(nlgn)$?
➡️ No, 찾는 건 빠르지만 이후 복사해서 옮기는 작업을 할 수 없다.

HGU 전산전자공학부 용환기 교수님의 23-1 알고리듬 분석 수업을 듣고 작성한 포스트이며, 첨부한 모든 사진은 교수님 수업 PPT의 사진 원본에 필기를 한 수정본입니다.