[ Algorithm ] 02. Growth of Functions

• The order(n, $n^2$, lgn ...) of growth of the running time of an algorithm gives a simple characterization of the algorithm's efficiency,
  and also allows us to compare the relative performance of algorithms
  - input size n ➡️ infinite, full grown 일 때 faster?
• Asymptotic efficiency - how the running time increases with the size of the input in the limit
• Focus on what’s important by abstracting away low-order terms and constant factors

Notations

O-notation : upper bound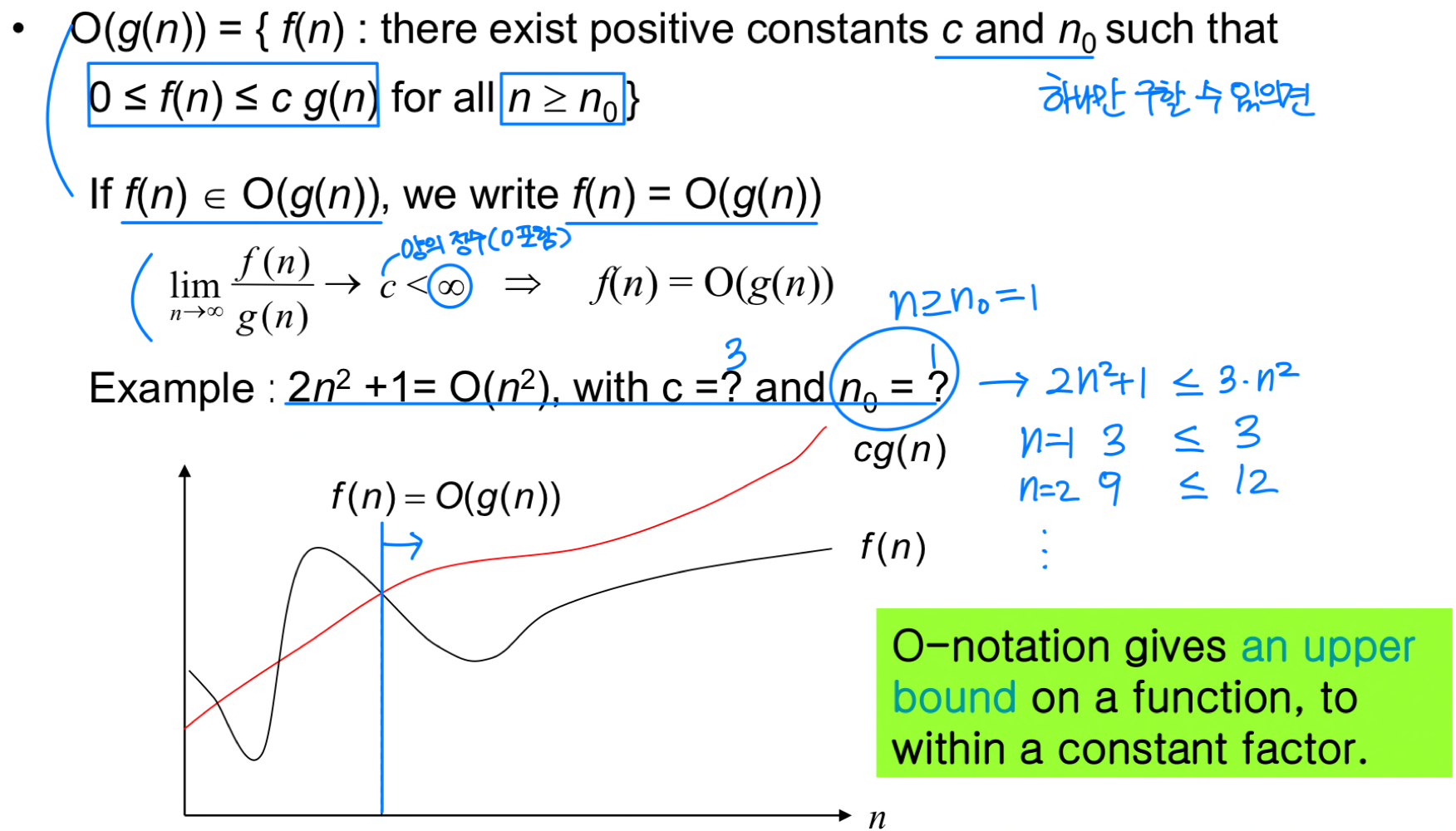

$\Omega$-notation : lower bound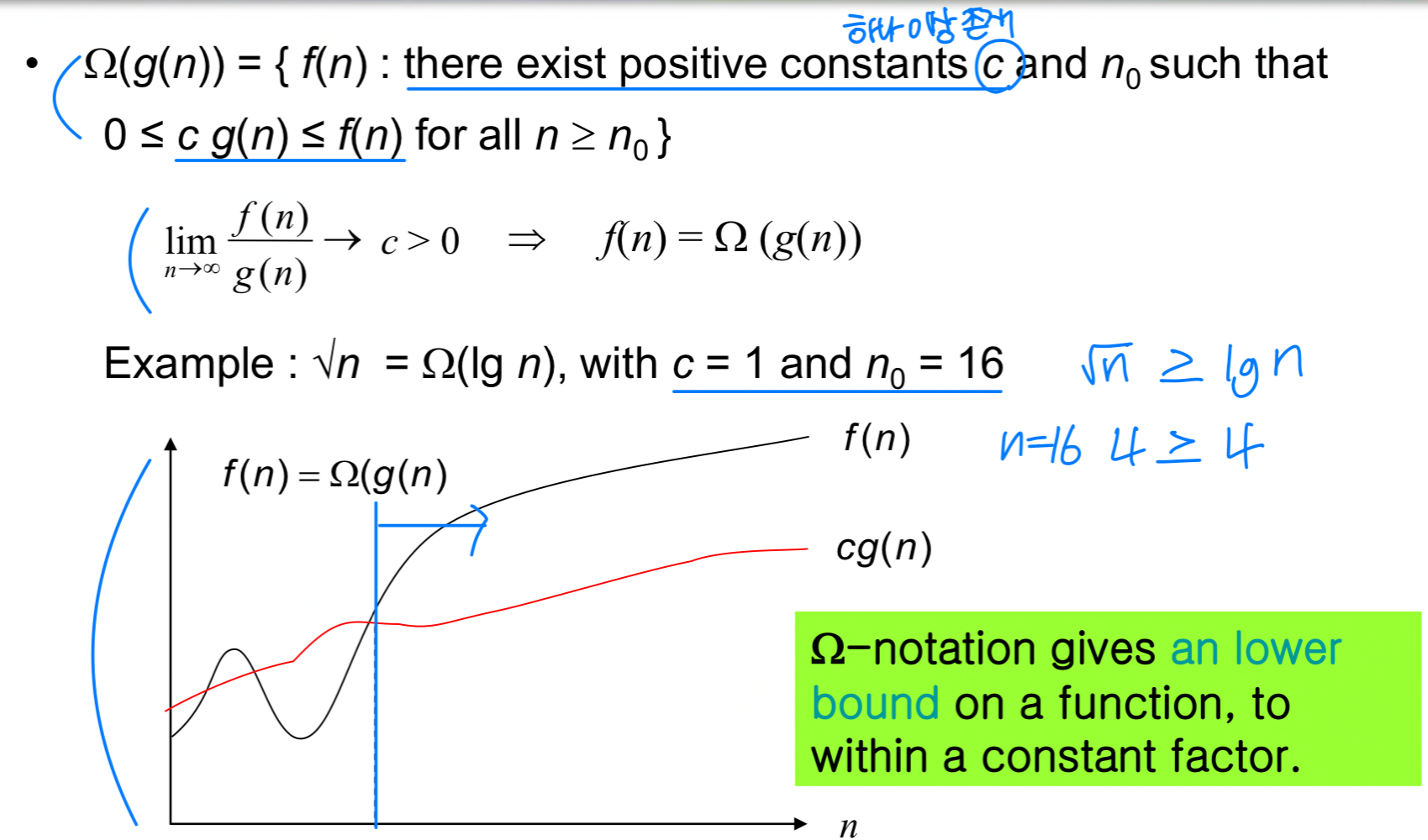

$\Theta$-notation : tight (exact) bound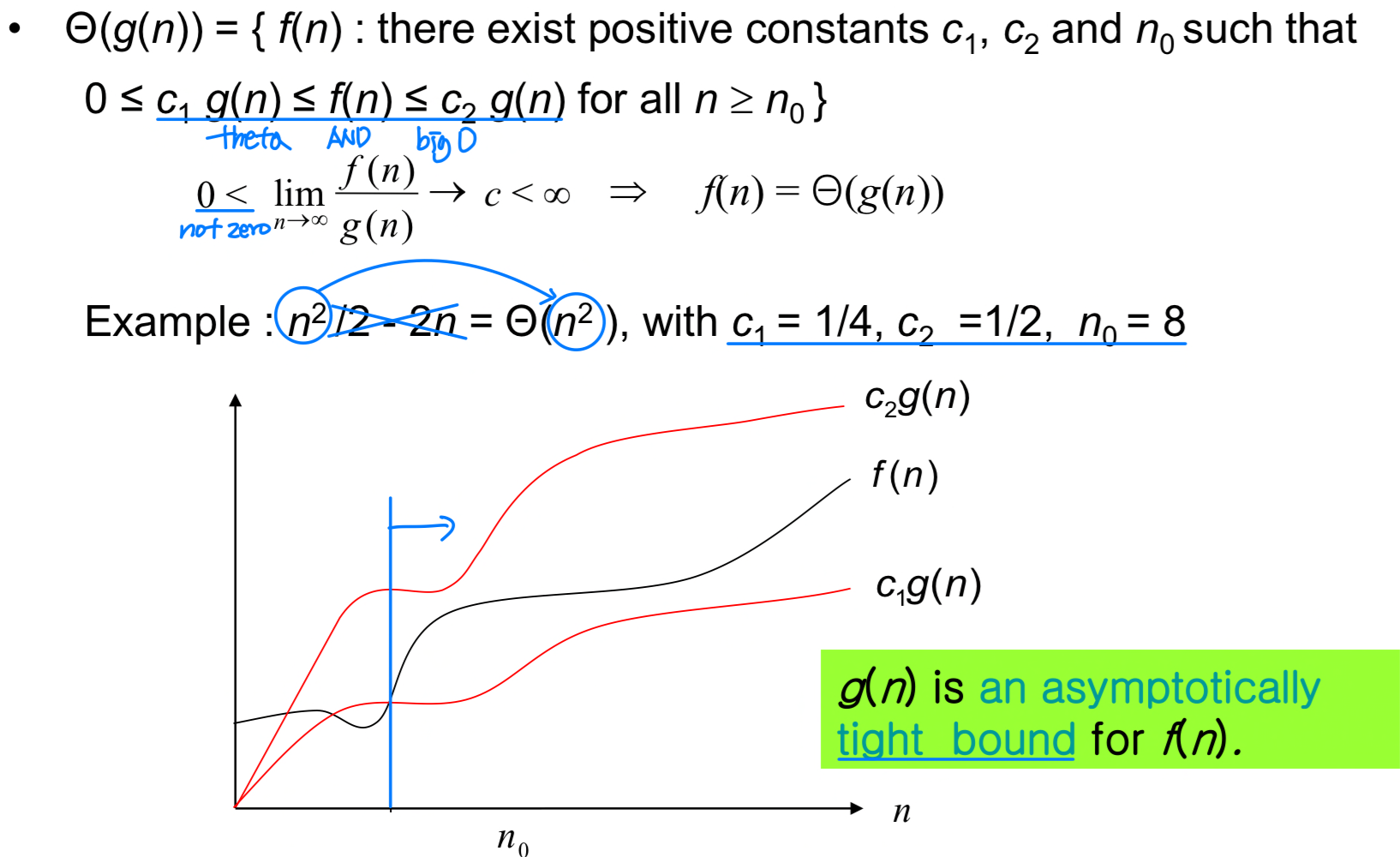

Teorem and Rule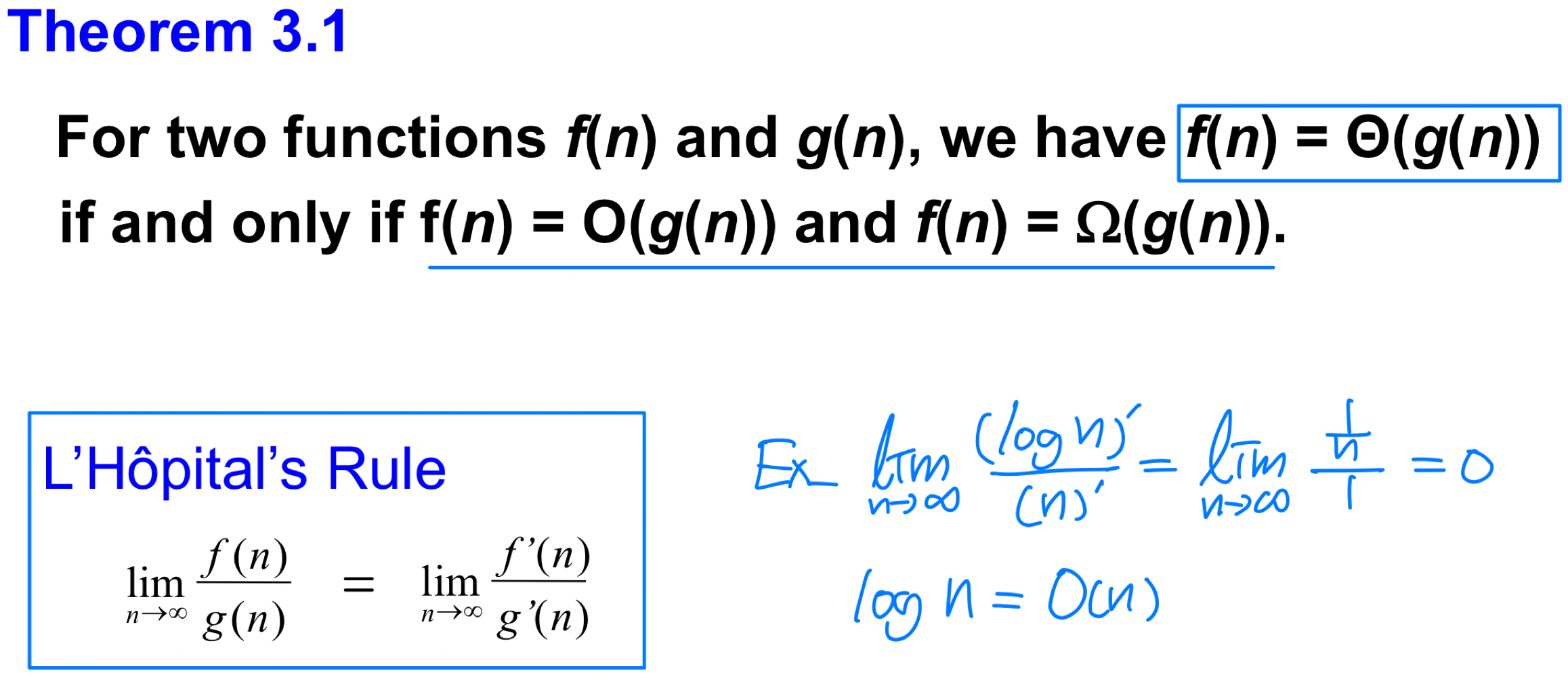

o-notation

$\omega$-notation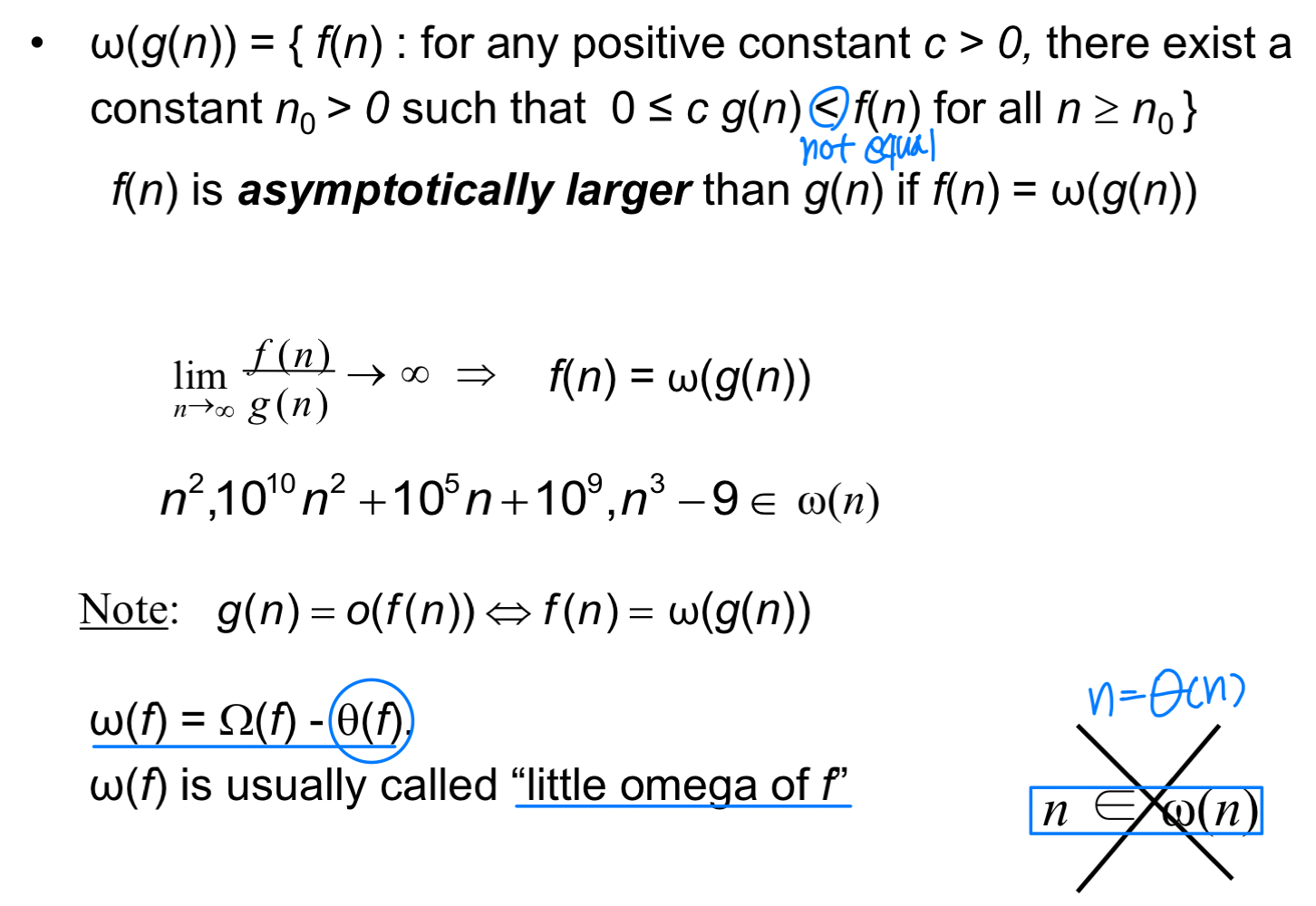

Example

➡️ Time complexity 문제 시 notation 적기!

Proposition

⭐️ Optimality of algorithm

• Each problem has inherent(내제된) complexity; that is some minimum amount of work required to solve it.
• Lower bound of problem : minimal number of operation needed to solve the problem
• When the worst-case time complexity of an algorithm matches lower bound of the problem, the algorithm is said to be optimal
• “Optimal” does not mean “the best known”; it algorithm means “the best possible”

Example

Asymptotic performance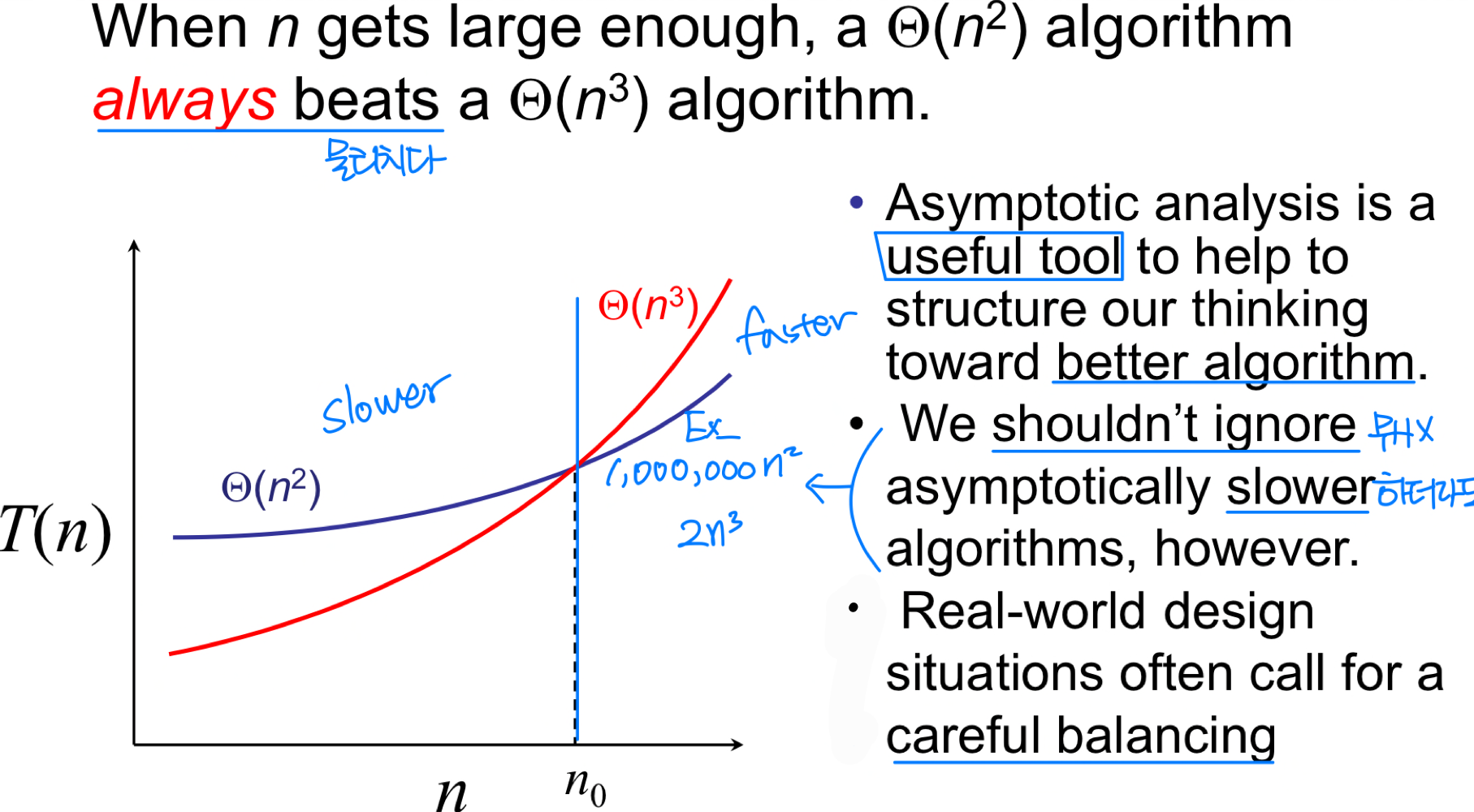

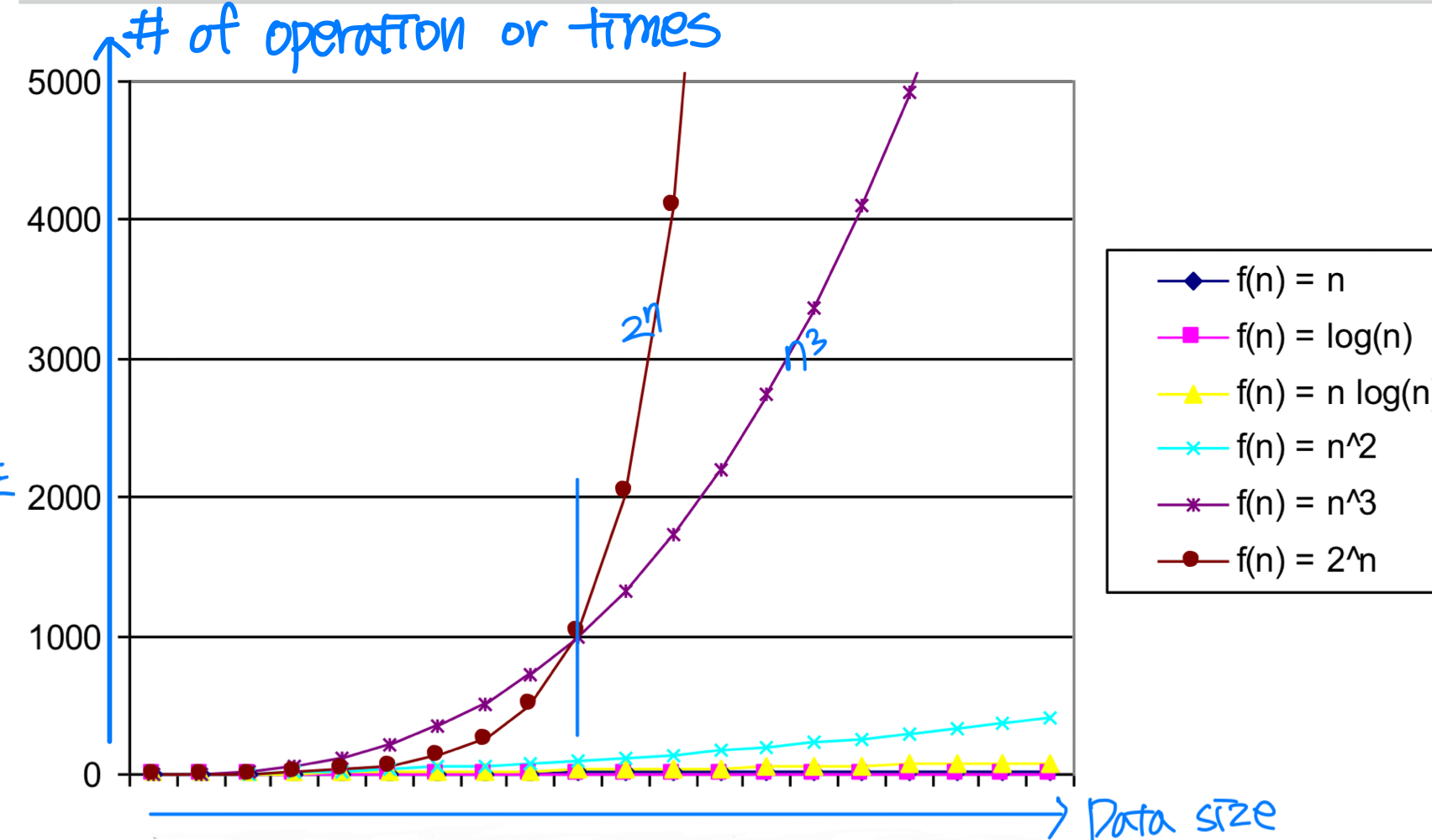
Hierarchy of Orders

Exercise in class

1. Big-Oh notation

O($g(n)$) = { $f(n)$ : for any positive constant c, there exists a constant n$_0$ > 0 such that 0 ≤ $f(n)$ ≤ c · $g(n)$ for all n ≥ n$_0$ }
For 5$n^2$ = O($n^3$), find the value of n$_0$ and c which satisfy the condition
➡️ (n$_0$, c): (1, 5), (5, 1)

2. T / F

1) 5$n^2$ = O($n^3$) : T
2) $f(n) = O(g(n))$ and $O(g(n)) = f(n)$ have same meaning : F
➡️ why? $n^2$ = O($n^3$) $\neq$ $n^3$ = O($n^2$)
3) $n^2$ + O(n) = O($n^2$) : T
4) 1/2$n^2$ = $\Theta$($n^2$) : T
5) 1/2$n^2$ = o($n^2$) : F
⭐️ 6) $f(n) + g(n) = \Theta(min(f(n), g(n))$ : F
⭐️ 7) $f(n) = O(g(n))$ implies $lg(f(n)) = O(lg(g(n)))$ : T
⭐️ 8) $f(n) = O(g(n))$ implies $2^{f(n)} = O(2^{g(n)})$ : F
➡️ why? $2n = O(n)$, but $2^{2n} \neq O(2^n)$
⭐️ 9) $f(n) = O((f(n))^2)$ : F
➡️ why? $f(n) = 1/n$, but $f(n)^2 = 1/n^2$
10) $f(n) = O(g(n))$ implies $g(n) = \Omega(f(n))$ : T
⭐️ 11) $f(n) = \Theta(f(n/2))$ : F
➡️ why? $f(n) = 2^{2n} \neq \Theta(2^n)$
12) $f(n) + o(f(n)) = \Theta(f(n))$ : T

3. Asymptotic relationship

Select all that apply.
1) lgn = O(log$_8$n)
2) lgn = $\Omega$(log$_8$n)
3) lgn = $\Theta$(log$_8$n)
➡️ All true

4. Is $2^{2n} = O(2^n)$?

No, $2^n ·2^n = 2^{2n} ≤ c2^n$를 만족하는 $n_0$ 과 $c$가 존재하지 않음

HGU 전산전자공학부 용환기 교수님의 23-1 알고리듬 분석 수업을 듣고 작성한 포스트이며, 첨부한 모든 사진은 교수님 수업 PPT의 사진 원본에 필기를 한 수정본입니다.