Asymmetric Key Encipherment - ECC(Elliptic Curve Cryptography)

Asymmetric Key Encipherment의 대표적인 암호화 기법 중 하나인 ECC(Elliptric Curve Cryptography)에 대한 포스팅을 할 것이다.

Elliptric Curve를 이용한 암호화 기법 중 대표적인 기법은 Elgamal 암호 시스템이 있다.

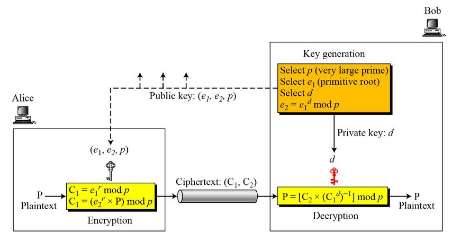
Elgamal 암호 시스템

Key Generation

1. $E_{p}(a, b)$를 선택한다.
   타원 곡선 함수 방정식 $y^{2} = (x^{3} + ax + b) \mod p$에서 $p$, $a$, $b$를 선택한다는 뜻 이다.

2. 타원 곡선에서 임의의 좌표 $e_{1}$을 선택한다.
   $e_{1} = (x_{1}, y_{1})$

3. 개인키 d를 선택한다.

4. 공개키가 되는 $e_{2} = (x_{2}, y_{2})$를 계산한다.
   $e_{2} = d * e_{1}$

5. 공개키: $e_{1}$, $e_{2}$, $E_{p}$
   개인키: d

Encryption

1. Plain Text인 $P$는 타원 곡선의 좌표가 된다.
   $r$은 salt로 임의의 수 이다.

2. Cipher Text는 $C_{1}$, $C_{2}$로 2개이다.
   $C_{1} = r * e_{1}$
   $C_{2} = P + r * e_{2}$

Decryption

1. 개인키($d$)를 이용하여 decryption 한다.
   $P = C_{2} - (d * C_{1})$

Decryption 방정식 증명

$P = C_{2} - (d * C_{1})$
$= P + r * e_{2} - (d * r * e_{1})$
$= P + (r * d * e_{1}) - (r * d * e_{1})$
$= P + 0$
$= P$

Elgamal 암호화의 문제점

평문($P$)이 타원 곡선의 점(좌표)가 되어야 한다.

따라서 타원 곡선의 점과 plain text를 mapping 하기 어렵다는 한계가 존재한다.