타원 곡선 암호(ECC: Elliptic Curve Cryptography)

RSA의 public key인 n의 크기는 보안 측면에서 1024bits 이상이 권장되고 있다.

이는 경우에 따라 공간적인 비용이 매우 크다고 생각할 수 있다.

타원 곡선 암호(ECC: Elliptic Curve Cryptography)의 256bits의 key 크기가 RSA의 1024bits와 동일한 보안 수준을 제공한다.

하지만 타원 곡선 암호 또한 단점이 존재한다.

타원 곡선 암호의 대표적인 예로 Elgamal 암호 시스템을 보면 plain text가 타원 곡선 함수의 좌푯값이어야 한다.

Plain text를 타원 곡선 함수의 좌푯값과 맵핑한다는게 쉽지 않다는 단점을 가지고 있다.

따라서 타원 곡선 암호는 암호화보다는 디지털서명(Digital Signature)에 많이 사용된다.

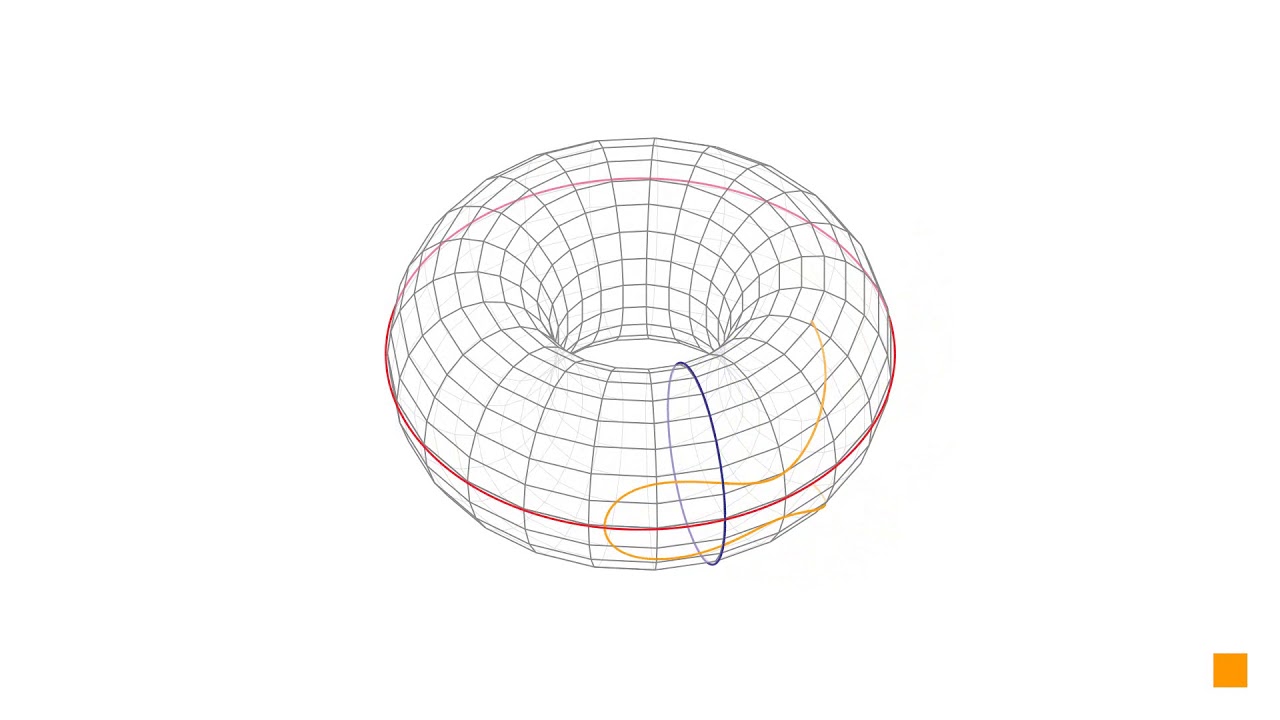
타원 곡선(Elliptic Curve)

타원 곡선의 기본 방정식은 아래 수식과 같다.

$y^{2} = x^{3} + ax + b$

하지만 실제 타원 곡선 암호에선 아래 그림과 같은 첨점(sharp point), 교차점(intersection point)이 존재하면 안 된다.

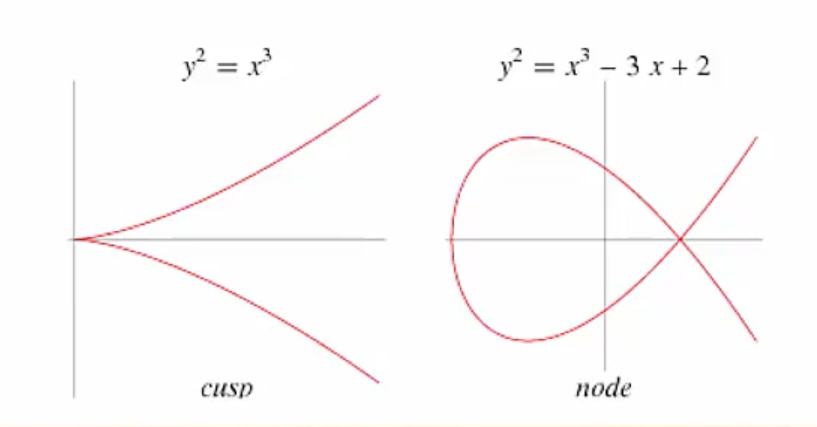
그 이유는 타원 곡선 암호에 첨점과 교차점이 존재하면 동일 점 덧셈을 할 수 없기 때문이다.

이렇게 첨점과 교차점이 존재하지 않는 타원 곡선을 비특이 타원 곡선(nonsingular elliptic curve)이라고 하고, 아래 조건을 만족하면 비특이 타원 곡선이라고 한다.

$4a^{3} + 27b^{2} \neq 0$

비특이 타원 곡선은 첨점과 교차점이 없다는 것 말고도 다른 특징도 있다.

비특이 타원 곡선의 특징은 아래와 같다.

1. 첨점(sharp point), 교차점(intersection point)이 존재하지 않는다.

2. 반드시 x축과 대칭하는 y값이 존재한다.

3. 임의의 두 점 P와 Q를 연결하는 직선에서 반드시 다른 한점이 존재한다.
   즉, 2점을 연결하는 직선에는 2점 이외에 다른 한점 또한 반드시 존재한다.

타원 곡선의 점에 대한 연산

점(Point)의 정의

타원 곡선에서 점(point)의 정의는 아래와 같다.

1. 점 P = (x, y) 좌푯값이다.

2. 점 0 = (x, 0) 이다.

3. 점 -P = (x, -y) 이다.
   이는 비특이 타원 곡선에서 반드시 존재한다.

4. 어떤 직선이 y축과 평행할 때 만나는 점을 무한점이라고 한다.

5. 무한점의 대칭점은 0점(2번 정의)라고 한다.

점 덧셈 연산

타원 곡선에서 점 덧셈 연산의 정의는 아래와 같다.

• 직선으로 연결되는 점 $P, Q, R$에 대해

1. $P + Q + R = 0$

2. $P + Q = -R$ ($-R$은 $R$의 대칭점)

3. $R + (-R) = R - R = 0$

아래 그림은 타원 곡선 점 덧셈 연산을 그래프로 표현한 것이다.

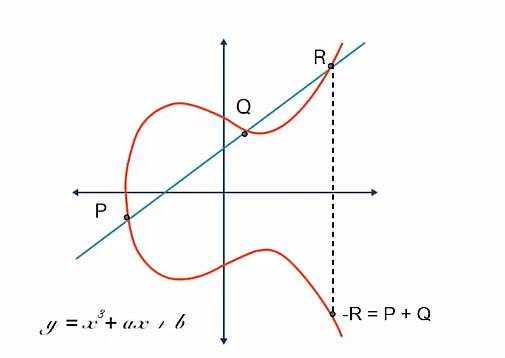
또한 동일 점을 덧셈하는 경우 즉, $P + P = 2P$의 연산에 대해서는 점$P$의 접선과 만나는 점의 대칭점을 $2P$ 라고 한다.

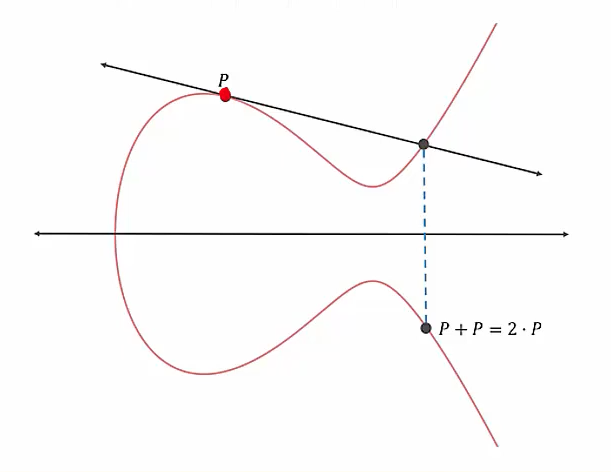
점 곱셈 연산

타원 곡선의 점 곱셈 연산은 점의 스칼라 곱셈(scalar multiplication)이다.

즉, $8 * G$는 점$G$를 8번 더한 것이다.

이때 double and add algorithm을 사용하면 효율적으로 점 곱셈 연산을 할 수 있다.

점 덧셈 연산의 방정식과 증명

점 덧셈 연산의 방정식은 아래 수식과 같다.

$m = \frac{y_{Q}-y_{P}}{x_{Q}-x{P}}$
$x_{R} = m^{2} - x_{P} - x_{Q}$
$y_{R} = m(x_{P}-x_{R}) - y_{P}$

단, 동일점 덧셈 연산에 경우엔 접점이 기울기가 되므로 기울기($m$)이 아래 방정식이 된다.

$m = \frac{3*x_{P}^2 + a}{2*y_{P}}$

위 방정식들에 대한 증명은 이전에 정리한 파일이 있다.

아래 그림들이 위 방정식에 대한 증명이다.

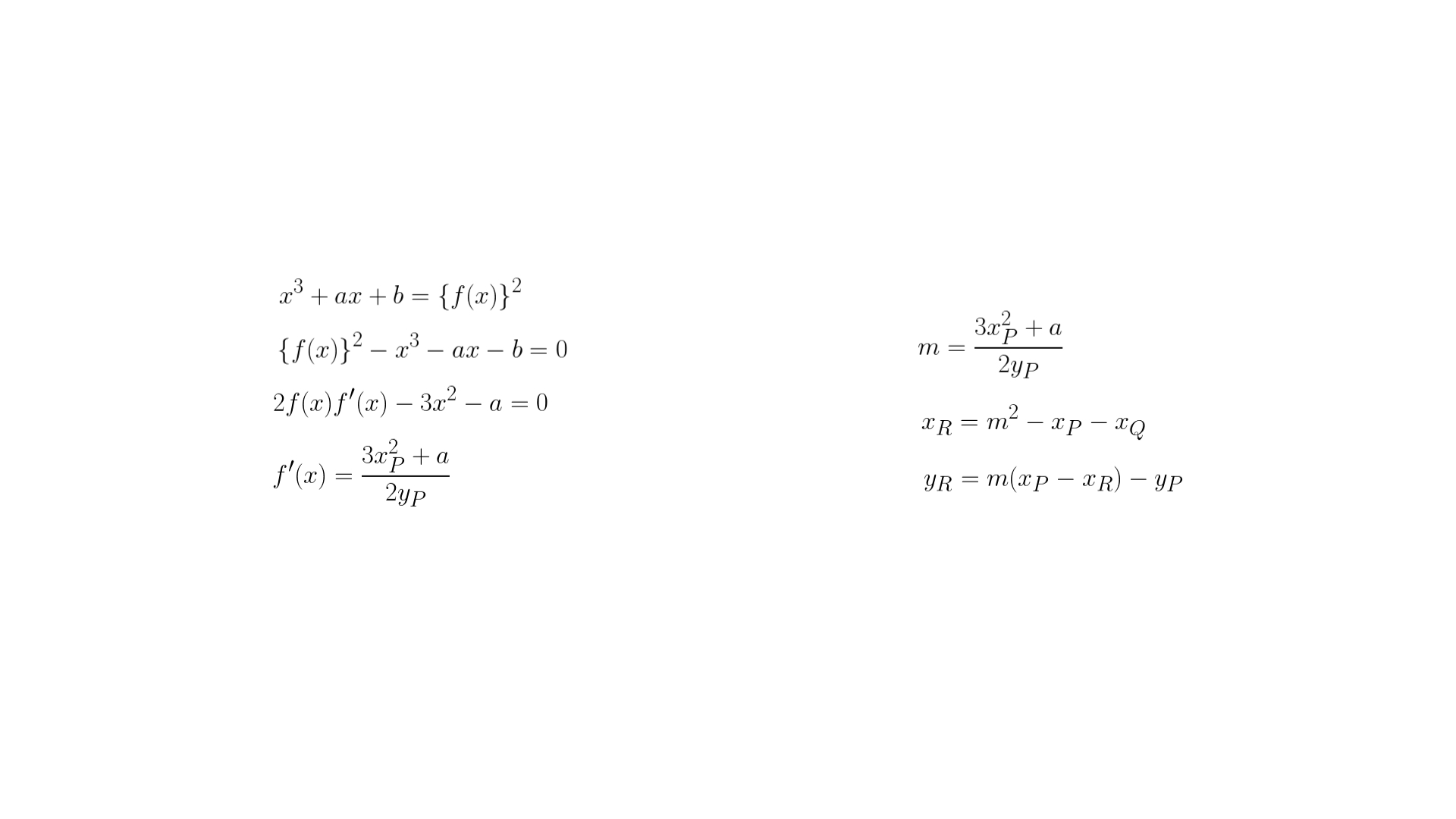
유한체 타원 곡선

실제 암호학에서는 타원 곡선에 $\mod p$ (이때 $p$는 소수) 하여 유한체 타원 곡선을 사용한다.

유한체 타원 곡선 방정식은 아래와 같다.

$y^{2} = (x^{3} + ax + b) \mod p$ ($p$는 소수)

따라서 점 덧셈 연산의 방정식 또한 아래처럼 바뀐다.

$m = \{(y_{Q}-y_{P}) * (x_{Q}-x{P})^{-1}\} \mod p$
$x_{R} = (m^{2} - x_{P} - x_{Q}) \mod p$
$y_{R} = \{m(x_{P}-x_{R}) - y_{P}\} \mod p$

$m = \{(3*x_{P}^2 + a) * (2*y_{P})^{-1}\} \mod p$

위 연산에서 나눗셈과 뺄셈은 modulo에 대한 inverse이다.

따라서 기울기를 구할 땐 extended euclidean algorithm을 사용하면 된다.