Deep residual learning for image recognition

3. Deep Residual Learning

3.1 Residual Learning

겹겹이 쌓인 층의 H(x)-x에 mapping을 F(x)+x로 재구성하는 것은, 성능 저하 문제를 해결하기 위함이다.

실제 상황에서 H(x)가 최적의 identity mapping이 아닐지라도, 이 재구성은 문제에 전제조건을 제공하는 효과를 준다. 만약 최적의 기능이 zero mapping보다 identity mapping에 더 가깝다면, solver가 identity mapping을 참조하여 작은 변화 F(x)를 학습하는 것이 새로운 기능을 처음 학습하는 것보다 쉬울 것이다. 실험에서는 학습된 residual function에서 일반적으로 작은 반응이 있다는 결과를 보여준다(Fig.7 참조). 이 결과는 identity mapping이 합리적인 전처리를 제공한다는 것을 시사한다.

H(x)가 최적의 identity라는 것은 얕은 모델의 성능이 깊이의 증가로 얻을 수 있는 성능의 상한이 된다는 말로, 모델의 깊이에 대한 일반적인 상식과 반대되는 결과이다.
재구성된 식 F(x)+x는 identity mapping이 최적의 경우를 가정하여 구성한 것으로 보인다.
그러나, 이는 가정일 뿐 실제로 깊이가 깊어질수록 성능의 향상을 기대하는 경우엔 H(x)가 최적의 identity라고 보기 어렵다.
그럼에도 F(x)+x라는 식에서는 입력 x가 학습 시에 일종의 지침으로써 작용하여 학습을 도와주므로, 최적의 identity가 아닌 경우라도 이 재구성은 여전히 긍정적인 효과를 기대할 수 있는 것이다.

3.2 Identity Mapping by Shortcuts

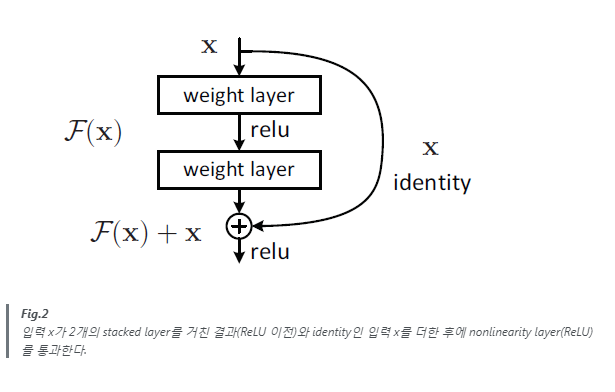
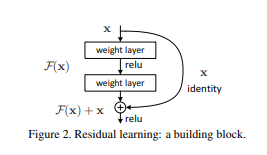
이 논문에서는 쌓여진 소수의 층들마다 Residual Learning을 사용한다. 그 building block은 위의 Fig.2에서 보였으며 논문에서는 이를 Eqn(방정식).1와 같이 정의했다.

Eqn.1

y = F(x, {Wi}) + x

x와 y는 각각 building block에서 input과 output이다. F(x, {Wi})는 학습되어야 할 residual mapping을 나타낸다. Fig.2와 같이 layer가 두 개 있는 경우를 예로 들면, F = W2σ(W1x)로 나타낼 수 있다. 여기서 σ는 ReLU를 나타내며, bias는 표기법 간소화를 위해 생략된다. F + x 연산은 shortcut connection 및 element-wise addition으로 수행되며, addition 후에는 second nonlinearity로 ReLU를 적용한다.

Eqn.1의 shortcut connection 연산은 별도의 parameter나 computational complexity가 추가되지 않는다. 이 특징은 plain network와 residual network 간의 공정한 비교를 가능하게 해준다.

element-wise addition 연산은 무시해도 될 정도이므로 공정한 요소로 인정한다.

Eqn.1에서 F + x 연산은 둘의 dimension이 같아야 하며, 이를 위해 linear projection Ws을 수행할 수 있다. 이는 Eqn.2와 같이 정의된다.

Eqn.2

y = F(x, {Wi}) + Wsx

또한, Eqn.1에서 square matrix인 Ws를 사용할 수도 있다. 하지만, 성능 저하 문제를 해결하기에는 identity mapping만으로도 충분하고 경제적이라는 것을 실험에서 보여준다. 따라서 Ws는 dimension matching의 용도로만 사용한다.

identity인 x를 mapping하기 전 feature를 한 번 더 추출하는 layer를 거친 후에 mapping 할 수도 있다는 뜻으로 보인다. 하지만 이렇게 하지 않아도 성능 저하 문제를 해결하기엔 충분하기 때문에 Wsx는 단순히 F와의 dimension matching을 위한 연산일 뿐이다.
위 식은 표기법 간소화를 위해 FC layer 상에서 표현한 것이며, conv layer 상에서도 마찬가지로 identity mapping을 구현할 수 있다. 이 경우에는 dimension matching을 위해 1x1 filter의 conv layer를 이용하며, element-wise addition은 feature map 간의 channel-by-channel addition으로 수행된다.

Projection은 현재 데이터와 다른 차원에서 보기 위한 것으로 생각하면 된다. FC layer 상에서 이 projection이 필요한 경우는 다음과 같다.

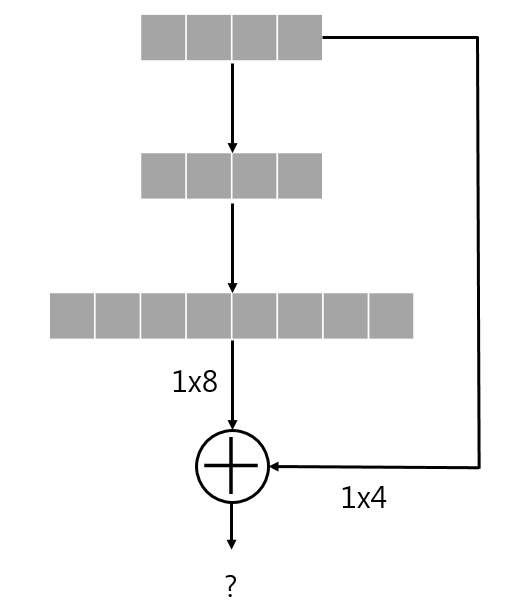
shortcut을 통해 출력과 2-layer 전의 입력의 dimension이 달라, addition이 불가능하다.

위의 unmatched dimension 문제를 해결하기 위해 projection 과정을 추가하는 것은 다음과 같은 과정으로 볼 수 있다.

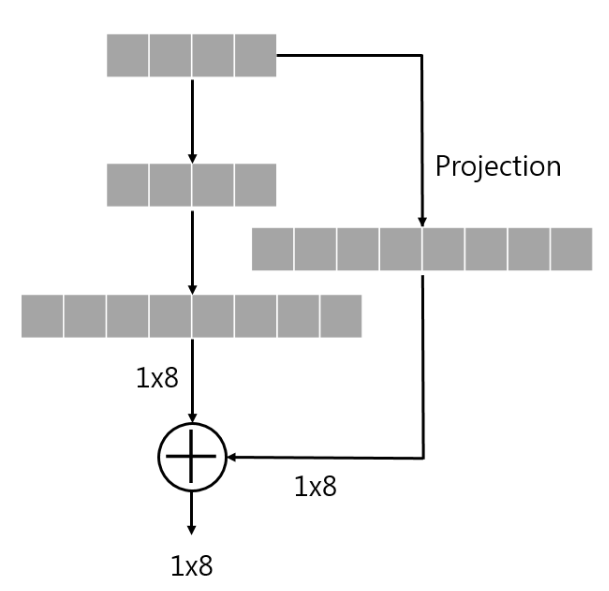
projection 과정을 통해 둘의 dimension을 맞춘 후에 addition을 진행한다.
FC layer 상에서는 이와 같이 node의 개수만 맞추면 되지만, conv layer의 경우에는 feature map size와 channel의 개수까지 맞춰야 한다.

residual function인 F의 형태는 유연하게 결정할 수 있다. 즉, 본문에서는 2~3개의 layer가 포함된 F를 사용하지만, 더 많은 layer를 포함하는 것도 가능하다. 하지만, F가 하나의 layer만 갖는 경우에는 별도의 advantage를 측정하지 못했으며, 단순 linear layer와 유사한 것으로 보인다.

3.3 Network Architectures

이 논문에서는 다양한 형태의 plain/residual network에 대해 테스트 했으며, 일관된 현상을 관찰한다. 실험에서 ImageNet dataset을 위한 두 모델을 다음과 같이 정의했다.

Plain network

baseline은 주로 VGG net(Fig.3 왼쪽)의 철학에 영감을 받았다. conv layer는 대개 3x3 filter를 가지며, 두 가지의 간단한 규칙에 따라 디자인 된다.

• 동일한 output feature map size에 대해, layer는 동일한 수의 filter를 갖는다.

• feature map size가 절반인 경우, layer 당의 time complexity를 보전하기 위해 filter의 수를 2배로 한다.

downsampling 시에는 strides가 2인 conv layer를 사용했으며, 네트워크의 마지막에는 GAP와 activation이 softmax인 1000-way FC layer로 구성된다. 이 plain network는 VGG-19에 비해 적은 수의 filter와 낮은 complexity가 가진다.

34개의 layer로 구성된 이 baseline plain network(Fig.3 가운데)는 3.6 billion FLOPs이며, 이는 VGG-19(19.6 billion FLOPs)의 18%에 불과하다.

Residual network

위 plain network를 기반으로, shortcut connection을 삽입하여 residual version의 network를 만든다. (Fig.3 오른쪽)

identity shortcut(Eqn.1)은 input과 output이 동일한 dimension인 경우(Fig.3의 solid line shortcuts)에는 직접 사용될 수 있으며, dimension이 증가하는 경우(Fig.3의 dotted line shortcuts)에는 아래의 두 옵션을 고려한다.

• zero entry를 추가로 padding하여 dimension matching 후 identity mapping을 수행한다. (별도의 parameter가 추가되지 않음)

• Eqn.2의 projection shortcut을 dimension matching에 사용한다.

shortcut connection이 다른 크기의 feature map 간에 mapping될 경우, 두 옵션 모두 strides를 2로 수행한다.

feature map의 크기가 달라지는 경우는 strides가 2인 conv layer를 통한 downsampling을 거쳤기 때문이다.

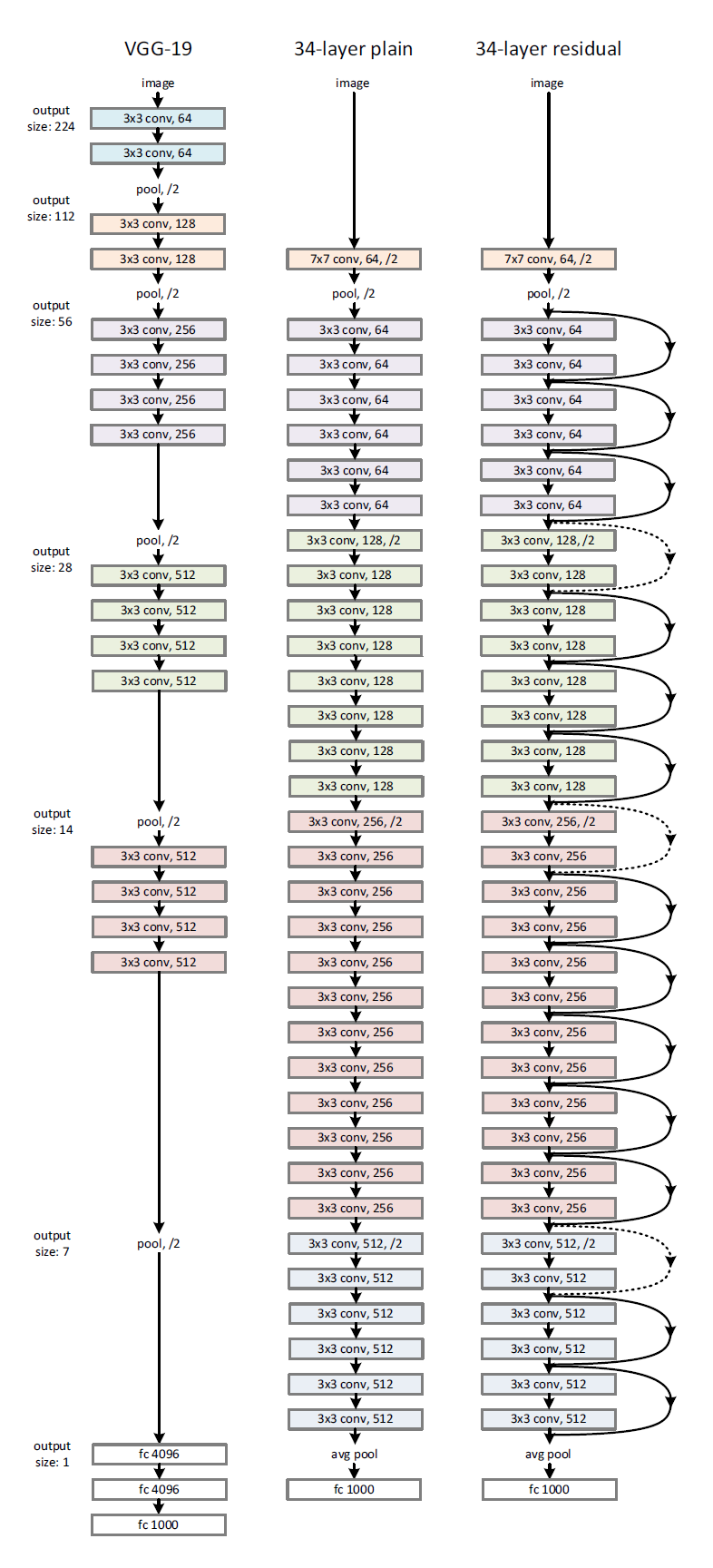
Fig.3
ImageNet dataset 학습에 사용된 network architecture
왼쪽은 VGG-19 model (19.6 billion FLOPs)
가운데는 34-layer plain network (3.6 billion FLOPs)
오른쪽은 34-layer residual network (3.6 billion FLOPs)
dotted shortcut은 dimension이 증가한 결과와 mapping하는 경우이다.

3.4 Implementation(구현)

논문에서 ImageNet dataset에 대한 실험은 AlexNet과 VGG의 방법을 따른다. 이미지는 scale augmentation를 위해 [256, 480]에서 무작위하게 샘플링 된 shorter side를 사용하여 rescaling된다. 224x224 crop은 horizontal flip with per-pixel mean subtracted(픽셀당 평균을 뺀 수평 뒤집기)을 이미지 중에 무작위로 샘플링 되며, standard color augmentation도 사용된다.

언급된 기법(horizontal flip, per-pixel mean subtract, standard color augmentation)들로 data augmentaion을 수행하여 학습한다는 말이다.

• 각각의 conv layer와 activation 사이에는 batch normalization을 사용하며, He initialization 기법으로 weight를 초기화하여 모든 plain/residual nets을 학습한다.

• batch normalization에 근거해 dropout을 사용하지 않는다.

• learning rate는 0.1에서 시작하여, error plateau 상태마다 rate를 10으로 나누어 적용하며, decay는 0.0001, momentum은 0.9로 한 SGD를 사용했다.

• mini-batch size는 256로 했으며, iteration은 총 600K회 수행된다.

비교를 위해 AlexNet의 standard 10-crop test를 수행했다. 최상의 결과를 내기 위해, VGG와 He initialization(ReLU를 위해 만들어진 초기화 방법)에서 사용한 fully-convolutional form을 적용했으며, multiple scale에 대한 score를 평균했다.

fully-convolutional form은 정적인 크기를 가지는 FC layer를 제외하여 다양한 크기의 입력을 처리할 수 있는 방법이다. 자세한 설명은 OverFeat논문을 참조하자. VGG와 He initialization 둘 다 이 논문의 방법을 사용한다.
multiple scale은 shorter side가 {224, 256, 384, 480, 640}인 것으로 rescaling하여 사용한다.