오늘은 '밑바닥부터 시작하는 딥러닝'이란 책과 아래 Reference를 바탕으로 정리를 할 예정입니다.
Reference
📕 밑바닥부터 시작하는 딥러닝, 한빛미디어
🔗 참고 포스팅
🔗 참고 포스팅2
🔗 이미지 출처1
🔗 이미지 출처2
🔗 이미지 출처3
Contents
- Reference
- Weight decay
- zero initialization
- Random initialization
- Xavier Initialization
- He Initialization
신경망 학습에서 특히 중요한 것이 가중치의 초깃값입니다.
가중치의 초깃값을 무엇으로 설정하느냐가 신경망 학습에 영향을 많이 끼치는데요. 그 이유는 각 neuron의 가중치를 기반으로 error를 결정하기 때문이고, 정확한 모델을 얻으려면 작은 error를 필요로 하기 때문입니다.
이번 개념은 neural network, weight, bias, activation function, forward pass, backpropagation 등의 개념에 익숙함을 전제로 진행됩니다.
해당 내용에 대해 알아보겠습니다.
Weight decay
그전에 Weight decay에 대해 설명하고 시작하겠습니다. 가중치 감소(weight decay) 기법은 overfitting을 억제해 성능을 높이는 기술입니다.
Weight decay는 loss function에 L2 norm과 같은 penalty를 추가하는 정규화 기법입니다.
그리고 bias가 아닌 weight에만 decay를 적용하는 것을 더 선호합니다.
Weight decay를 사용하는 이유가 무엇일까요?
그 효과로
- Overfitting을 방지합니다.
- weight을 작게 유지합니다. 이는 gradient exploding을 방지합니다.
weight의 L2 norm이 loss에 추가되기 때문에 네트워크의 각 반복은 loss 외에 model weight를 최적화하려고 시도합니다.
weight을 작게 유지하면 가중치가 엄청 커지며 exploding되는 것을 방지하기 때문입니다.
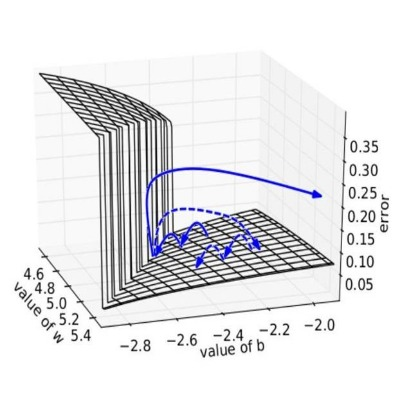
weight을 작게 만들고 싶으면 초깃값도 최대한 작게 시작하는 방법이 있습니다.
지금까지는 0.01 * np.random.randn(10,100)처럼 정규분포에서 시작되는 값을 0.01배 한 작은 값(표준편차가 0.01인 정규분포)을 사용했습니다.
그렇다면 가중치의 초깃값을 모두 0으로 설정한다면 어떻게 될까요?
zero initialization
결론적으로 0으로 초기화 시키는 방법은 아주 나쁜 방법입니다. 0으로 초기화하면 제대로 학습되지 않습니다.
그 이유로는 neuron이 training 중에 동일한 feature를 학습하게 때문인데요.
순전파 때 입력의 모든 가중치가 0이라면 두 번째 층 neuron이도 똑같은 값이 전달됩니다. 이 의미는 backpropagation에서 모든 weight의 값이 모두 똑같이 바뀌게 됨을 뜻합니다.
ⅰ) e.g.
조금 더 구체적으로 예를 들어 설명하겠습니다.
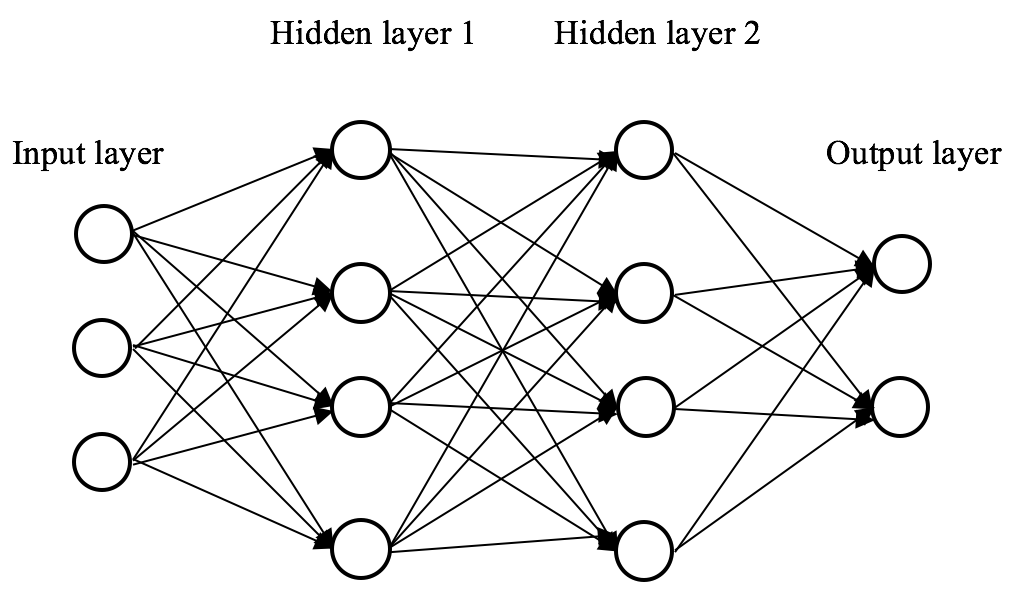
2개의 hidden layer가 있는 neural network를 고려해보겠습니다.
모든 bias를 0으로 초기화하고 weight을 일정한 로 초기화합니다.
이 network에서 입력 를 전달하면 두 hidden layer의 출력은 가 됩니다.
따라서 두 hidden layer는 loss에 동일한 영향을 미치므로 동일한 기울기가 발생합니다.
따라서 두 neuron은 훈련 전반에 걸쳐 대칭적으로 계산되어 서로 다른 neuron이 서로 다른 것을 학습하는 것을 막습니다.
대칭적으로 계산된다는 것의 의미?
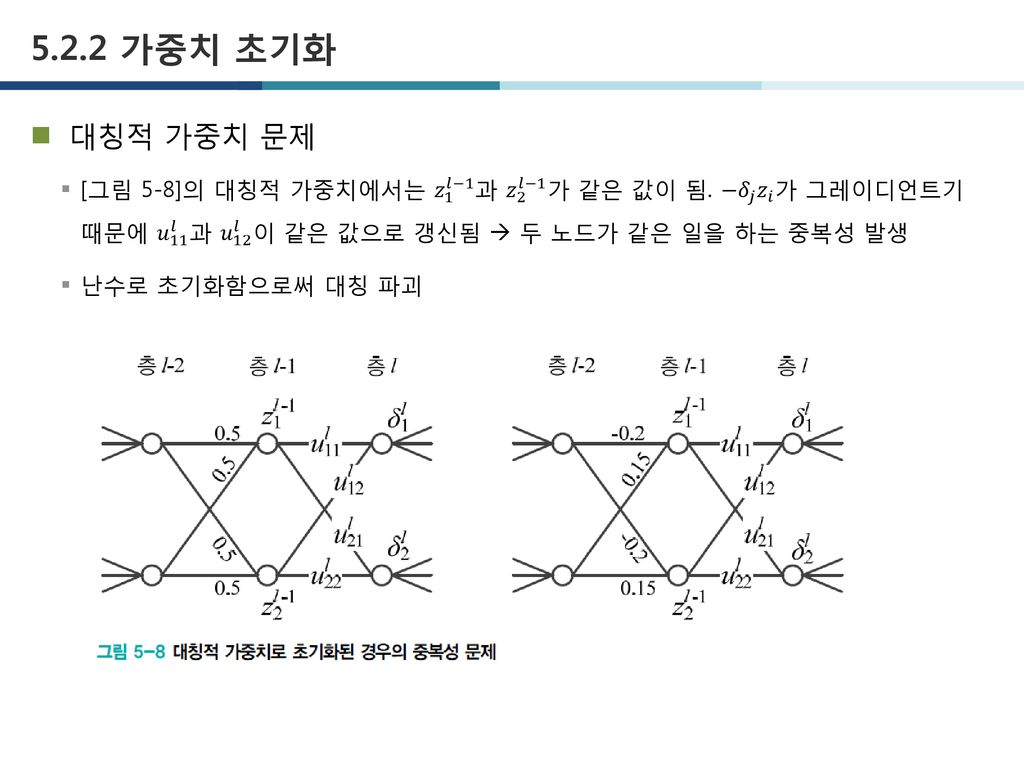
이미지 출처: 5장. 딥러닝 최적화
이를 가중치가 고르게 되어버리는 상황이라고도 표현합니다.
그렇게 되면 weight이 여러 개 있는 의미가 사라지게 돼서 아무 의미가 없습니다.
이 방법을 막으려면 무작위로 설정하는 방법이 있습니다.
Random initialization
weight에 random한 값을 주는 것은 초깃값을 0으로 주는 것보단 낫습니다. 하지만 weight을 초기화하는 것은 매우 높거나 매우 낮은 값을 가지게 됩니다.
이때 hidden layer에서 활성화값(activation function의 출력 데이터)의 분포를 관찰하면 중요한 정보를 얻을 수 있습니다.
구체적으로 활성화 함수로 Sigmoid를 사용하는 5층 layer를 가진 neural network이며, random하게 생성한 input data를 통해 활성화값의 분포를 히스토그램으로 살펴보겠습니다.
(i) vanishing gradient
모델의 weight을 가우시안 분포 을 따르는 값으로 랜덤하게 초기화를 했다고 가정합니다.
import numpy as np
import matplotlib.ptplot as plt
def sigmoid(x):
return 1 / (1+np.exp(-x))
x = np.random.randn*1000, 100) # 1000개의 데이터
node_num = 100 # 각 은닉층의 노드 수
hidden_layer_sioze = 5 # 은닉층이 5개
activations = {} # 이곳에 활성화값을 저장
for i in range(hidden_layer_size):
if i !=0:
x = activations[i-1]
w = np.random.randn(node_num, node_num) * 1
a = np.dot(x, w)
z = sigmoid(a)
activations[i] = z- 총 5개의 layer
- 각 layer의 neuron 수는 100개
- 을 따르는 1,000개의 input data
- activation function: sigmoid
activations변수에 활성화값이 저장
이 경우에는 표준편차가 1인 가우시안 분포를 이용했는데, 이 분포된 정도를 바꿔가며 활성화값들의 분포가 어떻게 변화하는지를 관찰합니다.
for i, a in activations.items():
plt.subplot(1, len(activations), i+1)
plt.title(str(i+1) + '-layer')
plt.hist(a.flatten(), 30, range(0,1))
plt.show()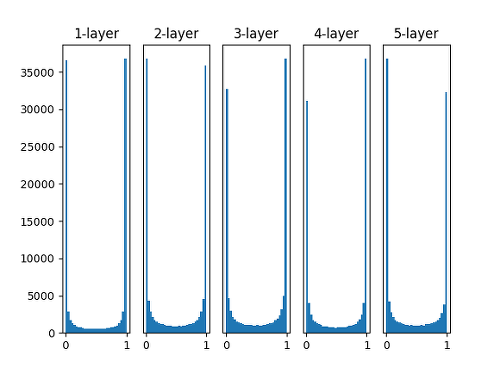
위 그림을 보면 활성화값이 0과 1에 치우쳐서 분포되어 있습니다.
여기서 사용된 sigmoid 함수는 출력이 0에 가까워지거나 1에 가까워지면 그 미분 값은 0에 가까워지게 됩니다.
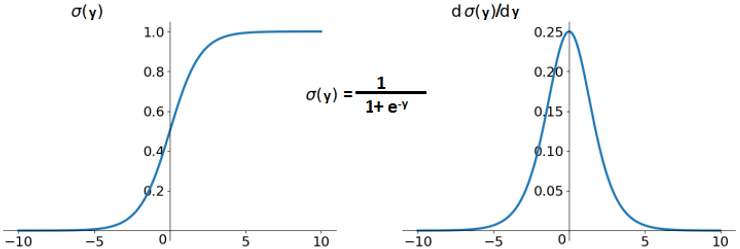
그래서 데이터가 0과 1에 치우치면 backpropagation 때 gradient가 점점 작아지다가 아예 사라지게 됩니다.
이것을 gradient vanishing이라 말합니다.
(ii) case 2
이번에는 모델의 weight을 가우시안 분포 을 따르는 값으로 랜덤하게 초기화를 했다고 가정합니다.
# w = np.random.randn(node_num, node_num) *1
w = np.random.randn(node_num, node_num) * 0.01결과를 바로 살펴보겠습니다.
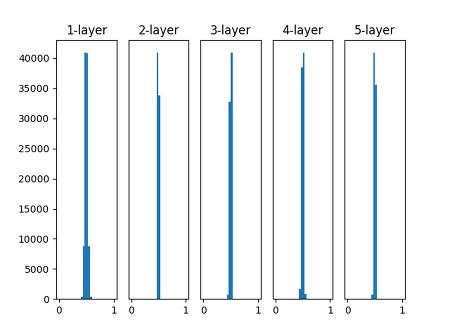
이번에는 반대의 그림이 나왔습니다. 0.5의 부분에 집중되어 있는데요.
gradient vanishing의 문제는 나타나지 않았지만, 활성화값이 치우쳤다는 것은 표현력의 관점에서 큰 문제가 있는 것입니다.
이 의미는 많은 뉴런이 거의 같은 값을 갖고 있다는 뜻이며, 아까 zero initialization에서 설명한 것과 같이 같은 값을 가지면 뉴런을 여러 개 둔 의미가 사라지게 됩니다.
그래서 활성화값이 치우치는 것을 표현력을 제한한다는 점에서 문제가 발생합니다.
여기까지 여러가지 case를 살펴보며 네트워크 활성화의 기울기 문제(vanishing, exploding)을 막기 위해 다음과 같은 결론을 내릴 수 있습니다.
- activation의 평균은 0이어야 합니다.
- activation의 variance는 모든 layer에서 동일하게 유지되어야 합니다.
저는 여기서 1번과 2번의 내용이 이해가 잘 되지 않았는데요.
잠깐만 살펴보고 가겠습니다.
1번의 경우
딥러닝에서 zero-centered 속성을 같는 activation functin이 중요합니다.
이 활성화 함수는 평균 활성화값을 0이 되도록 만듭니다.
정규화된 데이터에서 작동하는 모델이 더 빠른 수렴(convergence)을 하기 때문인데요.
zero-centered 속성을 갖는 활성화 함수는 입니다. 하지만 하이퍼볼릭 탄젠트는 점근선에서 saturated하는 속성을 갖고 있습니다.
이는 gradient가 시간이 지남에 따라 점점 작아져서 training하며 약해집니다.
ReLU는 이 문제를 피하지만 zero-centered가 아닙니다. 따라서 ReLU를 위한 weight initialization 기법이 만들어졌고, 많은 딥러닝 연구자들이 이 문제를 완화하기 위해 수많은 normalization layers를 만들었습니다.
예를 들면, batch norm, layer norm, weight norm 등이 있습니다.
2번의 내용은 layer가 늘어나더라도 activation value(활성화값)이 saturation되지 않는 곳(sigmoid의 경우는 0.5)에서 평균과 표준편차가 일정하기를 바란다는 의미입니다.
sigmoid를 사용하면 output의 값이 0과 1에 가깝다면 saturation한 상황에 걸려 training이 잘 안 된다는 것을 떠올릴 수 있습니다.
그 원인을 activation value가 일정하지 않기 때문에 발생하는 문제라 생각했는데요.
layer를 늘리더라도 activation vlaue가 평균과 표준편차가 일정하게 유지되도록 weight을 초기화하면 layer를 무한하게 쌓을 수 있다는 이론적인 결론을 내렸습니다.
다시 정리하자면, 이전 layer의 activation value와 l다음 layer의 activation의 평균과 표준편차가 일정해야 함을 의미합니다.
지금부터는 위에서 언급한 내용에 따라 이 문제를 해결할 수 있는 여러 초기화 기법을 설명할 예정입니다.
Xavier Initialization
Xavier Initialization은 각 layer의 활성화값을 더 광범위하게 분포시킬 목적으로 weight의 적절한 분포를 찾으려 했습니다.
또한, tanh 또는 sigmoid로 활성화 되는 초깃값을 위해 이 방법을 주로 사용합니다.
이전 layer의 neuron의 개수가 이라면 표준편차가 인 분포를 사용하는 개념입니다.
너무 크지도 않고 작지도 않은 weight을 사용하여 gradient가 vanishing하거나 exploding하는 문제를 막습니다.
Xavier Initialization을 사용하게 된다면, 뉴런의 개수가 많을수록 초깃값으로 설정하는 weight이 더 좁게 퍼짐을 알 수 있습니다.
node_num = 100 # 이전의 neuron 수
w = np.random.randn(node_num, node_num) / np.sqrt(node_num)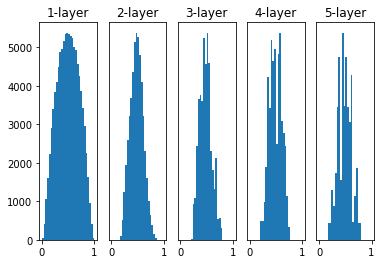
Xavier Initialization을 사용하면 위의 그래프처럼 됩니다.
이 결과는 layer가 더 깊어질수록 앞에 본 방식보다 더 넓게 분포됨을 알 수 있습니다.
데이터가 더 적당히 넓게 펴지므로 sigmoid 함수를 사용할 때도 표현을 제한 받지 않고 학습이 가능합니다.
또한, neuron의 개수에 따라 weight이 초기화되기 때문에 고정된 표준편차를 사용할 때보다 더 robust한 성질을 가집니다.
Xavier Initialization는
tanh 또는 sigmoid로 활성화되는 경우라 가정(선형성)
하고 초기화된 값인데요.
tanh 또는 sigmoid와 잘 맞는 이유도 두 함수는 좌우 대칭이라 중앙 부분이 선형인 함수로 볼 수 있기 때문인데요.
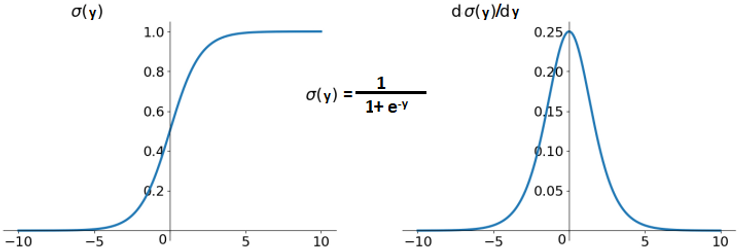
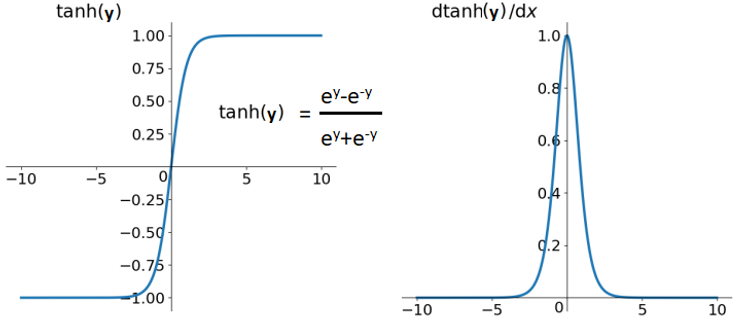
반면 ReLU를 이용할 때는 비선형성(nonlinearity)이 발생해서 멈추게 됩니다.

activation function으로 ReLU로 학습하게 될 경우 아래와 같이 학습됩니다.
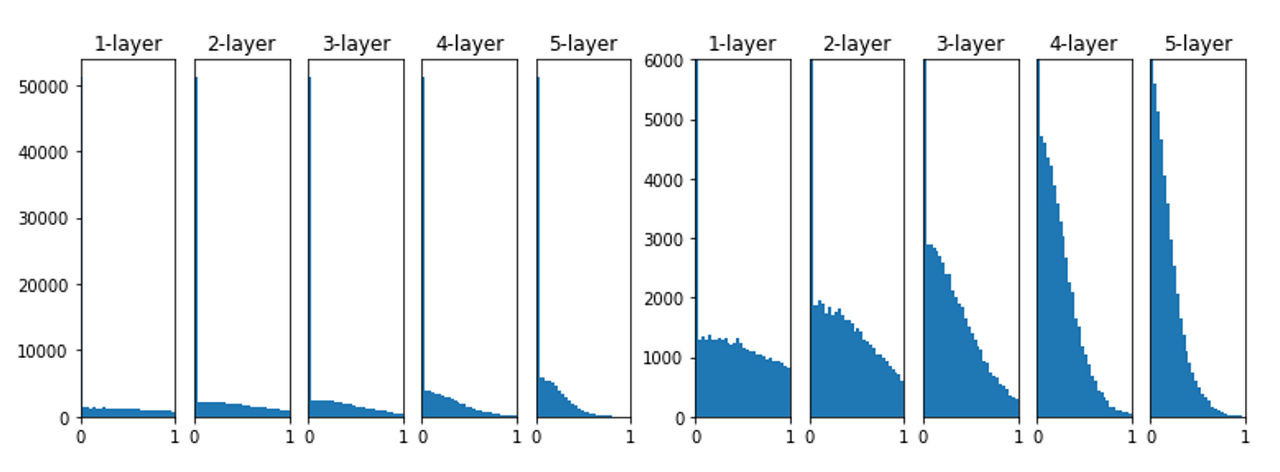
layer가 깊어지면서 조금씩 더 치우친다는 것을 볼 수 있습니다.
그리고 만약 표준편차가 0.01인 weight 값을 갖게 된다면
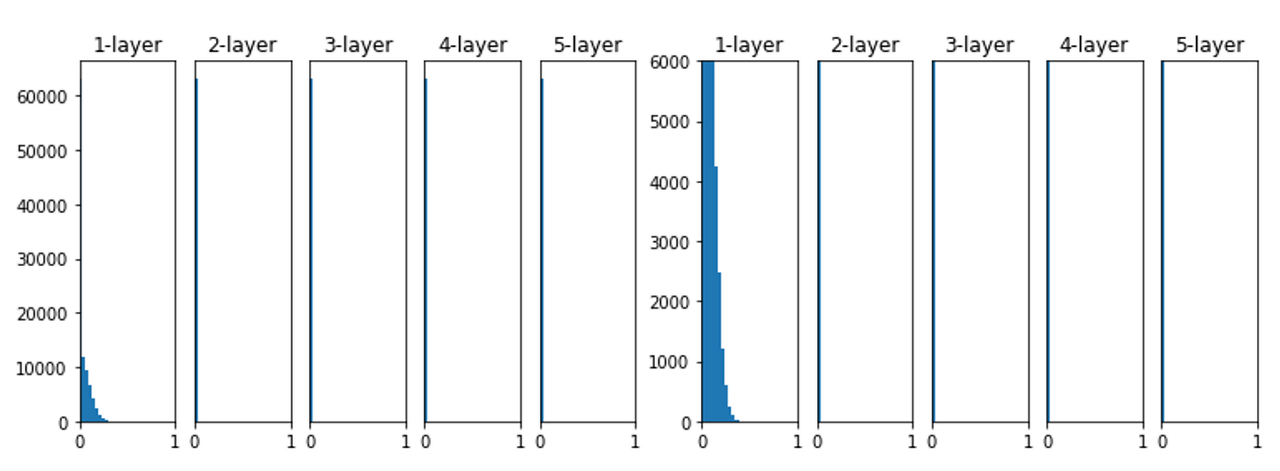
데이터가 아예 한쪽으로 치우치게 되며 제대로 학습되지 않음을 확인할 수 있습니다.
이도 마찬가지로 backpropagation을 할 때 아주 작은 weight으로 인해 gradient 역시 작아지며 똑같이 vanishing 문제를 갖게 됩니다.
이러한 문제로 제안된 방법이 He Initialization입니다.
He Initialization
He Initialization는 를 위해 만들어진 초기화 방법입니다.
이 특화된 초깃값은 Kaiming He의 이름을 따서 He Initialization라고 부릅니다.
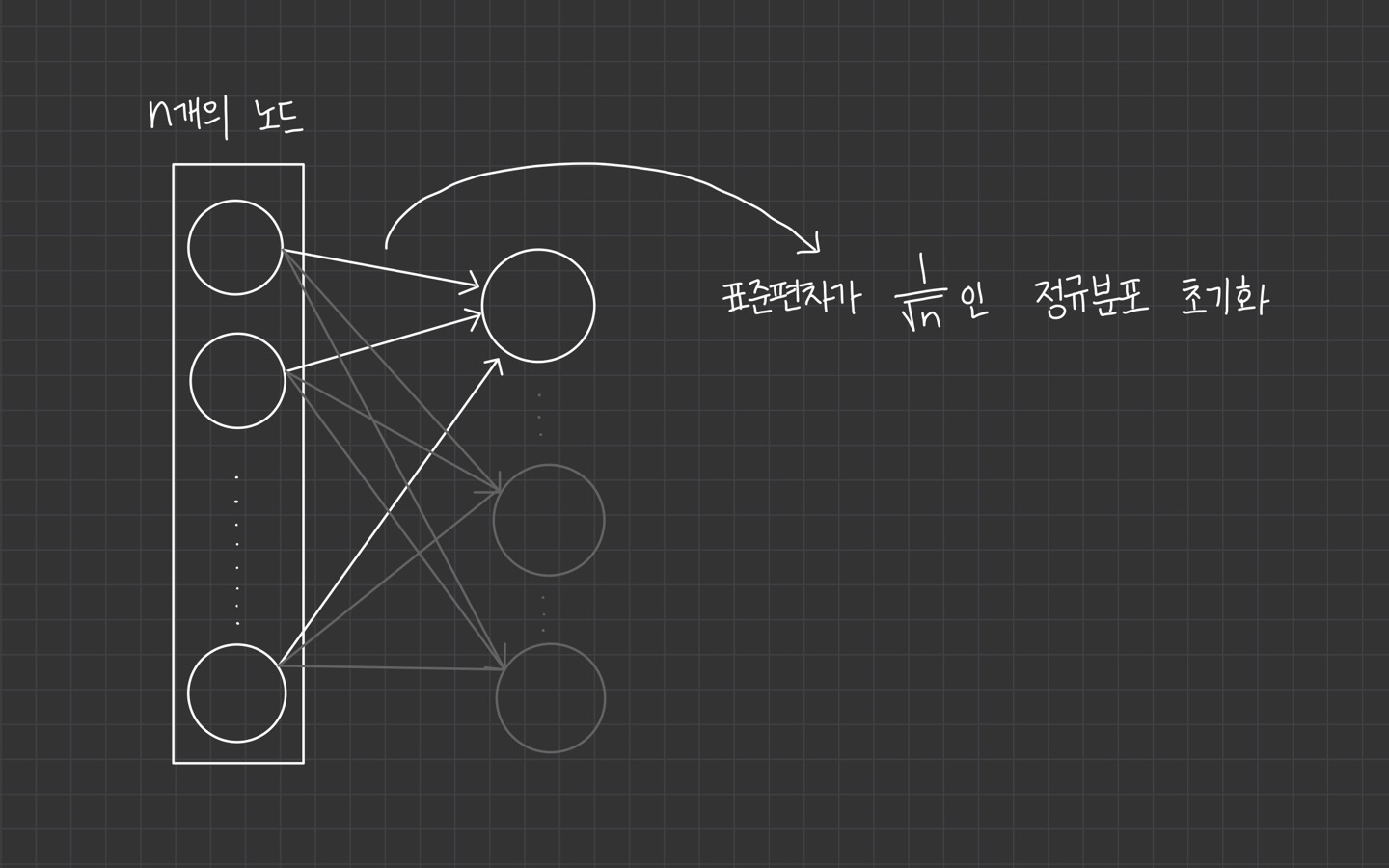
He Initialization는 앞 layer의 neuron이 n개일 때, 표준편차가 인 정규분포를 사용합니다.
Xavier Initialization의 초깃값이 이었습니다.
ReLU는 음의 영역이 0이라서 활성화되는 영역을 더 넓게 분포시키기 위해 2배의 계수가 필요하다고 해석하면 됩니다.

activation function으로 ReLU를 이용한 경우의 activation 분포를 살펴보면
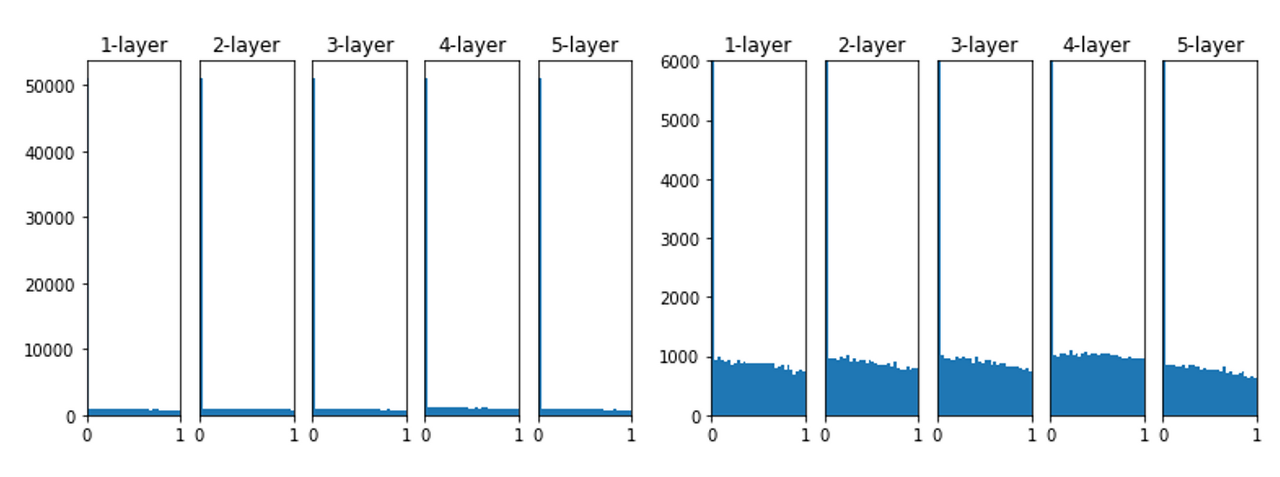
위와 같습니다.
He Initialization은 모든 layer에서 균일하게 분포되어 있음을 알 수 있습니다.
그래서 backpropagation 때도 적절한 값이 나올 것이라 기대할 수 있습니다.
정리하면
activation function으로 ReLU를 사용하면 He 초깃값을 쓰는 것이 좋습니다.
여기까지 초기화를 위해 살펴본 방법은 좋은 시작점 역할을 하면서 gradient의 vanishing, exploding 문제를 완화시킵니다.
이건 느린 convergence를 피하는데 도움이 되고, 최솟값에서 계속 진동하는 현상도 막아줍니다.
Weight Initialization의 주요 목적은 parameter의 분산을 최소화하는 것입니다.
여기까지 내용을 정리하고 마무리하겠습니다!
*(22.07.07) 내용 수정
activation function으로 ReLU를 사용하면 He 초깃값을 쓰는 것이 좋습니다.


좋은글 감사합니다. 많이 배웠습니다.