Lecture 9 | CNN Architectures(65~)

Hoon82의 velog·2022년 8월 23일

ResNet

ResNet(레즈넷)은 revolution(혁명)이라고 할 만큼 네트웍이 깊어집니다. 무려 152개의 레이어를 지닌 아키텍쳐입니다.

우선 연구자들은 layer의 깊이와 성능이 비례하는지에 대해 "깊이가 깊어질수록 성능이 좋아지는게 맞는걸까?"라는 의문을 가졌습니다.

결과는 그렇지 않았습니다. 오버 피팅의 문제도 아닙니다. 그냥 train/test 성능이 둘 다 좋지 않습니다. ResNet(레즈넷) 저자들은 여기서 residual connection(중복 연결)의 탄생을 이끕니다.

더 깊은 모델을 세울 때 어느 순간 optimization(최적화)에서 문제가 생긴다고 생각한 겁니다. 우선 저자들은 이 문제에 어떻게 다가갔는지가 중요합니다.

깊이가 얕은 모델과 그 모델을 그대로 가져와서 깊이를 더 깊게 만드는데 깊이를 더 깊게 만들 때 추가 layer들은 identity mapping(항등 사상)을 해줍니다.(입력값이 들어오면 그대로 출력값으로 나가게끔 해준다는 의미)

그렇게 하면 적어도 얕은 깊이의 모델 성능은 나와야 될겁니다. 그렇게 핵심 아이디어인 Residual block(중복 블록)이 나옵니다.

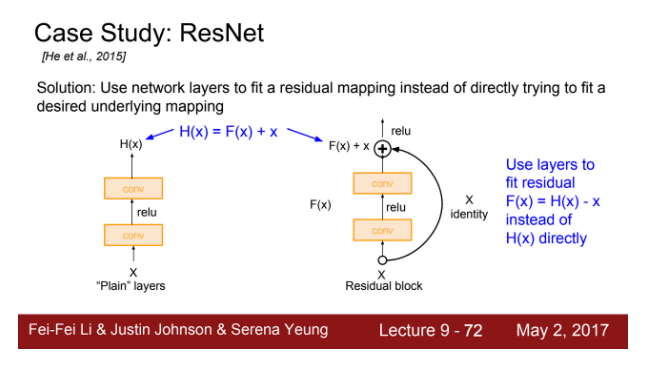
슬라이드를 보시면 기존의 층과 Residual block(중복 블록)을 넣은 층(오른쪽의 그림)의 비교입니다.

기존 출력값인 F(x)에 identity mapping(항등 사상)으로 입력값인 x를 더해줍니다. 강의에서는 F(x)를 변화량 delta(델타)라고 표현합니다.

왼쪽의 기존 layer인 H(x)로 학습하는 방식은 네트웍이 깊어질수록 학습이 어려워지고 문제가 생겼습니다. 그래서 이 구조를 깨버리고 변화량인 F(x)를 학습하는 Residual block(중복 블록)을 설계한 것입니다.

F(x) = H(x) - x이고 변화량인 F(x)를 residual(중복)이라고 표현할 수 있습니다. 그래서 이 아키텍쳐는 ResNet(레즈넷)이라는 이름이 붙게 된 것입니다.

네트웍이 깊어질수록 과적합 문제가 아니라 optimization(최적화)에서 문제가 일어나기 때문에 학습 방식을 고쳤습니다.

저자들은 56층의 layer가 적어도 20층의 layer 성능이 나오면 나왔지 더 나빠지지 않도록 할 수 있는 방안을 고심했고, 그게 바로 residual block(중복 블록)인 것입니다.

20층이 사실 최고의 성능을 내는 부분이었고, 56층까지 가면서 변화량이 0이라면, residual block(중복 블록)은 나머지 층에서 계속 input=output 값을 내보내게 되는 것입니다.

이게 backward(역방향) 시에는 더해주는 상수 값인 x가 계속 존재하니까 기울기 소실의 문제도 해결하게 되는 것입니다. 가설이 먹힌 것입니다.

ResNet(레즈넷)은 기본적으로 VGG-19를 뼈대로 ConV(콘브) 계층을 추가해 layer를 깊게 만들었습니다.

3x3 ConV layer(콘브 계층)를 2개씩 쌓고 residual block(중복 블록)을 끼워 주는데, 주기적으로 필터를 2배씩 늘리고 stride(스트라이드)를 2로 두어서 downsampling(다운샘플링) 해주었습니다.

모델의 시작을 ConV layer(콘브 계층)로 해서, 모델의 마지막에는 global average pooling(글로벌 평균 풀링)으로 했습니다. 그래서 최종 1000가지 분류에 대한 입력이 됐습니다.

그리고 저자들은 34층, 50층, 101층까지의 깊이를 만들었고, 결국 이미지넷을 위해서 152층까지 설계하였습니다.

50 layer부터는 파라미터가 급격하게 많아져서 효율성을 개선하기 위해 bottleneck(병목) 계층을 이용합니다. 넘어가지 않으면 그냥 3x3 ConV(콘브) 계층을 연속해서 사용합니다.

실제 ResNet(레즈넷)은 모든 ConV layer(콘브 계층) 후에 계속해서 Batch Normalization(배치 정규화)을 사용합니다. Xavier(자비에)를 사용해서 초기화를 개선합니다.

learining rate(학습률)는 0.1에서 loss가 줄지 않으면 조금씩 줄여서 학습을 시킵니다. dropout은 없습니다.

시작할 땐 AlexNet(알렉스넷)이 있었고, VGG와 GoogleNet(구글넷)도 여전히 매우 많이 쓰입니다. 그러나 ResNet(레즈넷)이 가장 최신의 것이고 가장 잘 동작하는 모델이므로 만약 훈련시킬 새로운 모델을 찾는다면, ResNet(레즈넷)을 추천합니다.

Comparing complexity(복잡성 비교)

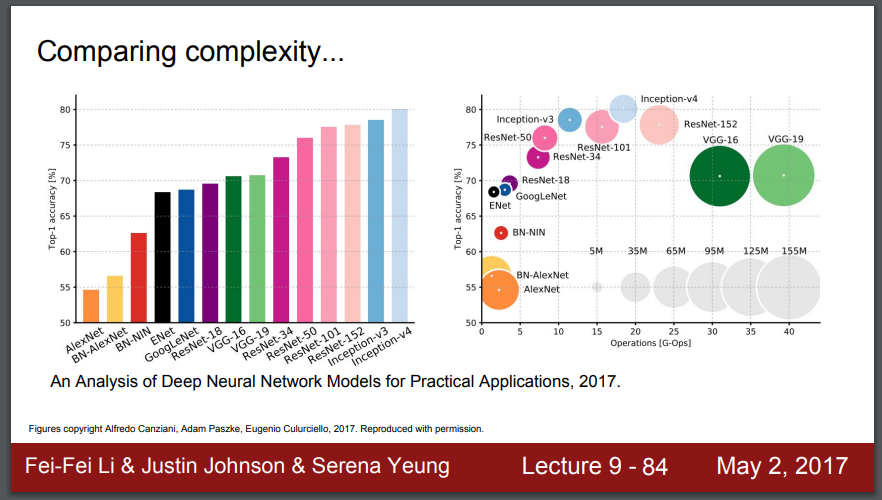
여기에 플롯(plot)들이 있습니다. 성능으로 정렬된 건데, Top 1 정확도로 정렬된 것입니다. 그래서 높은게 더 좋은 것입니다.

왼쪽을 보면, 가장 좋은 것은 인셉션-v4인데, 이건 레즈넷과 인셉션의 조합입니다.

오른쪽을 보면,

X축은 많은 연산을 할수록, 계산적으로는 더 비쌉니다. 원이 클수록, 메모리 사용이 많습니다. 회색원들이 참고용입니다.

보다시피 녹색원인 VGG들이 효율이 가장 낮습니다. 가장 큰 메모리를 사용하고, 가장 많은 연산을 합니다.

구글넷이 가장 효율적입니다. 그건 연산에서 아래에 있고, 메모리 사용에 대해서도 작은 원입니다.

알렉스넷은 초기 모델인데, 낮은 정확도를 가지고 있습니다. 작은 망이라서 비교적 작은 계산이 필요합니다. 그러나 특별히 메모리를 적게 쓰는 것은 아닙니다.

레즈넷은, 중간 정도로 효율적입니다. 메모리와 연산 측면에서 모두 중간 정도에 있습니다. 그리고 높은 정확도를 보입니다.

Forward pass time and power consumption(순방향 전달 시간과 전력 소비)

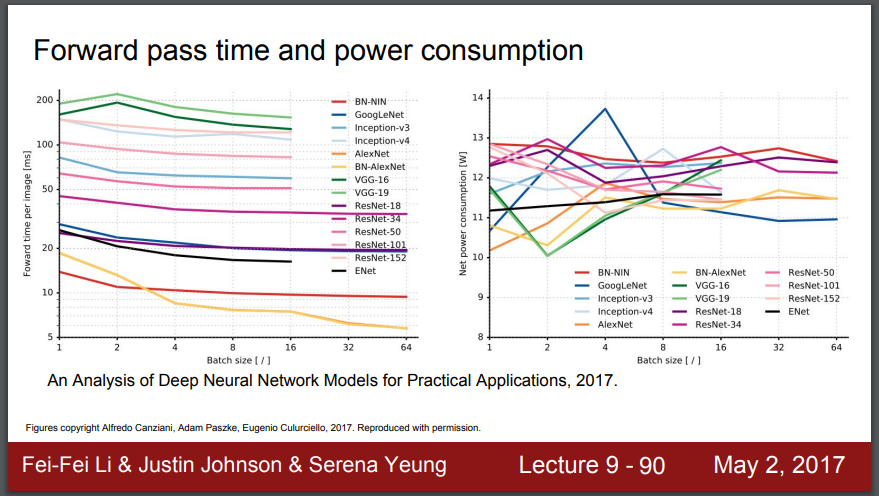
왼쪽의 플롯은 forward pass(순방향 전달) 시간을 보여줍니다. 제일 위쪽 VGG가 순방향 전달을 200밀리세컨드(milisecond)에 하는 것을 볼 수 있습니다. 1초당 5개의 프레임을 얻는 것입니다.

오른쪽의 플롯은 전력 소모를 나타냅니다.

Network in Network(NiN)

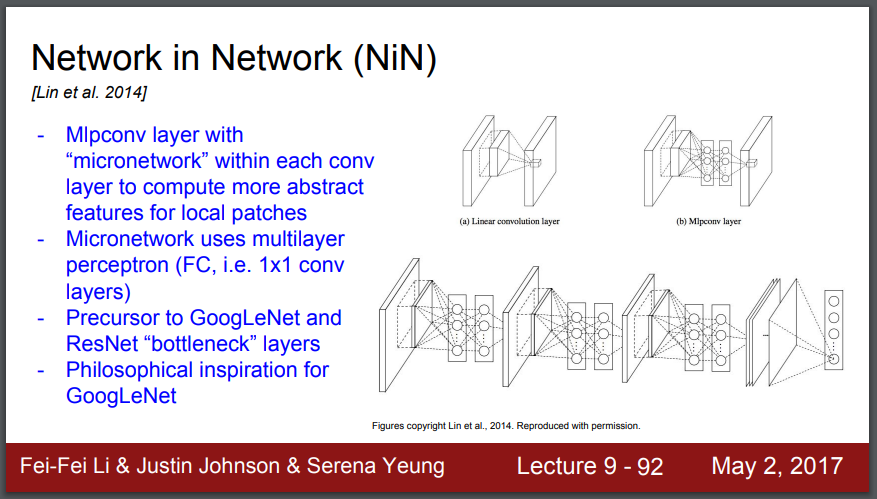
Network in Network는 마이크로 망인데 논문의 이름입니다. 여기서는 각 conv(콘브) 계층 내에서 2개의 완전 연결 계층과 함께 Mlp를 쌓으려고 합니다. 표준적인 conv(콘브) 위에 쌓는 겁니다.

그러면 이 지역적 패치(local patches)에 대한 추상적인 피쳐 (feature)에 대해 더 많이 계산할 수가 있습니다. conv(콘브) 필터를 그냥 sliding(슬라이딩)하는 대신, 더 복잡한 계층구조의 필터 집합을 슬라이딩하고 그걸 사용해서 활성 지도를 얻는 것입니다.

그건 완전 연결 계층 혹은 1 x 1 콘브 계층을 사용합니다. 각각의 계층에서 쌓여진 망 내의 망(network in network)을 얻습니다.

이걸 알아야 하는 이유는 network in network가 구글넷, 레즈넷의 선도자이고, 병목 계층 아이디어가 많이 사용되었기 때문입니다.

Improving ResNets(ResNets 개선하기)

Identity Mappings in Deep Residual Networks(깊은 중복 망에서 항등 사상)
- 블록 경로에 있던 계층들을 조정했고, 이 새로운 구조가 망을 통해 정보를 전달하기 위한 더 직접적인 경로를 가질 수 있다는 것을 보여줬습니다.
Wide Residual Networks(넓은 중복 블록)
- 더 넓은 중복 블록(Wide Residual Networks)을 사용했습니다. 이는 모든 콘브 계층에 더 많은 필터가 있다는 겁니다.
- 이전에는 계층마다 F개의 필터를 가지고 있었고 이 k인수를 사용했습니다. 그리고 모든 계층에서 F 곱하기 k 필터가 된다고 얘기합니다.
- 그래서 이 더 넓은 계층을 사용해서 그들은 50층의 넓은 레즈넷이 152층의 원래 레즈넷을 이길 수 있다는 것을 보여줬습니다.
- 그것은 또한 추가적인 장점이 있었는데, 같은 수의 파라미터라도 그것이 계산적으로 더 효율적이라는 겁니다.
- 왜냐면 이것들을 병렬화할 수 있어서 연산이 더 쉬워집니다. 더 많은 뉴런이 있는 합성곱은 더 많은 커널 (kernel)에 걸쳐 퍼질 수 있습니다.
- 깊이는 그 반대로 더 순서적(sequential)입니다. 그래서 넓이를 늘리는 것이 계산적으로 더 효율적입니다.
- 여기서 이 연구가 넓이와 깊이와 중복 연결의 영향을 이해하려고 하길 시작했다는 것을 알 수 있습니다.
Aggregated Residual Transformations for Deep
Neural Networks(ResNeXt)
- 중복 블록 내에서, 여러 개의 병렬 경로가 있습니다. 그걸 비교적 더 날씬하게 해서, 병렬된 여러 개의 레즈넷을 갖는 것입니다.
Deep Networks with Stochastic Depth(확률적 깊이)
- 확률적 깊이(Stochastic Depth)는 깊이 문제를 더 들여다 보자!는 것이었습니다.
- 일단 더 깊이 더 깊이 들어가면, 전형적인 문제는 경사가 사라지는 vanishing gradient입니다.
- 경사를 긴 계층을 따라서, 즉 많은 수의 계층을 따라서 역전파하면 점점 더 작아질거고 결국 사라집니다.
- 그래서 훈련 동안에는 망을 짧게 하자는 것이었고, 계층의 하위 집합을 없애는 dropout 아이디어를 사용했습니다.
- 계층의 하위집합(subset)에 대해서 가중치를 드랍아웃(dropout) 하고 그것을 항등 연결(identity connection)로 설정했습니다.
- 그러면 훈련하는 동안 더 짧은 망들을 갖게 되고, 경사를 더 잘 역전파할 수 있습니다.

Beyond ResNets(ResNets 넘어서기)

FractalNet: Ultra-Deep Neural Networks without Residuals
- 프랙탈넷(FractalNet)에서 핵심은 얕은 망에서 깊은 망으로 효율적으로 전이(transitioning)하는 것이라고 생각합니다.
- 훈련 시킬때 하위 경로를 드랍아웃 하면서 합니다. 매우 좋은 성능을 보여줬습니다.
DenseNet: Densely Connected Convolutional Networks(밀도 높게 연결된 합성곱 망)
- dense block(덴스 블록)이라고 불리는 블록들이 있습니다. 각 블록에서 각 계층은 그 다음 각각의 다른 계층에 연결(feedforward)됩니다.
- 이 각각의 블록에 대한 입력은 또한 다른 각각의 conv(콘브) 계층의 입력이 되고 각각의 conv(콘브) 출력을 계산하면, 그 출력들은 이제 모든 계층으로 연결됩니다.
- 그후에, 이것들은 모두 conv(콘브) 계층의 입력으로 연결되고 그것들은 다른 과정을 거쳐서 차원을 줄이고 효율적이게 됩니다.
- 이것은 경사가 사라지는 문제를 완화합니다. 왜냐하면 밀도 높은 연결을 가지고 있기 때문입니다.
- 그건 피쳐 전파(propagation)를 강화하고 또한 피쳐 재사용을 권장합니다.
- 왜냐하면 매우 많은 이런 연결들이 있고 학습하고 있는 각 피쳐 지도들(feature maps)은 나중에 여러 계층에서 입력이 되고 여러번 사용되기 때문입니다.

Efficient networks(효율적인 망들)

SqueezeNet: AlexNet-level Accuracy With 50x Fewer
Parameters and <0.5Mb Model Size
- fire module이라고 불리는 것을 가지고 있는데, 그것은 많은 1 x 1 필터로 하나의 스퀴즈(squeeze) 계층을 구성하고 이후에 이것은 1 x 1과 3 x 3 필터가 있는 익스팬드(expand) 계층으로 들어갑니다(feed).
- 이미지넷에 대해 알렉스넷 수준의 정확도를 50배나 적은 파라미터로 얻을 수 있습니다.
- 더 심화된 망 압축을 해서 알렉스넷보다 500배 더 작게 할 수 있고 전체 망을 0.5MB로 만들수 있습니다.
- 이것은 우리가 어떻게 효율적인 망 모델 압축을 가질 수 있는지에 대한 방향을 알려줍니다.