1) ResNet 논문의 문제의식
서론(Introduction)을 통해 ResNet 논문이 제기하고 있는 문제의 핵심을 명확히 정리해 봅시다. 최초로 제기하는 질문은 딥러닝 모델의 레이어를 깊이 쌓으면 항상 성능이 좋아지는가 하는 것입니다. 그러나 이 질문이 문제의 핵심은 아닙니다. 레이어를 깊이 쌓았을 때 Vanishing/Exploding Gradient 문제가 발생하여 모델의 수렴을 방해하는 문제가 생기는데, 여기에 대해서는 이미 몇 가지 대응 방법이 알려져 있기 때문입니다.
가장 눈에 띄는 키워드는 바로 Degradation Problem이라는 표현입니다. 이것은 모델의 수렴을 방해하는 Vanishing/Exploding Gradient 문제와는 달리, 레이어를 깊이 쌓았을 때 모델이 수렴하고 있음에도 불구하고 발생하는 문제입니다. Introduction에서 제시된 아래 그래프가 이 문제의 핵심을 잘 보여줍니다.
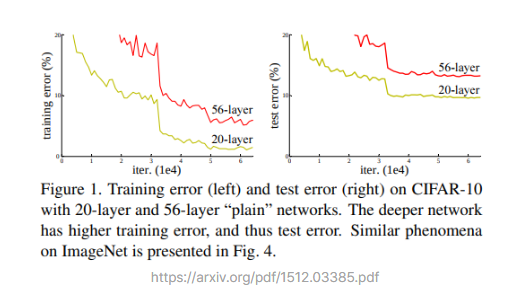
Q2. Introduction에서 Vanishing/Exploding Gradient 문제의 해결책으로 언급된 방법에는 어떤 것이 있나요?
normalized intialization, intermediate normalizaion layers
Q3.Degradation Problem이란 어떤 현상을 말하나요? Intoduction을 상세히 읽어본 후 자신의 표현으로 정리해봅시다.
**딥러닝 모델의 레이어가 깊어졌을 때 모델이 수렴했음에도 불구하고 오히려 레이어 개수가 적을 때보다 모델의 training/test error가 더 커지는 현상이 발생하는데, 이것은 오버피팅 때문이 아니라 네트워크 구조상 레이어를 깊이 쌓았을 때 최적화가 잘 안되기 때문에 발생하는 문제이다.
2) ResNet 논문이 제시한 솔루션: Residual Block
ResNet은 깊은 네트워크의 학습이 어려운 점을 해결하기 위해서 레이어의 입력값을 활용하여 레이어가 "residual function"(잔차 함수)을ㄹ 학습하도록 합니다.
위 문구는 논문 초록의 설명을 개락적으로 번역한 말이라 어렵게 들리실 수 있을 것 같습니다. 단순히 말하자면 일종의 지름길("shortcut connection")을 통해서 레이어가 입력값을 직접 참조하도록 레이어를 변경했다고 보시면 됩니다. Shortcut connectiond은 앞에서 입력으로 들어온 값을 네트워크의 출력층에 곧바로 더해줍니다. 네트워크는 출력값에서 원본 입력을 제외한 잔차(residual) 함수를 학습하기 때문에 네트워크가 ResNet이라는 이름을 가지게 되었습니다.
레이어를 많이 쌓았다고 해서 모델 성능이 떨어지는 것을 어떻게 설명해야 할까요? 저자들은 이 부분에 의문을 품었습니다. 만약 기존 모델에다가 identity mapping 레이어를 수십 장 덧붙인다고 해서 모델 성능이 떨어질 리는 없을 텐데, 그렇다면 레이어를 많이 쌓았을 때 이 레이어들은 오히려 identity mapping 레이어보다도 못하다는 뜻이 됩니다. 많이 겹쳐 쌓은 레이어가 제대로 학습이 이루어지지 않았다는 반증이 됩니다.
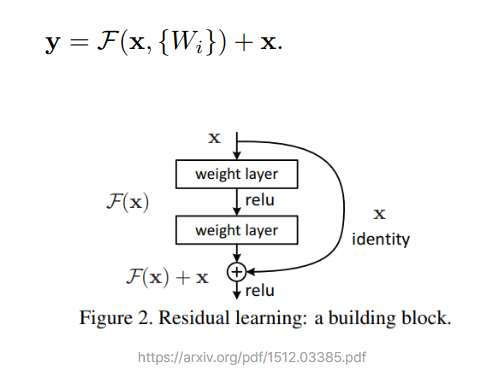
여기서 저자들이 기발한 생각을 합니다. 학습해야 할 레이어 H(x)를 F(x)+x로 만들면 어떨까? 여기서 x는 레이어의 입력값입니다. 그렇다면 설령 F(x)+x로 만들면 어떨까? 여기서 x는 레이어의 입력값입니다. 그렇다면 설령 F(x)가 Vanishing Gradient현상으로 전혀 학습이 안되어 zero mapping이 될지라도, 최종 H(x)는 최소한 identity mapping이라도 될 테니 성능 저하는 발생하지 않게 된다는 것입니다. 그렇다면 실제로 학습해야 할 F(x)는 학습해야 할 레이어 H(x)에다 입력값 x를 뺀 형태, 즉 잔차(residual) 함수가 되는데, 이것은 H(x)를 직접 학습하는 것보다는 훨씬 학습이 쉽지 않겠냐는 것입니다. 레이어를 깊이 쌓을수록 Residual에 해당하는 F(x)는 0에 가까운 작은 값으로 수렴해도 충분하기 때문입니다. 그리고 실험해 보니 이 구조가 실제로도 안정적으로 학습이 되며, 레이어를 깊이 쌓을수록 성능이 향상되는 것이 확인되었기 때문입니다.
정리하자면, Residual 레이어를 F(x)로 표현하면 이 레이어의 결과는 입력값 x에 대해 F(x)가 됩니다. 여기에 레이어의 입력값 x을 더해주면 최종 출력값은 F(x)가 됩니다. 여기에 레이어의 입력값 x을 더해주면 최종 출력값은 F(x)+x, 즉 우리가 보통 생각하는 레이어의 결괏값이 되겠지요. 이후 이 값은 ReLU 활성함수(activation function)을 거치게 됩니다. 위 식에서 F(x, Wi)는 학습되어야 할 residual mapping으로서 잔차 학습(residual learning)은 이 식을 학습합니다. ResNet에서는 shortcut connenction을 가진 ResNet의 기본 블록을 Residual Block이라고 부릅니다. ResNet은 이러한 Residual Block 여러 개로 이루어집니다.
이러한 shortcut connection의 아이디어는 다양한 레이어에 적용 가능하기 때문에 이후 나온 여러 네트워크 아키텍처에서 활용됩니다.
? 블록(block)이란 무엇인가요?
딥러닝 모델은 말 그대로 "깊기" 때문에, 깊은 네트워크를 쌓는 과정에서 레이어를 쌓는 패턴이 반복되기도 합니다. 반복되는 레이어 구조를 묶고, 각 구조 속에서 조금씩 바뀌는 부분은 변수로 조정할 수 있게끔 만드면 레이어 구조를 바꾸며 실험을 할 때에도 편리할 것입니다. 레이어를 묶은 모듈을 "블록"이라고 부르며, 일반적으로 조금씩 변형을 준 블록을 반복적으로 쌓아 딥러닝 모델을 만듭니다.
3) Experiments
간략히 살펴보셨다시피 딥러닝 논문에서는 모델의 설계를 설명한 뒤 모델을 실제로 구현해 그 효과를 입증합니다. ResNet을 예시로 논문의 실험(experiments) 부분을 조금 더 자세히 살펴봅시다.
ResNet에 추가된 shortcut connection의 아이디어를 검증하려면 어떤 실험을 해야 할까요? 당연히 shortcut connection이 없는 네트워크와 이를 사용한 네트워크를 가지고 성능을 비교해 봐야 할 것입니다.
실제 논문에서는 네트워크가 깊어짐에 따라 발생하는 경사소실(vanishing gradient) 문제를 ResNet이 해결함을 보여주기 위해서, shortcut connection의 유무와 네트워크 깊이에 따라 경우를 나누어 모델을 구현합니다. 18개 층과 34개 층을 갖는 네트워크를, 각각 shortcut이 없는 일반 네트워크(plain network)와 shortcut이 있는 ResNet 두 가지로 구현해 총 4가지를 만든 것이지요. 이후 이미지넷(ImageNet) 데이터를 사용해 각 모델을 훈련을 시킨 뒤 효과를 분석합니다.
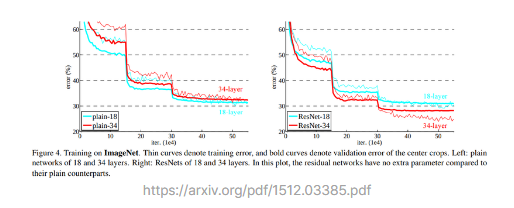
위 그림에서 왼쪽은 일반 네트워크 두 개로 네트워크가 깊어지더라도 학습이 잘되지 않는 것을 볼 수 있습니다. 34개 층을 갖는 네트워크가 18개 층을 갖는 네트워크보다 오류율(error rate)이 높지요. 하지만 shortcut이 적용된 오른쪽에서는 레이어가 깊어져도 학습이 잘 되는 효과를 볼 수 있습니다. 그렇다면 이렇게 학습된 모델은 검증 데이터셋(vallidation dataset)에서 어떻게 차이가 날까요?
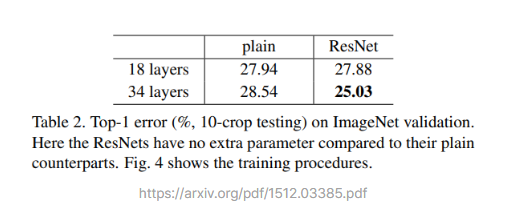
위 표는 이미지넷 검증 데이터셋을 사용해 실험한 결과를 나타냅니다. Top-1 error란 모델이 가장 높은 확률 값으로 예측한 class 1개가 정답과 일치하는지 보는 경우의 오류율입니다. Top-5는 모델이 예측한 값들 중 가장 높은 확률 값부터 순서대로 5개 class 중 정답이 있는지를 보는 것이지요. 이 숫자는 당연히 낮을수록 좋습니다.
일반 네트워크는 레이어가 16개나 늘어나 네트워크가 깊어졌는데도 오류율은 오히려 높아졌습니다 .경사소실로 인해 훈련이 잘되지 않았기 때문입니다. ResNet에서 잘 훈련된 레이어가 16개가 늘어난 효과로 오류율이 2.85% 감소했습니다. 논문에서는 이렇게 간단한 실험으로 Residual Block의 효과를 입증하고 있습니다.
Q4. 어떤 태스크(task)의 모델 간 성능을 비교할 때 널리 사용되어 기준이 되는 데이터셋을 벤치마크 데이터셋이라고 합니다. 이를 통해서 최첨단 성능, 즉 State of the atr(SOTA)을 기록하는 모델을 가리기도 하는데요. 논문의 실험에서는 ResNet에 앙상블(ensemble)을 적용한 모델과 다른 앙상블 모델을 비교한 표를 제시합니다. 이 실험에서 ResNet 앙상블의 분류(classification) 태스크 Top-5 error는 얼마였나요? 논문에서 찾아보세요.
3.57를 기록했습니다.