[ML]Neural ODE

ball·2024년 5월 29일
ML

Summary

It is surprising that Neural ODE can express an differential equation.
I wanna talk about how we can solve the IVP(Initial Value Problem) using Neural Network.

IVP(Initial Value Problem)

IVP is a famous problem in calculus.

h(T)=h(0)+∫0Tdh(t)dtdth(T) = h(0) + \int_{0}^{T}\frac{dh(t)}{dt}dt

If the h(0)h(0) and dh(t)dt\frac{dh(t)}{dt} is given, then we can calculate the integral and get h(T).

However, computers cannot do the integral operation. We need an algorithm that can make computers calculate the approximate solution of IVP.

Euler Discretization

Given a IVP

h(T)=h(0)+∫0Tdh(t)dtdth(T) = h(0) + \int_{0}^{T}\frac{dh(t)}{dt}dt

Let's discretize with step size s≈0s\approx 0

f(h(t))=dh(t)dtf(h(t)) = \frac{dh(t)}{dt}
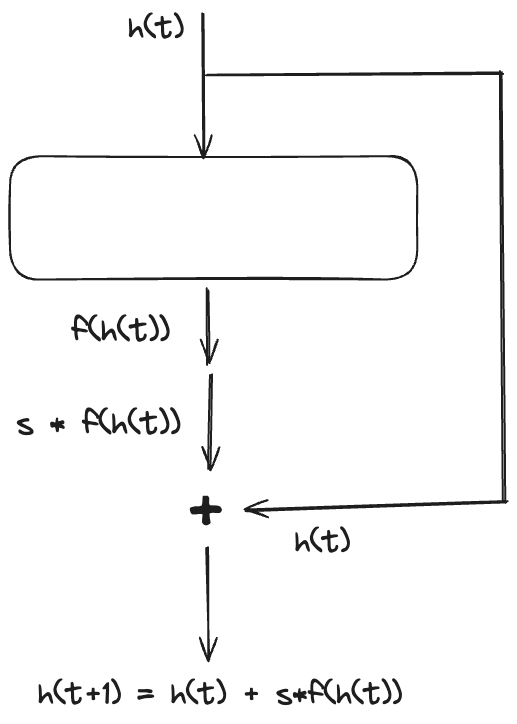
h(t+s)=h(t)+s⋅f(h(t))h(t+2s)=h(t)+s⋅f(h(t+s))...h(T)=h(T−s)+s⋅f(h(T−s))h(t+s) = h(t) + s\cdot f(h(t)) \\ h(t+2s) = h(t) + s\cdot f(h(t+s)) \\ ...\\ h(T) = h(T-s) + s\cdot f(h(T-s))

Given h(t)h(t) and f(h(t))f(h(t)), evaluating h(T)h(T) is a forward problem.

Given data h(x1),h(x2),...h(xn)h(x_1), h(x_2), ... h(x_n), getting f(h(t))f(h(t)) is a backword problem.

Euler Discretization with ResNet

It is surprising that Euler Discretization algorithm can be implemented by ResNet. Following image is part of ResNet. We can see the Euler Discretization algorithm can be expressed with ResNet.

Alternative ODE-Solver

Euler Discretization is a very simple(and powerful) algorithm for solving IVP. There are many other ODE-Solver such as Runge-Kutta Method or DOPRI Method. They are all based on Euler Discretization method. It just have more calculation to make it accurate.
In DOPRI Method, it's step size changes depending on the slope of h(t)h(t).

Training Neural ODE

We can train the Neural ODE(ResNet) using Normal Backpropagation of ResNet. However, we have a problem.
Assume the total # of steps in DOPRI-Solver is 10,000. If we use Normal Backpropagation Method, we need 10,000 Layers. But this is impossible. Recent research use severel hundreds of layer, and it already requires massive amount of computation for backpropagation.

We need a alternative method for training Neural ODE.

Normal Backpropagation Method

Let's see how it will be trained if we apply normal backpropagation method to Neural ODE.
∂L∂zT\frac{\partial L}{\partial z_{T}} is known. zTz_T is the last layer output.
Let's say the step size is h≈0h\approx0
Let's define at=∂L∂zta_t = \frac{\partial L}{\partial z_t}.

zt+h=zt+h⋅f(zt)z_{t+h} = z_t + h\cdot f(z_t)

∂L∂zt=∂L∂zt+h⋅∂zt+hzt\frac{\partial L}{\partial z_{t}} = \frac{\partial L}{\partial z_{t+h}}\cdot \frac{\partial z_{t+h}}{z_t}
=∂L∂zt+h⋅{1+h⋅∂f(zt)∂zt}= \frac{\partial L}{\partial z_{t+h}}\cdot \left\{1+h\cdot\frac{\partial f(z_t)}{\partial z_t} \right\}
=at+h⋅{1+h⋅∂f(zt)∂zt}= a_{t+h} \cdot \left\{1+h\cdot\frac{\partial f(z_t)}{\partial z_t} \right\}

Using the upper equation, we can get the gradient of the layer that outputs ztz_t.

∂L∂θt=∂L∂zt+h⋅∂zt+h∂θt\frac{\partial L}{\partial \theta_t} = \frac{\partial L}{\partial z_{t+h}} \cdot \frac{\partial z_{t+h}}{\partial \theta_t}

Then we can derive

∂L∂θt=at+h⋅∂(zt+h⋅f(zt))∂θt=at+h⋅h⋅∂f(zt)∂θt\frac{\partial L}{\partial \theta_t} = a_{t+h} \cdot \frac {\partial (z_t + h \cdot f(z_t))}{\partial \theta_t} = a_{t+h} \cdot h \cdot \frac {\partial f(z_t)} {\partial \theta_t}

This means that we need a layer for every steps. This requires huge amount of calculation. We have to think of more better option.

Adjoint Sensitivity Method

Let's go through a simple equation of getting value of z(t+h)z(t+h).

z(t+h)=z(t)+∫tt+hf(z(t′))dt′z(t+h) = z(t) + \int_{t}^{t+h}f(z(t'))dt'

This is the start of adjoint method.
Now let's define a(t)=∂L∂z(t)a(t) = \frac{\partial L}{\partial z(t)}.

a(t)=∂L∂z(t)a(t) = \frac{\partial L}{\partial z(t)}
=∂L∂z(t+h)⋅∂z(t+h)∂z(t)= \frac{\partial L}{\partial z(t+h)} \cdot \frac{\partial z(t+h)}{\partial z(t)}
=a(t+h)⋅{1+∂∫tt+hf(z(t′))dt′∂z(t)}= a(t+h) \cdot \left\{ {1 + \frac{\partial \int_{t}^{t+h}f(z(t'))dt'}{\partial z(t)}}\right\}

Using adjoint method, we can easily calculate the ata_t using da(t)dt\frac{da(t)}{dt}.

da(t)dt=lim⁡h→0+a(t+ε)−a(t)ε\frac{da(t)}{dt}= \displaystyle \lim_{h \to 0+} \frac{a(t+\varepsilon) - a(t)}{\varepsilon }
=lim⁡ε→0+a(t+ε)−a(t+ε){1+∂∫tt+εf(z(t′))dt′∂z(t)}ε= \displaystyle \lim_{\varepsilon \to 0+} \frac{a(t+\varepsilon) - a(t+\varepsilon) \left\{ {1 + \frac{\partial \int_{t}^{t+\varepsilon}f(z(t'))dt'}{\partial z(t)}}\right\} }{\varepsilon }

Using the following equation,

∫tt+εf(z(t′))dt′=∫tt+ε∂z(t′)∂t′dt′=z(t+ε)−z(t)\int_{t}^{t+\varepsilon}f(z(t'))dt' = \int_{t}^{t+\varepsilon} \frac {\partial z(t')} {\partial t'} dt' = z(t+\varepsilon) - z(t)

We can derive the following equation.

da(t)dt=lim⁡ε→0+−a(t+ε)⋅∂f(z(t))∂z(t)=−a(t)⋅∂f(z(t))∂z(t)\frac {da(t)}{dt} = \displaystyle \lim_{\varepsilon \to 0+} -a(t+\varepsilon) \cdot \frac {\partial f(z(t))} {\partial z(t)} = -a(t) \cdot \frac {\partial f(z(t))} {\partial z(t)}

Using da(t)dt\frac {da(t)} {dt} and a(T)a(T), we can calculate a(t′)a(t') for any t′t'.
We can apply this to the Normal backpropagation method with less layers. We don't need a layer for every step.

∂L∂θt=at+h⋅∂(zt+h⋅f(zt))∂θt=at+h⋅h⋅∂f(zt)∂θt\frac{\partial L}{\partial \theta_t} = a_{t+h} \cdot \frac {\partial (z_t + h \cdot f(z_t))}{\partial \theta_t} = a_{t+h} \cdot h \cdot \frac {\partial f(z_t)} {\partial \theta_t}

Summary

I was surprised that we can solve differential equation using ResNet. Machine Learning is integrated into many areas such as physics and mathematics.

profile
ball
KAIST CS Major
이전 포스트

velog 블로그를 시작하며

다음 포스트

[ML] Fourier Feature Encoding

0개의 댓글