230710 Today I Learned

오늘 TIL은 개념만 알고 있었던 꼬리재귀에 대해 정리해보려 한다.

---

---

재귀(Recursion)

함수가 자기 자신을 호출하는 것.

• 정렬 알고리즘을 하면서 여러 재귀 함수를 겪었다. 분할정복 방법이 특히 재귀적으로 자기자신을 호출하는 형태를 가졌다.

• 예시 : 병합 정렬 알고리즘 안에서의 재귀

...
  private static void mergeSort(int[] array, int left, int right){
    if (left >= right) return;

    int mid = (left + right) / 2;

    mergeSort(array, left, mid);          // left~mid까지 자기 자신을 재귀로 호출
    mergeSort(array, mid+1, right); // mid+1~right까지 자기 자신을 재귀로 호출
    
    merge(array, left, mid, right);       // 분할된 배열을 병합
  }
...

• 재귀는 주어진 문제를 더 작은 하위문제로 분할하고 각 하위문제를 해결하기 위해 자기자신을 호출한다.

• 종료 조건이 충족될 때까지 자기자신을 호출하면서 작업을 수행한다.

• 팩토리얼, 순열, 수열, 분할정복 알고리즘, DFS, BFS에서 재귀가 사용된다.

• 장점 : 코드가 간결하고 가독성이 좋다.
  복잡한 문제를 간단하고 이해하기 쉽게 표현할 수 있다.

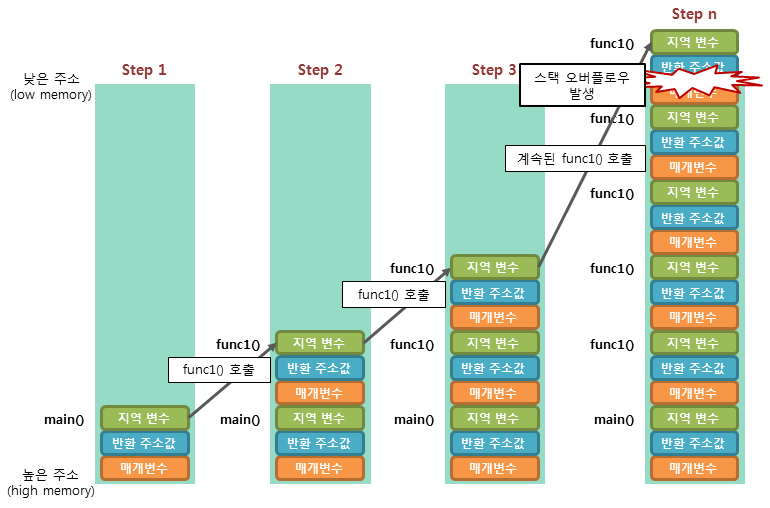
이미지 출처 : tcp school

• 단점 : Stack Overflow. 스택 메모리상에서 재귀함수가 자기 자신의 실행도 마무리 하지 않고 반복적으로 자기 자신을 호출한다면 스택 메모리의 한계에 도달해 Stack Overflow 문제가 발생할 수 있다.
  자기 자신 호출에 따른 오버헤드 발생으로 인한 성능저하가 있다.
  디버깅이 복잡하다.

---

꼬리 재귀(Tail Recursion)

재귀 호출이 함수의 가장 마지막 작업으로 수행되는 것.
즉, 재귀 호출 이후 추가적인 연산이 없도록 구현하는 것.

• 재귀의 장점은 살리고 단점은 보완하는 방법이다.

• 재귀함수의 Stack Overflow를 해결를 해결하기 위해 고안되었다.

• 재귀함수의 실행 결과가 연산에 사용되지 않고 바로 반환되게 함으로써 이전 함수의 상태를 유지할 필요가 없도록 하는 방식이다.

• 꼬리재귀를 사용하면 함수 호출이 반복되어 스택이 깊어지는 문제를 컴파일러가 일반적인 반복문처럼 취급하도록 최적화를 수행한다. 더이상 값이 변할 여지가 없으므로 기존 스택 프레임을 재사용할 수 있어 아무리 많은 재귀호출을 하더라도 Stack Overflow 문제를 해결한다.

• 이로인해 스택 메모리 사용량이 줄어들고, 함수 호출에 따른 오버헤드가 줄어 프로그램의 성능이

• 하지만 꼬리재귀가 동작하려면 프로그래밍 언어(혹은 컴파일러)가 TCO(Tail Call Optimization)을 지원해야한다.
  Scheme이나 Haskell, 일부 버전의 JavaScript이 이를 지원한다.

꼬리재귀 in Java

자바(+파이썬)는 꼬리재귀 최적화 TCO를 직접적으로 지원하지 않는다. 꼬리재귀 방식으로 직접 함수를 구현할 수는 있지만 꼬리재귀 최적화를 지원하지 않아 호출 스택을 절약하진 못하며 이렇게 구현해도 Stack Overflow를 피하진 못한다. 그래서 자바에서는 반복문을 사용하는 것이 일반적이다.

• jdk 클래스의 보안에 민감한 일부 메서드는 메서드 호출을 누가 했는지 알아내기 위해 jdk 라이브러리 코드와 호출 코드간의 스택 프레임 개수에 의존한다. TCO로 인한 스택 프레임 수 변경이 생기면 이 의존관계가 망가져 에러가 발생할 수 있다.

• Java 컴파일러가 직접 TCO를 지원하진 않지만, java 8 이후 추가된 람다와 함수형 인터페이스로 꼬리재귀와 같은 컨셉을 적용할 수는 있다고 한다. 이부분에 대해선 추후 새로운 TIL로 공부해보려 한다.

• 해당 내용 출처 : dldhk97.log

팩토리얼 예시

자바의 문법을 사용해 예시를 들긴 했지만 자바로는 아래와 같은 방법으로는 불가능하다. 일단 논리만 보자.

• 일반 재귀 함수로 구현한 팩토리얼

// 재귀 팩토리얼
int factorial(int n) {
    if (n > 1) {
        return n * factorial(n - 1); // 반환부에 연산이 존재함
    } else {
        return 1; // 정지 조건
    }
}

재귀함수로 팩토리얼을 구현했을 때, 반환부를 보면 'factorial(n - 1)'의 호출이 먼저 이루어지고 n과 곱해져 반환된다. 반환부에서 곱하기 n이라는 추가적인 연산이 남아있기 때문에 자기 자리를 기억하고 있어야 하고, factorial(n)의 스택을 닫지 못한 채로 factorial(n - 1)의 스택을 열어야만한다.
값을 받으면 그 값에 연산을 하고 다른 함수에게 전달하는 것이다.
반복적으로 호출이 쌓이다가 스택 한계에 도달하면 Stack Overflow 문제가 하게 된다.

• 꼬리재귀로 구현한 팩토리얼

// 꼬리 재귀 팩토리얼
int accumulator = 1;

int factorial(int n, int accumulator) {
    if (n > 1) {
        return factorial(n - 1, n * accumulator);
    } else {
        return accumulator;
    }
}

(TCO를 지원하는 언어에서는) 위의 일반 재귀함수와 다르게 반환부에서 '곱하기 n' 같은 추가적인 연산이 없다. 따라서 각 함수들은 아무 연산도 하지 않고 accumulator 변수를 통해 값을 전달만 한다. 아무런 연산이 남아있지 않기 때문에 자기 자리를 기억하지 않아도 되고, 스택에 위치값을 저장할 필요도 없다. 따라서 새로운 스택 프레임을 생성하지 않고 기존 스택 프레임을 재사용해 매개 변수 값만 갱신해서 사용한다.