Today I Learned
오늘은 tensor의 생성과 조작에 대해 공부했다.
강의 복습
Tensor 모양 변경
-
크기에 -1을 넣으면 알아서 나머지 계산해서 넣어준다.
-
view()
Tensor가 연속적으로 메모리 할당되었을 때(slicing으로 비연속적이면 안됨, 메모리 연속할당은 .is_continuous()로 확인 가능)
reshape()에 비해 성능이 좋다.
view(1,2,3) 처럼 원소수는 그대로 두고 tensor의 차원(모양)을 변경할 수 있다. -
flatten()
차원을 평탄화 시킨다. 파라미터가 없으면 1차원으로 평탄화한다.
a = x.flatten(start_dim=1, end_dim=2) 처럼 시작과 끝 차원 지정이 가능하다. -
reshape()
view랑 다르게 메모리 연속 할당이 아니어도 쓸 수 있다.(다만 성능은 view보다 별로) -
transpose(a,b)
a,b차원의 축을 서로 바꾼다. -
squeeze()
텐서의 크기가 1인 차원을 제거한다. -
unsqueeze(input, dim)
input을 지정된 dim 위치에 차원을 넣는다. -
stack(tensors, dim=0, *, out=None) -> Tensor
새로운 차원을 추가하여 텐서를 쌓는다.(모두 같은 크기여야 함) -
cat(tensors, dim=0, *, out=None) -> Tensor
기존 차원을 따라 텐서를 연결한다.(주어진 차원을 제외한 모든 차원이 동일해야함) -
expand(*sizes) -> Tensor
메모리 할당 없이텐서를 확장한다.(확장할 차원의 크기가 1이어야 한다) -
repeat(*sizes) -> Tensor
텐서를반복해 새로운 텐서를 만든다.(새로 메모리 할당)
Tensor 기초 연산
in-place 연산
새로운 메모리 할당 없이 첫번째 입력 텐서에 결과 값을 저장하는 연산
각 산술연산 함수 뒤에_을 넣으면 된다.
다만 호환성 문제가 발생할 수 있으니 주의해서 사용!
ex) x.add(y), x.sub(y), t1.mul(t2), t.pow(n)
산술연산
-
torch.add(x,y)
x와 y 텐서에서 위치가 같은 요소들을 더해서 반환한다.
텐서들끼리 차원은 같지만 크기가 다르면 브로드캐스팅 규칙을 적용해 더한다.(numpy와 유사)
입력 텐서들의 값을 변경하지 않고, 결과를 새로운 텐서에 저장해 추가적인 메모리를 사용한다 -
뺄셈은 torch.sub(x,y), x.sub_(y)로 위와 같이 할 수 있다.
-
torch.mul(scalar,t)
스칼라곱. 텐서에 동일한 스칼라를 곱하는 연산 -
torch.mul(t1,t2)
크기가 동일한 두 텐서의 같은 요소끼리 곱셈.
크기가 다르면 덧셈처럼 브로드캐스팅 규칙 적용 -
torch.div(t1,t2)
t1의 각 요소를 위치가 맞는 t2의 각 요소로 나눈다. -
torch.pow(t,n)
t텐서의 각 요소를 n제곱
n자리에 1/n을 넣으면 거듭제곱근 연산 가능
비교연산
torch.gt(t1,t2) 모양에서 t1의 요소를 t2의 요소와 비교하는 연산들
크기가 같아야 하고 결과는 boolean 텐서로 출력해준다.
같다 = eq / 다르다 = ne / 크다 = gt / 작다 = lt / 크거나같다 = ge / 작거나 같다 = le
논리연산
torch.logical_and(t1,t2)
and자리에 or, xor을 넣어 연산이 가능하다.
결과값은 boolean 텐서로 출력된다.
행렬(matrix) 곱셈
그냥 각 요소를 곱하는 것과는 다르다. 두 행렬을 결합해 새로운 행렬을 생성한다.
흑백 이미지의 좌우 or 상하 대칭이동이 행렬 곱셈으로 가능하다.
x.matmul(y) or x.mm(y) or x @ y
Norm
vector나 행렬의 크기를 측정할때 사용되는 수학적 개념
얼마나 원점에서 떨어져있는지를 의미한다.
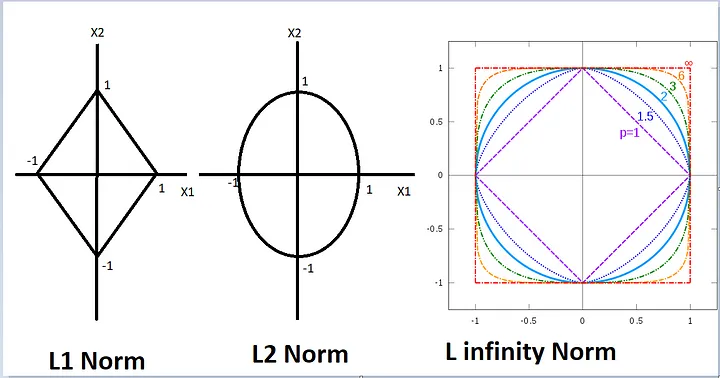
이미지 출처 : Satishkumar Moparthi
| 노름 종류 | PyTorch 함수 | 설명 |
|---|---|---|
| L1 노름 (맨해튼 노름) | torch.norm(t, p=1) | 요소들의 절대값의 합 |
| L2 노름 (유클리드 노름) | torch.norm(t, p=2) | 요소들을 제곱해 더한 값의 제곱근 |
| L∞ 노름 | torch.norm(t, p=float('inf')) | 요소들의 절대값 중 최대값 |
- torch.norm(A) 라고만 하면 pytorch에선 디폴트 값은 L2노름이다!
유사도(similarity)
두 개체(벡터, 행렬, 이미지 등)간 유사성을 측정하는 지표
각 유사도는 1에 가까울 수록 유사하다고 판단한다.
-
맨해튼 유사도
두 벡터사이의 맨해튼 거리를 역수로 변환한 값
각 요소간 차이의 합을 맨해튼 거리라고 하고1/(1+맨해튼거리)가 맨해튼 유사도
1/(1+torch.norm(a-b,p=1)) -
유클리드 유사도
두 벡터 사이의 유클리드 거리를 역수로 변환한 값
각 요소간 차이의 제곱합의 제곱근이 유클리드 거리고,1/(1+유클리드거리)가 유클리드 유사도
1/(1+torch.norm(a-b,p=2))
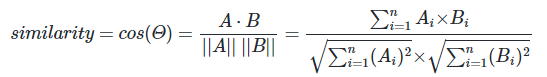
- 코사인 유사도
두 벡터 사이의 각도를 측정해 계산한 값. -1~1의 범위를 가진다.
코사인 유사도는 내적(두 벡터의 관계를 하나의 스칼라로 변환. 각 요소끼리 곱해서 더함)을 통해서 구한다.
두 벡터간 내적을 구해서 각 벡터의 L2노름의 곱으로 나눠주면 코사인유사도를 구할 수 있다.
# 코사인 유사도 직접 계산하는 방법
A = torch.tensor([1.0, 2.0, 3.0])
B = torch.tensor([4.0, 5.0, 6.0])
dot_product = torch.dot(A, B)
norm_A = torch.norm(A)
norm_B = torch.norm(B)
cosine_similarity = dot_product / (norm_A * norm_B)
print(cosine_similarity) # tensor(0.9746)
과제 1
과제는 큰 문제없이 풀었다. 질문사항이 있거나 기록해 둘것은 목요일 팀 피어세션에서 진행해보자.
피어세션 정리
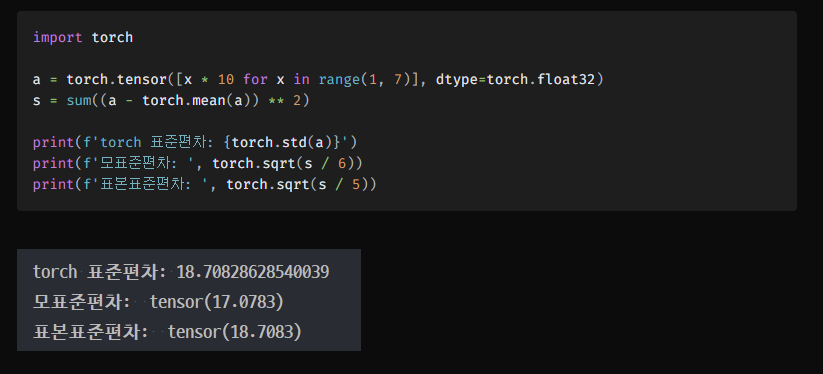
pytorch에서는 기본적으로 torch.std가 모표본편차가 아니라 표본표준편차 기준이다.
대부분은 표본이 기준이다.
3-d 이상의 텐서도 실무에서는 많이 쓰인다.
dimmension에 대한 이해가 약간 필요할 것 같다.
- 자료구조, 메모리에 대한 공부를 진행해야할 지 멘토링시간때 질문하기
통계 및 표준편차 참고 사이트 : 로스카츠의 AI 머신러닝
회고
-
과제 양이 생각보다 많아서 진도를 빨리 쳐내야 할 것 같다.
-
dimmension에 대해 직관적인 이해가 좀 떨어져서 좀 더 수련이 필요할 것 같다.
