Today I Learned
이번주는 ML LifeCycle에 대해서 배운다!
강의 복습
Machine Learning(ML)
컴퓨터가 명시적으로 프로그래밍되지 않고도 데이터를 통해 학습하고, 그 학습한 내용을 바탕으로 예측이나 결정을 내릴 수 있도록 하는 기술
-
작업(T)에 대해 경험(E)과 함꼐 성능(P)을 향상시키는 것 - Tom Mitchell
P : 결과 측정 지표, T : 수행해야하는 작업, E : 데이터셋 / PTE를 정의해야한다. -
AI > 머신러닝 > 딥러닝
-
데이터로부터 패턴을 찾고, 그 패턴을 기반으로 결과를 예측하는 패턴 인식 모델
ML 종류
-
지도학습(Supervised Learning)
입력 데이터와 그에 대응하는정답(lable)이 주어질 때, 모델이 입력과 출력 간의 관계를 학습하는 방식(귀납적 학습).
ex) 회귀 분석(Regression, y가 숫자), 이미지 분류(Classification, y가 카테고리) -
비지도 학습(Unsupervised Learning)
입력 데이터에는정답이 없고(학습데이터만), 모델이 데이터의 구조나 패턴을 학습하는 방식
ex) 군집화(Clustering), 차원 축소 -
강화 학습(Reinforcement Learning)
에이전트(ml 모델)가 환경과 상호작용하면서보상을 최대화하는 방향으로 스스로 학습하는 방식.
ex) 게임에서의 최적 전략 학습(Alpha Go), 자율주행.
ML LifeCycle
머신러닝 프로젝트를 효과적으로 계획, 개발, 배포, 유지 보수하는 데 필요한 일련의 단계
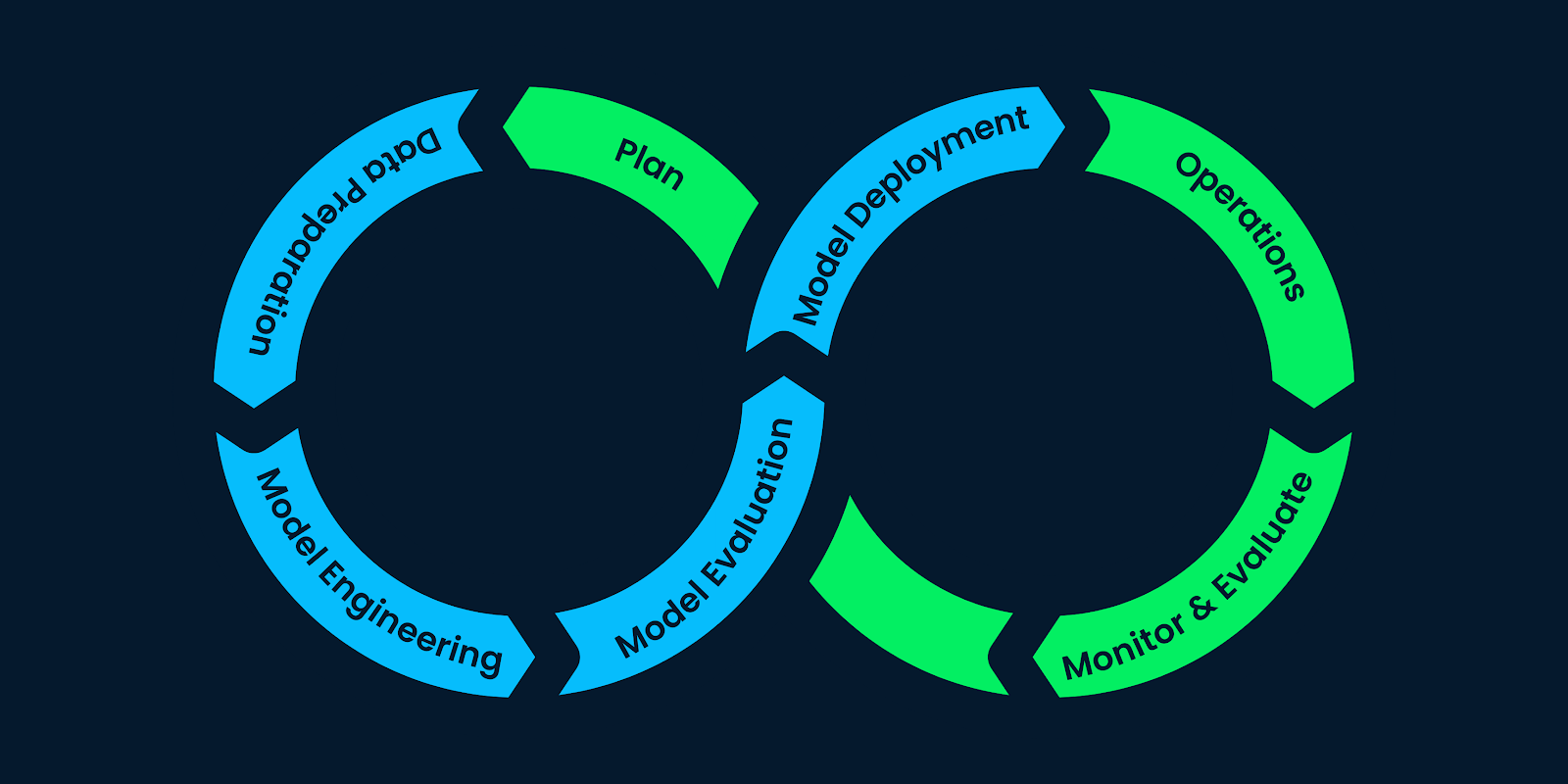이미지 출처 : datacamp
-
계획 - 데이터 준비 - 모델 엔지니어링 - 모델 평가 - 모델 배포 - 모니터링 / 유지 보수
-
계획 단계에서는 모델의 성능을 어떻게 평가할 것인지, 어떤 기준을 사용해 성공 여부를 판단할 것인지 목표를 세우고 평가 지표를 설정한다.
-
견고성(robustness)
모델이 이상치나 노이즈에 크게 영향을 받지 않는다.
학습 데이터에 과하게 over-fitting 되지 않았다. -
데이터 준비과정에서는 데이터 수집, labeling, cleaning(정제), 전처리 및 관리를 거친다.
선형대수
벡터와 행렬을 사용하여 선형 방정식, 벡터 공간, 변환 등을 연구하는 수학분야
-
회귀(Regression)
변수들 간의 관계를 모델링하여 하나의 종속 변수(목표 변수)를 하나 이상의 독립 변수(예측 변수)로 예측하는 통계 기법
-
회귀 분석(Regression Analysis)
입력 변수(input)와 출력 변수(output) 간의 수학적 관계를 추정하는 과정
특징변수, 독립변수, 설명변수, input, 원인, x
-> 목표변수, 종속변수, 응답변수, output, 결과, y
Linear Regression
종속 변수와 하나 이상의 독립 변수사이의 관계를
직선(선형 함수)으로 모델링하는 통계 기법
-
방정식 :
y = mx + b기울기 m과 절편 b -
다중 선형 회귀
input이 여러개인 선형회귀. 하나의 y값에 여러 x값이 걸려있다.
y = b0 + b1x1 + b2x2 + ... + bnxn
선형회귀의 가정
- 선형성
독립 변수와 종속 변수 사이에 선형 관계가 존재해야한다. - 독립성
관측 값과 잔차(오차의 추정치, 예측과 실제값의 차이, residual)들은 서로 독립적이어야 한다.
한 관측치의 오차가 다른 관측치의 오차에 영향을 주지 않아야 한다. - 등분산성
잔차의 분산이 일정해야 한다. - 정규성
잔차들은 정규 분포를 따라야 한다. 오차들이 평균이 0이고, 정규 분포를 따라야 한다.
최소제곱법(OLS)
선형 회귀 분석에서 가장 널리 사용되는 모델 최적화 방법
데이터 포인트와 회귀선 사이의 거리(잔차, residual)를 최소화하는 회귀 계수를 추정하는 방법
-
즉, 잔차의 제곱합을 최소화하는 방향으로 회귀선을 추정한다.
-
실제값 y에서 예측값 mx + b를 뺀 residual의 제곱합을 최소화 하는 m과 b를 구한다.
회귀 모델 평가 지표
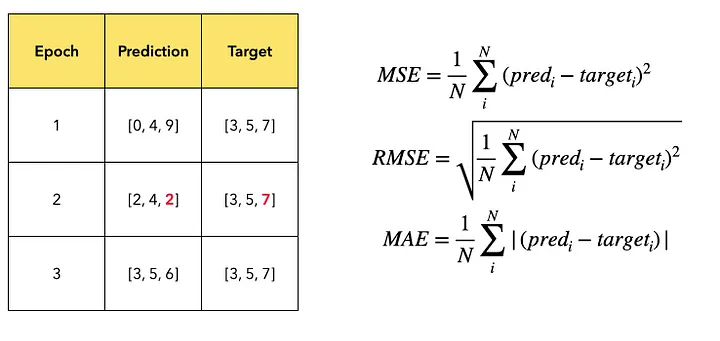이미지 출처 : medium - Jaeyoung Cheong
-
평균 절대 오차(MAE)
예측값과 실제값 간의 절대 오차의 평균 합.
직관적이고 간단하며 모든 오차를 동일하게 고려해 이상치에 robust하다.
그리고 단위가 종속변수와 같아 해석이 쉽다. -
평균 제곱 오차(MSE)
예측값과 실제값 간의 차이의 제곱을 평균 합.
큰 오차에 민감하게 반응해 모델의 큰 오차를 줄일 수 있지만, 이상치에 민감하다. -
평균 제곱근 오차(RMSE)
MSE의 제곱근. MSE의 장점을 가지면서 단위도 종속변수와 같다.
MSE처럼 큰 오차에 민감하게 만응한다. -
결정계수
R^2 = 1-(RSS/TSS)
RSS : 잔차 제곱합(실제값-예측), TSS : 총 제곱합(실제값-평균)
모델의 설명력을 평가하는 지표. 모델이 종속변수의 변동성을 얼마나 잘 설명하는지 나타낸다. 1에 가까울수록 예측값이 실제값과 일치하고, 0은 단순한 평균값과 비슷하며, 음수는 평균 사용하는 것보다 성능이 떨어짐을 의미한다.
Nearest Neighbor Classifier
주어진 데이터를 기반으로 새로운 데이터 포인트의 클래스를 예측하는 비모수(non-parametric) 분류 기법
가장 가까운 이웃(neighbors)의 정보를 사용하여 데이터 포인트의 클래스를 결정한다.
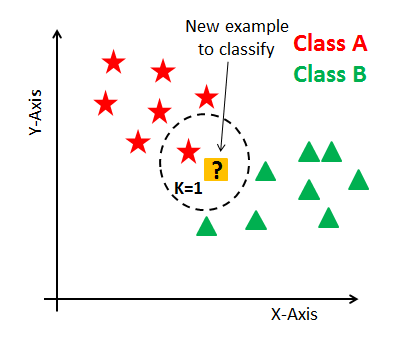이미지 출처 : atrium - Raushan Jha
-
k-NN 알고리즘
가장 가까운 k개의 neighbor 데이터 포인트를 찾아 예측한다.
일반적으로 k값을 홀수로 둬서 다수결 타당성을 높인다. -
NN Classifier는 train 학습과정에서는 모든 데이터와 라벨의 pair를 기억하는 것 말고는 하는게 없어 lazy method라고도 한다.
predict 과정에선 가장 유사한 훈련 예제의 라벨을 출력한다. -
복잡한 모델링과 훈련 과정이 필요하지 않고 훈련 데이터에 직접 의존한다(비모수적)
따라서 훈련은 간단한데 예측 과정에서 시간복잡도가 더 커지는 단점이 생긴다.
특히 차원이 커질수록 비용이 크게 증가한다. -
유사도를 측정하는 metric을 만들어야 하는 데 이 과정이 어렵다.
일반적으로 이미지 픽셀간 L1, L2 거리를 사용한다.
하지만, 이미지를 변형해도 L2거리는 같기 때문에 cv에선 nn을 잘 쓰지 않는다. -
결정 경계(Decision Boundary)
데이터 포인트가 어느 클래스에 속하는지를 결정하는 경계선, 기준.
k-nn에선 비선형 결정 경계를 형성하는데, 이 값은 k값에 따라 달라진다.
일반적으로 k가 커질수록 부드럽고 단순해지며, k가 작아지면 좀 더 local해져 데이터의 노이즈에 민감해진다.
Linear Classifier
입력 공간에서 선형 결정 경계를 기반으로 데이터를 분류하는 모수적(parametric) 기법
-
학습 데이터를 모두 저장할 필요가 없어 공간 효율적이며, Wx만 계산하면 되기 때문에 테스트시 NN보다 훨씬 빠르다.
-
이미지 x가 있으면 x와 같은 크기에 각 픽셀에 매핑되는 파라미터 w(가중치)를 계산한다.
y = w(1,1)x(1,1) + w(1,2)x(1,2) +... + w(m,n)x(m,n) + b -
ex) 이미지 x가 10x10x3 픽셀을 가지고 있고, 가질 수 있는 label이 10개(10x1)라면
f(x,w) = Wx + b는10x1 = (10x300)@(300x1) + 10x1의 크기여야된다.
이는 W'x' = (10x301)@(301x1)로 W'=[W b]의 행벡터, x' = [x 1]의 열벡터로 계산할 수도 있다. -
절편(편향) b는 input 데이터와 직접 상호작용하지 않으면서 output에 영향을 주기 때문에, 데이터의 분포나 본성과 관련있다.(데이터 자체에 의자 이미지가 많으면 의자 확률이 일단 높아지는 것)
Softmax Classifier
다중 클래스 분류 문제를 해결하기 위해 사용되는 선형 분류기
-
Linear 분류기의 결과 점수는 해석하기 어렵다. 이를 0~1 사이의 각 클래스에 속할 확률로 해석할 수 있게 변환한 것이 softmax classifier.
-
점수를 확률화 하려면 클래스가 2개일 때는 sigmoid를 적용하면 되자만, 다중 클래스 문제일 때는 이를 일반화해서 각각의 클래스가 될 확률로 계산하는데 이를 softmax라 한다.
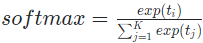
- 매개변수 값 정하는 과정
모델의 형식을 먼저 만들고 처음엔 매개변수(W)를 랜덤하게 만든다.
그리고 학습데이터를 통해 학습을 진행하면서 추정값과 실제 라벨을 비교해 loss가 얼마나 발생했는지 계산하고(손실함수), 이를 최소화하도록 매개변수(W)를 업데이트(최적화)해서 추정과 실제값이 일치될 때 까지 반복학습한다.
손실 함수
머신러닝 및 딥러닝 모델에서 모델의 예측과 실제 정답 사이의 차이를 측정하는 함수
-
모델의 성능을 평가하고, 모델을 훈련시키는 과정에서 가중치와 파라미터를 조정하는 데 사용된다.
-
회귀문제에선 MAE, MSE, RMSE 등을 사용한다.
-
차별적(discriminative) 설정에서 손실함수는 지수손실, 로그손실, 힌지손실 등이 있다.
-
확률적 설정에서 손실함수는 이진분류는 sigmoid, 다중 클래스 분류는 softmax를 사용.
-
분류 문제에선 CE(Cross Entrophy) 손실함수도 쓴다.
CE는 모든 샘플에 대한-log(올바른 클래스에 대한 예측 확률)의 합계로 볼 수 있다.
추정치가 1에 가까워지면 손실이 0에 수렴하고, 0에 가까우면 손실이 증가한다. -
KL 발산은 두 확률 분포 p와 q 간의 차이를 측정하는 방법이다.
최적화
파라미터(W)를 조정하여 모델이 데이터에 잘 맞도록 하는 과정
-
일반적으로 모델의 손실 함수가 최적화 하려는 목표함수.
-
θ=θ−η∇J(θ)
새 파라미터는 이전 파라미터에서 (학습률*목표 함수의 그래디언트)를 빼주는 방식으로 업데이트 된다. -
경사하강법, SGD, 미니배치 경사하강법, 모멘텀 등을 사용한다.
과제
- Linear Classifier를 pytorch 없이 numpy, pandas 같은 라이브러리들만으로 구현하는 과제를 진행했다.
함수 정리
- pytorch grad 계산
import torch
# 아래처럼 requires_grad 옵션을 True로 하면 계산된 연산들에 대해 기울기를 계산할 수 있다.
x = torch.tensor(7.0, requires_grad = True)
y = torch.tensor(-3.0, requires_grad = True)
f = x * y
print(x.grad) # None
f.backward() # 특정 스칼라값에 대해 계산된 grad를 텐서들에대해 역전파 한다.
print(x.grad) # tensor(-3.)
print(y.grad) tensor(7.)- scatter(산점도) 시각화
seaborn 라이브러리의 scatterplot()를 이용하면 두 변수간 관계를 점으로 시각화해서 보여준다. plt.show()는 그래프를 화면에 표시하는 함수.
import seaborn as sns
import matplotlib.pyplot as plt
sns.scatterplot(data=dataset, x='city', y='age')
plt.show()- dropna() : Pandas의 결측치 제거 함수
dataset에서 city와 age열의 결측치('NaN') 행을 제거해서 새로운 data를 생성하는 코드
data = dataset.dropna(subset=['city', 'age'])피어세션
-
오늘은 아직 팀 진도가 많이 안나가서 스몰 토크 위주로 피어세션을 진행했다. 점점 어색함이 풀리고 있어서 분위기가 좋아지고 있다.
-
dataset 오류 발생 시
# on_bad_lines='skip' 추가
dataset = pd.read_csv('/content/drive/MyDrive/Colab Notebooks/data/2018_2019_2020.csv',sep = ",", header = 0, on_bad_lines='skip')
회고
- 나중에 logit, sigmoid, softmax 비교 한번 해보자.
