Today I Learned

오늘은 광복절이라 간단하게 헷갈렸던 부분 정리만 하고 쉰다!!

---

np.dot()

사용하면서 어떨 때는 내적 계산에 쓰이고, 어떨땐 행렬 곱셈에 쓰여서 헷갈려서 공식 문서를 찾아보면서 알아봤다.

• 우선 헷갈리는 개념인 내적, 아마다르 곱, 행렬곱셈을 다시 정리해보자.

내적

두 벡터끼리 계산해 스칼라가 나오는 연산.
두 벡터의 대응하는 원소들을 곱한 후 모두 더한다.

• 트랜스포머에서 Q와 K의 유사도를 계산하기 위해 Q와 K의 내적을 구한다. 이때 Q,K 모두 벡터이므로 유사도는 하나의 스칼라값으로 나온다.

• 따라서 어텐션 함수는 QK^T로 내적을 구해 유사도 스칼라 값을 낸 뒤, 이를 벡터 차원수의 제곱근으로 스케일링하고, 이 값을 softmax에 적용해 확률분포로 변환한 뒤 V값을 곱해 가중합을 구하는 함수다!

Hadamard Product(아마다르 곱)

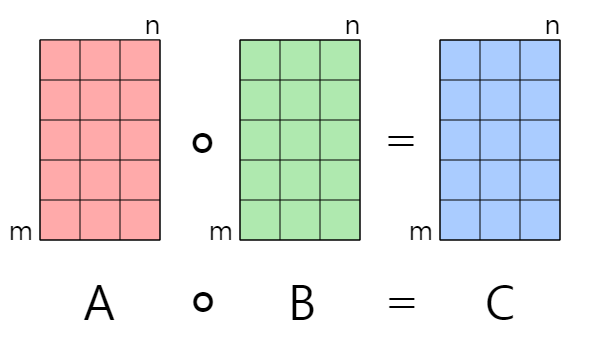
• 같은 크기의 행렬을 대응하는 원소끼리 곱해 새로운 행렬을 생성하는 연산

• 간단하게 * 연산자를 쓴다

import numpy as np

# 두 행렬 A와 B를 정의합니다.
A = np.array([[1, 2, 3],
              [4, 5, 6]])

B = np.array([[7, 8, 9],
              [10, 11, 12]])

# 요소별 곱셈 (아다마르 곱)
C = A * B

print(C)

행렬곱셈

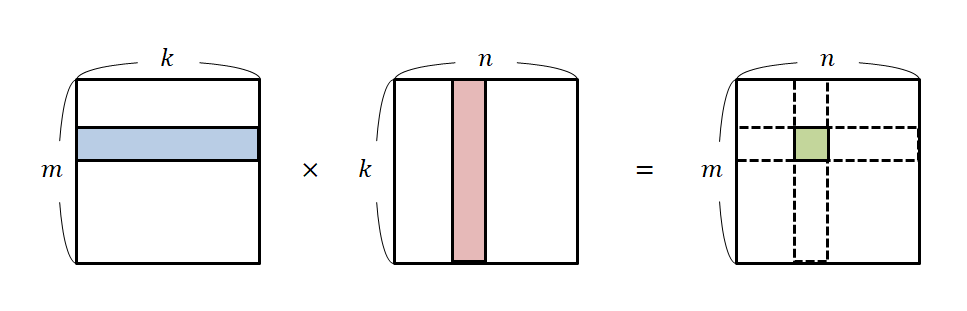
• 일반적으로 아는 행렬 곱셈. 앞행렬의 행과 뒤행렬의 열을 곱해준다.

---

In Numpy

• numpy 공식문서

numpy.dot(a, b, out=None)
Dot product of two arrays. Specifically,

If both a and b are 1-D arrays, it is inner product of vectors (without complex conjugation).

If both a and b are 2-D arrays, it is matrix multiplication, but using matmul or a @ b is preferred.

If either a or b is 0-D (scalar), it is equivalent to multiply and using numpy.multiply(a, b) or a * b is preferred.

If a is an N-D array and b is a 1-D array, it is a sum product over the last axis of a and b.

If a is an N-D array and b is an M-D array (where M>=2), it is a sum product over the last axis of a and the second-to-last axis of b:

dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])
It uses an optimized BLAS library when possible (see numpy.linalg).

• 1차원 벡터 x 1차원 벡터 = 벡터 내적계산

import numpy as np

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
result = np.dot(a, b)  # 결과는 1*4 + 2*5 + 3*6 = 32

• 2차원 행렬 x 2차원 행렬 = 행렬곱셈
  파이썬 연산자 @를 쓰는 것과 결과는 같다.

import numpy as np

A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
result = np.dot(A, B) # 결과는 [[19, 22], [43, 50]]
result2 = A @ B
print(result == result2) # 결과는 [[ True  True], [ True  True]]

• 하나라도 scalar 값이면 스칼라곱 연산.
  numpy.multiply(a, b)이나 a * b가 권장된다.

• 1차원 벡터 x n차원 배열
  it is a sum product over the last axis of a and b.
  a,b 마지막 축을 기준으로 두 배열의 곱의 합을 한다.

import numpy as np

a = np.array([[[1, 2, 3],
               [4, 5, 6]],
              
              [[7, 8, 9],
               [10, 11, 12]]])
              
b = np.array([1, 0, 1])

result = np.dot(a, b)

print(result)
"""
[[ 4 10]
 [16 22]]
"""

• n차원 배열 x m차원 배열
  it is a sum product over the last axis of a and the second-to-last axis of b
  a의 마지막 축과 b의 뒤에서 2번째 축을 기준으로 sum product를 한다.
  즉, a의 각 행과 b의 각 열끼리 순서대로 내적을 수행한 결과를 반환한다.
  이 경우에는 np.tensordot를 이용해서 축을 지정해 곱하는 걸 권장한다.
  np.tensordot(a, b, axes=([axis_a], [axis_b]))

import numpy as np

tensor_A = np.array([[[1, 2]], [[3, 4]]])
tensor_B = np.array([[[5], [6]], [[7], [8]]])
result_tensor = np.dot(tensor_A, tensor_B)
print(result_tensor)
"""
 [[[[17]
   [23]]]
 [[[39]
   [53]]]]
"""

참고 블로그 : jimmy-ai