Today I Learned
오늘 배운 내용은 변분 추론!
강의 복습
Jensen's Inequality
 이미지 출처 : probabilitycourse
이미지 출처 : probabilitycourse
-
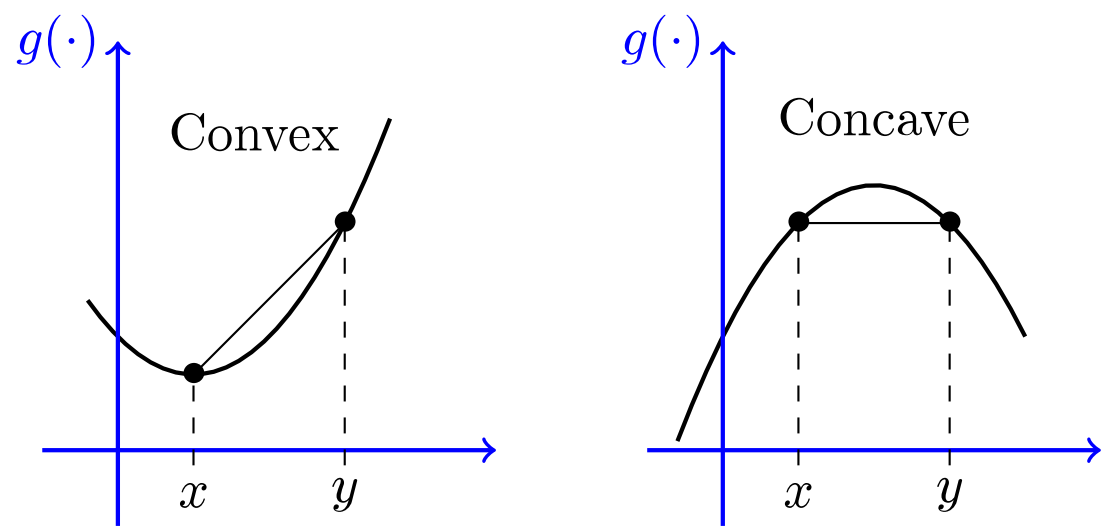
Convex function
아래로 볼록한 형태의 함수. 두번 미분 시 0 이상 ex) x, ,
기대값을 구한뒤 convex 함수에 넣은 것은 함수에 넣은 뒤 기대값을 구한 것보다 작거나 같다. -
Concave function
위로 볼록한 형태의 함수. 두번 미분 시 0 이하 ex) log x
기대값을 구한뒤 concave 함수에 넣은 것은 함수에 넣은 뒤 기대값을 구한 것보다 크거나 같다. -
함수가 밖에있는게(나중에 적용) 크면 concave, 안에 있어서 먼저 적용한게 크면 convex
-
서로 -를 붙이면 상대방으로 바뀐다. ex) -log x는 convex, 은 concave
변분추론(Variational Inference)
베이지안 모델에서는 관측 데이터로 부터 정확한 사후 확률 분포를 계산하는 것이 매우 어렵다(intractable). 따라서 직접 계산하기 보다는 근사화하는 방법을 사용한다. 변분추론은 원래의 복잡한 분포를 직접 계산하는 대신, 상대적으로 다루기 쉬운 분포를 선택해 원래 분포를 근사한다. 이 과정에서 두 분포간 차이를 최소화하는 것이 목표다.
-
복잡한 확률 모델의 잠재변수를 추정할 때 효율적이다.
-
잠재변수
관측된 데이터로부터 직접적으로 알 수 없는 숨겨진 변수
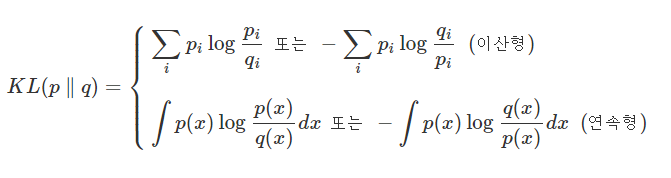
-
주어진 복잡한 분포 p를 다루기 쉬운 분포 q로 근사한다. 두 분포 사이의 차이를 측정할 때 사용하는 척도가
KL발산이다. 즉, KL발산을 최소화 하는 분포 q를 찾는 것이다.
KL발산은 p와 q의 분포 차이를 log ratio()를 통해서 측정한다. -
분포의 유사도 측정에는 f-divergence, H-divergence, IPM이 있는데, KL발산은 특정한 형태를 띈 f-divergence중 하나다.
-
KL발산은 위의 Jensen's Inequality를 적용하면 0 이상의 값을 가진다.
두 분포가 동일하면 0이다. 그리고 KL발산은 -log 함수이기 때문에 convex모양이다.
Mean-Field Variational Inference
변분추론에서 가장 널리 사용되는 방법
-
변분추론의 근사 분포를 선택할 때 독립성 가정을 적용한다.
여러 잠재변수가 서로 독립적이라고 가정해서 복장한 공동 분포를 단일 변수의 곱으로 표현할 수 있다. -
주어진 모델의 잠재변수 z=()에 대해 MFVI는 근사분포 q(z)를 아래와 같은 곱의 형태로 근사한다. 즉, 모든 잠재변수 는 서로 독립적인 분포로 근사된다.
- ELBO(Evidence Lower Bound, 증거 하한)
변분추론의 목표는 KL발산은 최소화하는 것 = 이는 수학적으로 ELBO를 최대화 하는 것이다.
-
위의 식에서 p(x,z)는 모델의 결합 확률 분포고, q(z)는 근사 분포다. ELBO를 최대화 함으로 써 근사 분포가 실제 분포에 가까워진다.
각 를 최적화해 ELBO를 최대화하면 근사 분포가 최적화 된다. -
독립성 가정때문에 계산이 단순화되어서 효율적이고 각 잠재 변수가 독립적이라 병렬처리에도 유리한 장점이 있다. 하지만 가정때문에 실제로 잠재변수 간 상관관계가 있으면 근사 정확도가 떨어지고 복잡한 분포를 정확하게 근사하기 어려운 경우가 있다.
과제
- AutoRec 모델 구현 중 관측된 데이터에 대해서만 loss를 계산하기 위해 criterion의 outputs에 * torch.sign(inputs)를 적용한다. 이 코드는 력이 0이 아닌 위치에 1을, 0인 위치에 0을 반환하므로, 관측된 데이터만 선택된다.
가중치가 무한정 커지는 것을 제한하기 위해 L2 정규화를 적용하는건 weight_decay_loss 함수를 사용한다.
def weight_decay_loss(model, lambda_value):
l2_reg = None
for param in model.parameters():
if l2_reg is None:
l2_reg = param.norm(2)
else:
l2_reg = l2_reg + param.norm(2)
return lambda_value * l2_reg
# 모델 학습
for epoch in range(num_epochs):
running_loss = 0.0
for data in train_loader:
inputs = data[0]
optimizer.zero_grad()
outputs = model(inputs)
# 여기 #
loss = criterion(outputs * torch.sign(inputs), inputs) + weight_decay_loss(model, lambda_value)
# 여기 #
loss.backward()
optimizer.step()
running_loss += loss.item()
running_loss = running_loss/len(train_loader)피어세션
-
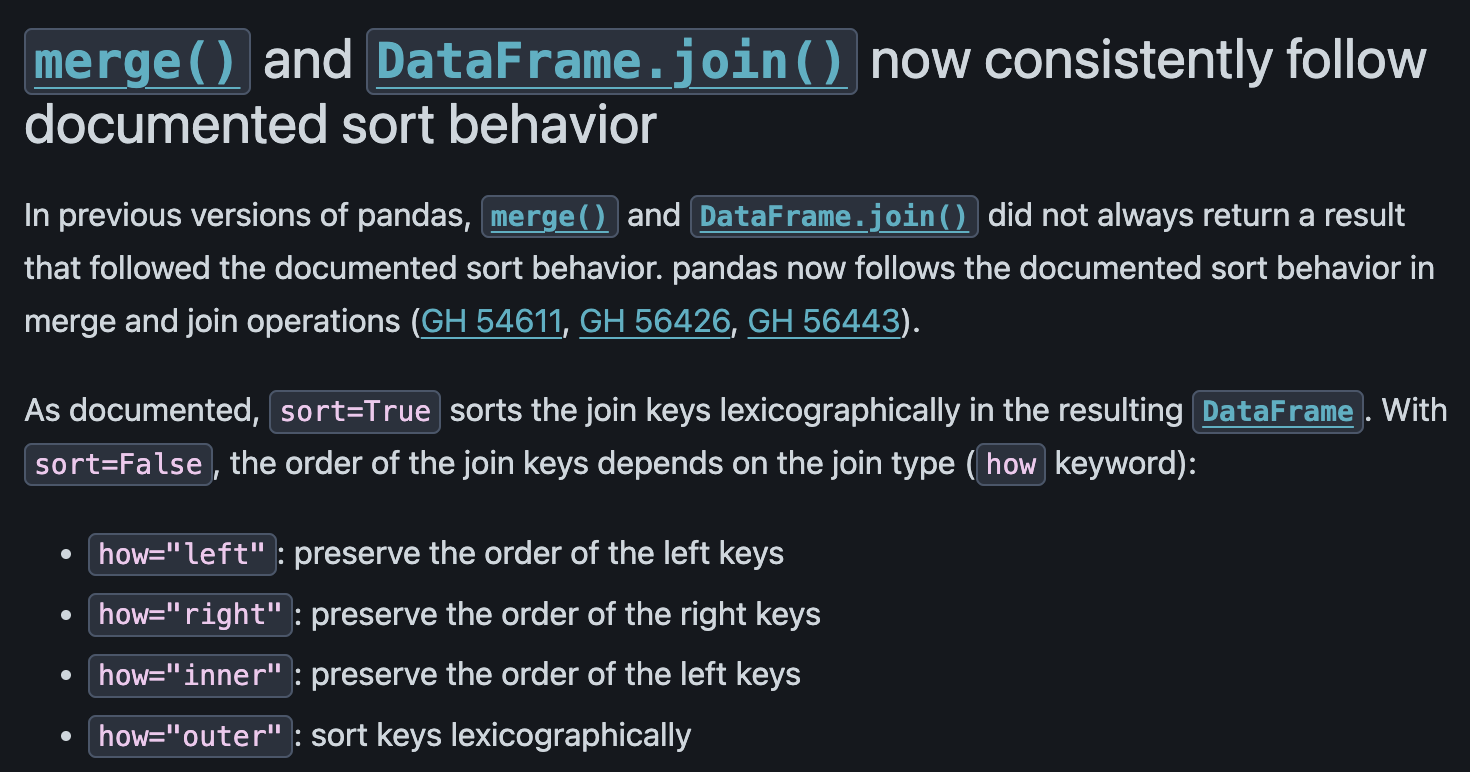
과제에서 pandas 버전에 따라 Merge 관련 sorting 로직이 달라져서 상위 5개를 input으로 집어넣는 과제에서 결과가 달라지는 것을 확인했다.
-
다음주가 끝나고 시작되는 프로젝트들에 대한 얘기를 했다. 한편으로는 막막하면서 주제가 재밌어 보여 기대가 됐다.
회고
- 오늘은 진도 쳐내는게 너무 힘들었다. 변분추론 내용도 어려웠을 뿐더러 과제도 만만치 않아 힘들었다. 내일도 진도 어느정도 나가서 다음주에 고통받지 않게 해야겠다.
