240828 TIL #478 AI Tech #17 Git - 2 / 생성모델 / VAE

김춘복·2024년 8월 28일

TIL aitech

TIL : Today I Learned

목록 보기

479/543

Today I Learned

오늘은 git 강의 마지막날! git강의와 생성모델에 대해 공부했다.

Git 특강

checkout은 HEAD를 바꾼다.
reset은 만약 attached 상태면 HEAD의 Branch를 바꾸고,
Dettached상태면 checkout과 같다.
merge를 했다가 취소하고 싶으면 merge 전 단계로 reset한다.
다시 복원하고 싶어도 git reset --hard 커밋hash 식으로 쓰면된다.
직전 작업을 취소하고 싶으면 git reset --hard HEAD@{1}
rebase
merge와 비슷하지만 merge는 다른 두 브랜치를 합치는 거라면(복잡한 진실)
rebase는 두 브랜치를 마치 한 브랜치였던것 처럼 2갈래 커밋들을 다 한갈래로 일원화 하는 것이다.(단순한 거짓말) 둘 다 결과는 같다.

Conflict

merge할 때 merge주체, merge상대, 공통 조상까지 3개의 commit을 3자대면시켜서 공통 조상에서 수정한 부분을 업데이트 시키는 식으로 바뀐다.
근데 주체와 상대 둘 다 공통조상에서 수정된 부분의 코드는 conflict가 발생한다.
현재 변경사항 수락(accept current change)
merge의 주체(HEAD가 가르키고 있던 브랜치)가 가진 변경만 수용한다.
수신 변경 사항 수락(accept incomming change)
merge하려는 상대 브랜치가 가진 변경만 수용한다.
두 변경사항 모두 수락
두 코드 모두 담음.
병합편집기에서 확인시 직접 수정 가능하다.
코드 수정 후 다시 커밋하면 merge 완료!

원격 저장소 github

일반적으로 원격저장소는 origin이라고 명명한다.
로컬과 원격을 연결하면 git graph상에 main/origin도 뜬다.
git remote remove origin을 하면 원격 연결이 해제된다.
git commit --amend -m "커밋 메세지" 를 하면 HEAD가 가르키는 커밋의 커밋 메시지를 수정할 수 있다. 단, 원격에 이미 올린건 수정하면 안된다.
pull = fetch + merge
fetch는 원격 저장소의 최신 변경 사항을 가져오지만, 로컬 브랜치는 변경하지 않는다.
pull이 fetch를 수행해 최신 변경 사항을 가져와서 merge까지 해서 로컬 브랜치를 변경하는 명령어다.
sync = pull + push
한 저장소로 여러명이 협업하는 경우 한쪽이 push로 올리면 다른 쪽은 pull을 해야 push를 할 수 있다. pull 과정에서 conflict가 발생하면 그걸 해결해야 push를 할 수 있다.

Pull Request & Issue

issues : 협업을 위한 게시판 역할. vscode 확장프로그램으로도 작성 가능.
커밋 메세지에 Fixes #2 처럼 n번째 이슈를 #으로 쓰고 Fixes로 명시해두면 자동으로 이슈가 닫히게 할 수 있다.

보통은 커밋 하나를 하더라도 branch를 파서 나가서 작업을 수행한 뒤에, Pull Request를 요청한 다음 허가를 받아서 main과 merge한다.
일반적으로 새 기능 만들때는 feature/login 이런식으로 feature를 브랜치 명 앞에 둔다.
PR을 날리고 승인이 나면 원격 저장소 상에서 main이 branch를 merge한다.
그 뒤에 main으로 checkout해서 pull을 땡기면 브랜치가 merge되어있다.

강의 복습

생성모델

주어진 훈련 데이터로 학습한 뒤, 이를 바탕으로 새로운 데이터를 만들어내는 데 사용하는 모델

데이터와 label이 같이 주어지거나(x,y) 데이터만 주어진다(x).
이때 x 데이터의 모집단 분포를 알고싶은데, 알 수 없으니 x에대한 모델을 만들어 추론한다.
따라서, 훈련 데이터는 Pdata(x) 실제 데이터가 따르는 확률 분포, 생성데이터는 Pmodel(x) 모델이 학습한 확률 분포.
생성모델을 통해 데이터의 hidden, underlying, 내재적인 패턴과 구조를 알 수 있다.
생성모델에는 VAE, GAN, Autoregressive Models 등이 있다.
GAN은 생성자와 판펼자 두개의 신경망을 이용해 학습한다. GAN의 결과물은 실제 데이터와 유사하지만 어떻게 생성됐는 지 해석하기 어려워 블랙박스 모델로도 여겨진다.
GAN에 대한 내용은 TIL #425 참고.

Graphical Model

변수들간의 관계를 그래프 구조로 표현하여 복잡한 확률 분포를 다루는 모델

노드는 확률변수. 엣지는 확률변수간의 의존성. 엣지가 없으면 조건부 독립, 있으면 조건부 의존성.
클래스 Y -> $X_j$ . 특정한 클래스(ex.강아지, 고양이)에서 이미지X를 생성함.

Plate Notation

그래피컬 모델에서 반복구조나 여러 변수를 효율적으로 표현하는 표기법

플레이트는 그 안의 노드(확률 변수들)과 엣지를 그룹화한다.
플레이트 한쪽에 숫자(n)는 이 그룹화된 구조가 n번 반복된다는 것.
예시. Gaussian Mixture Models(GMM)

p(x) = \sum_{k=1}^{K} \pi_k \mathcal{N}(x \mid \mu_k, \Sigma_k)

$\pi$ 는 분포별 비중. k는 가우시안 분포의 개수

$Z_n \sim Multinomial(\pi)$
$X_n \sim Gauusian(\mu_{Z_n}\sum_{Z_n})$ 이므로 아래의 그림으로 표현할 수 있다.

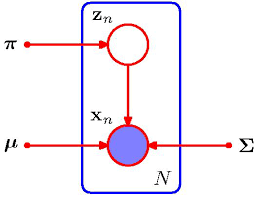이미지 출처 : stackexchange

VAE (Variational Autoencoder)

주어진 데이터의 잠재공간을 학습해 새로운 데이터를 생성하는 데 사용되는 모델

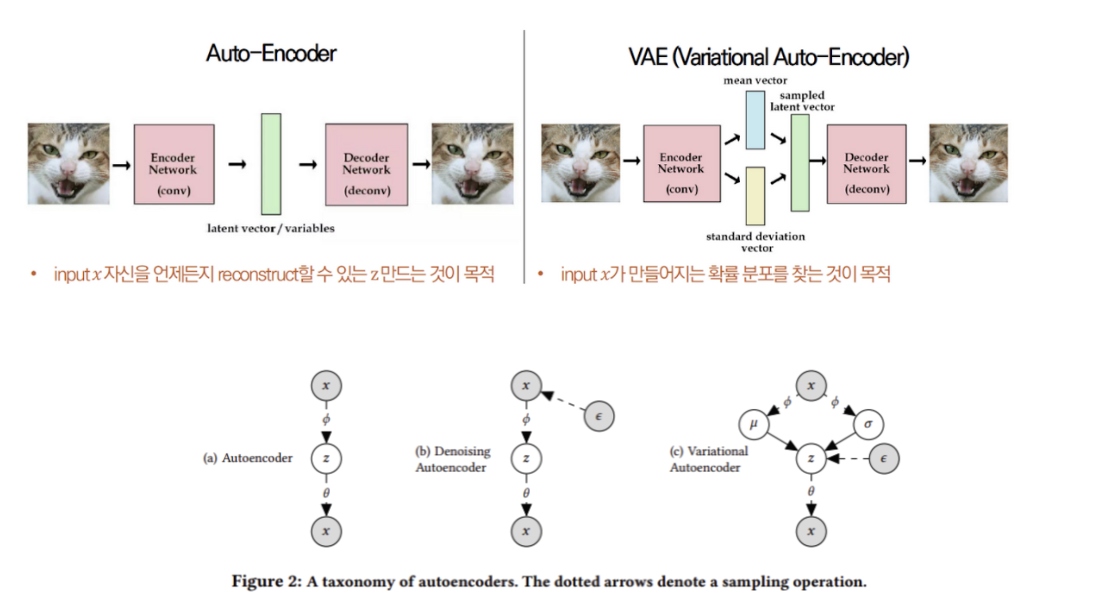이미지 출처 : huidea

Vanila AutoEncoder
Encoder에 input 데이터 x가 들어오면, 중간에 hidden layer z를 거쳐,
Decoder의 output layer에서 x'을 복원한다.
그래서 $||x - x'||^2$ (L2 노름의 제곱)즉, x와 x'의 차이를 줄이는 것이 목표
이를 위해 hidden layer에서 학습을 진행한다.
불필요한 데이터를 제거(압축)해서 차원축소를 하려는 목적으로 사용되기도 한다.
MNIST 숫자 손글씨 데이터로 예를 들면, 픽셀단위로 따지면 28x28=784개의 픽셀, 즉 $2^{784}$ 경우의 수를 따져야 하지만, 0~9까지 10개의 패턴으로 따지면 훨씬 경우의 수를 줄일 수 있다.
VAE는 위의 AutoEncoder의 변형형태로 데이터의 잠재 변수를 명시적으로 모델링하고 이를 통해 새로운 샘플을 생성한다.

KL발산

KL발산 : $D_{KL}(q(z|x)||p(z))$ 는
x(input)가 주어졌을 때 잠재변수 z의 확률분포(posterior)와
잠재변수 z의 사전(prior) 분포 p(z)가 얼마나 가까운지 먼지 나타낸다.
KL발산 값이 작으면 가깝다고 보므로 값을 낮추는게 목적이다.
잠재변수z의 확률 분포는 p(z)는 기본적으로 평균 0, 분산 1인 정규분포 $N(z;0,1)$ 를 따른다고 가정한다. 그리고 사후 확률 분포 q(z|x)는 $N(z;\mu(x), \sigma^2(x))$ , 즉 x의 평균과 분산을 따르는 정규분포로 가정한다.
KL(q||p) = $\int_x q(x)log\dfrac{q(x)}{p(x)}dx= \Bbb{E}_q[log(q) - log(p)]$
$log\dfrac{q(x)}{p(x)}$ 를 q에대해서 적분한 값을 로그의 차 equation으로 변환.
E는 expectation(기댓값)

Loss function

위의 식에 q와 p에 가우시안(정규) 분포 식을 대입하면 최종 목적식이 나온다.
앞부분은 Reconstruction loss, 뒤의 KL 발산은 Regularization loss라 한다.

Loss Function : L_i = - \Bbb{E}_{z\sim q_\phi(z|x_i)}[log p_\theta(x_i|z)] + KL(q_\phi(z|x_i)||p(z))

q밑에 $\phi$ 는 뉴럴 네트워크 층에서 학습해야하는 w,b같은 파라미터들을 의미한다.
$P_\theta$ 는 decoder의 뉴럴네트워크 파라미터.

실제로 모델링 적용할 때는 covariance를 identity로 가정하면 MSE Loss와 같아지기 때문에 MSE를 적용을 많이 한다. 혹시 x가 binary 흑백이미지면 Cross-Entropy 베르누이 분포를 적용한다.
앞식 E(기댓값)을 구하는건 특정 S개 만큼 샘플링해서 평균쳐서 계산한다.(몬테카를로예측)
뒷 식 KL 발산은 z를 샘플링할 필요가 없이 정확하게 값을 구할 수 있다.
$-\dfrac{1}{S} \sum_{s=1}^S[[log p_\theta(x_i|z_s)]]$

reparameterization trick

잠재변수 z를 샘플링하는 과정에서 직접 샘플링을 하면 신경망을 통해 미분이 불가능해진다.
미분이 필요한 이유는 VAE를 학습하는 과정에서 역전파를 수행해야하기 때문이다.
이 미분가능성을 해결하기 위해 reparameterization trick이 사용된다.
이를 통해 가우시안 분포의 파라미터(평균, 분산)을 조절하면서 잠재변수를 샘플링할 수 있고, 직접 샘플링하는 것보다 평균, 분산을 이용하기 때문에 더 효율적이고 안정적이다.
reparameterization trick: $z = \mu(x) + \sigma(x) \cdot\epsilon$
인코더 network에서 출력된 평균 벡터 더하기 표준편차 벡터 곱하기
N(0,1)에서 샘플링된 무작위 노이즈 $\epsilon$
이 식은 샘플링 과정을 분리해 표준정규분포에서 무작위 변수 $\epsilon$ 을 통해 z를 계산한다.
이 식은 정규분포의 선형변환 성질을 이ㅛㅇㅇ한 것으로 z가 $N(\mu,\sigma^2)$ 을 따르게 한다.
이러면 무작위성은 $\epsilon$ 에만 의존하기 때문에 $\mu$ 와 $\sigma$ 는 여전히 신경망의 출력이므로 미분이 가능해 전체 네트워크의 학습이 가능해진다.
activation 함수는 covariance가 양수가 나와야 하므로 softplus함수를 많이 사용한다.

회고

생활코딩님의 git강의를 매우 감명깊게 들었다. 강의 방식도 신선했고 그동안 알지 못했던 git의 원리를 제대로 알 수 있는 좋은 시간이었다.
본격적으로 RecSys 강의를 듣는데 수식파트가 매우 어렵다. 하나하나 검색해보면서 공부하는데 아직 힘들다. 좀 더 수학쪽으로 열심히 공부해서 이해해보자!