240903 TIL #483 AI Tech #22 Data Attribution 데이터 가치 측정 방법

김춘복·2024년 9월 3일

TIL aitech

TIL : Today I Learned

목록 보기

484/571

Today I Learned

오늘 배운 내용은 다양한 Data Attribution 방법들(Influence Function, Data Shapley, DVRL, Data-OOB)을 공부했다.

강의 복습

Data Attribution(데이터 가치평가)

데이터를 사용해 어떤 성과가 발생했는지 파악하고, 그 데이터의 기여도를 평가

Feature Attribution는 output에 각 feature가 얼마나 기여했는지 평가 ex)Grad CAM
반면 Data Attribution는 training data instance 마다 평가를 하는 방식.
Explainability
Data Attribution을 활용해 output을 도출하는데 가장 크게 기여한 data를 제시해 설명할 수 있다.
Model Diagnosis
noisy한 데이터로 학습 시키면 성능이 저조해진다. Data Attribution을 이용하면 test dataset에 대해 loss가 작아지도록 기여하는 정도를 각 training data set 마다 계산할 수 있어 어떤 dataset을 제거해야 훈련이 잘 될 지 알 수 있다.

Influence Function

모델의 예측 결과나 학습 과정에 특정 데이터 포인트가 얼마나 영향을 미치는지를 평가하는 방법

특정 데이터 포인트가 모델의 매개변수 추정에 얼마나 영향을 미치는지 측정한다.
즉, 특정 데이터를 추가 or 제거했을때 모델이 어떻게 변할 지 근사해서 분석한다.
IF를 활용해 특정 data point가 삭제되거나 추가될 때의 loss 변화량을 추정할 수 있다.
즉, 각 data point마다 중요도를 측정할 수 있다.
이는 추천시스템에서 중요한 Explainability! 추천에 대한 이유로 활용할 수 있다.
Unlearing : 이미 잘 학습된 RecSys에서 특정영역을 삭제하는 방법론으로도 쓰인다.
데이터 증강같은 방법을 통해 변형된 데이터도 이를 통해 측정할 수 있다.

기본 아이디어

Empirical Risk
모델이 훈련 데이터에 대해 수행하는 예측의 평균 손실 = $\dfrac{1}{N} \sum_{i=1}^n L(z_i, \theta)$
기본적인 손실함수는 empirical risk를 가장 최소화하는 파라미터를 찾는 것
$\hat\theta = \argmin_{\theta \isin\Theta} \dfrac{1}{N} \sum_{i=1}^n L(z_i, \theta)$
특정한 data z가 제거되었을 때 empirical risk와 그때의 파라미터는 아래와 같다.
$\hat\theta_{-z} = \argmin_{\theta \isin\Theta} \dfrac{1}{N} \sum_{z_i=z}^n L(z_i, \theta)$
결국 서로의 파라미터의 차이는 다음과 같다. $\hat\theta_{-z} - \hat\theta$
하지만 이 방법(LOO, Leave-one-out)은 시간이 오래걸리는 매우 비효율적인 방법.

Perturbation

원래의 상태에서 노이즈를 추가해 약간의 변화를 주는 것

아래의 식에서 $\epsilon = -1/n$ 이 되면 z를 쉽게 제거할 수 있다.
$\hat\theta_{e,z} = \argmin_{\theta \isin\Theta} \dfrac{1}{N} \sum_{i=1}^n L(z_i, \theta) + \epsilon L(z,\theta)$
파라미터 변화량 : $\Delta_\epsilon = \hat\theta_{e,z} - \hat\theta$
$\Delta$ 는 변화량, $\nabla$ 는 기울기를 나타낼때 사용하는 기호다.
Influence Function은 Perturbation의 결과로 모델이 받은 영향을 수학적으로 근사한다.
$H_{\hat\theta} = \dfrac{1}{N} \sum^n_{i=1} \nabla^2 L(z_i, \hat\theta)$ H는 평균 손실함수의 곡률을 나타내는 Hessian 행렬이다. 이 행렬이 클수록 모델이 현재 위치에서 더 안정적이다. 여기선 $H^{-1}$ 이 있다는 가정하에 진행한다. Hessian 행렬때문에 많은 연산이 필요해진다.
최종적으로 데이터 포인트 $z_i$가 매개변수 $\hat\theta$에 미치는 영향 $I(z_i)$는 아래와 같이 정의 된다.
$I(z_i) = -H^{-1}_\theta\nabla L(z_i, \hat\theta)$
기울기 $\nabla L(z_i, \hat\theta)$ 는 특정 데이터포인트가 손실함수에 미치는 직접적인 영향이다.
결과적으로 $I(z_i)$ 가 크면 해당 데이터 포인트가 모델의 매개변수에 강하게 영향을 끼친다.

Data Shapley

Shapley Value라는 게임 이론 개념을 데이터 분석에 적용해 데이터 포인트의 중요성을 평가하는 방법

Shapley Value : 게임 이론에서 플레이어가 게임의 결과에 미친 기여도를 공정하게 계산하는 방법
mislabeled dataset이나 noisy dataset을 탐지할 수 있다.
모든 가능한 데이터 조합에 대해 특정 데이터가 있을 때와 없을 때의 모델 성능 차이를 평균내어 가치를 평가한다.

방법

Equitable valuation 조건을 만족하는 유일한 식

\phi_i = C \sum_{S \subseteq D-\{i\}} \dfrac{V(S \cup \{i\}) - V(S)}{\frac{n-1}{|S|}}

C는 임의의 상수, $\phi_i$ 는 i번째 데이터의 가치, $S \subseteq D-\{i\}$ 는 i 데이터를 뺀 D데이터 조합의 부분집합인 S. S에 데이터 i를 추가했을 때 $V(S \cup \{i\})$ 랑 추가하지 않았을 때V(S)랑 가치를 비교한다.
하지만 이 계산을 하려면 엄청난 연산이 필요하다. 그래서 아래의 식으로 근사한다.
C=1/n!로 설정하고 $\Pi$ 를 n!에 대한 Uniform 분포로 설정한다.
$\phi_i = \Bbb{E}_{\pi \sim \Pi}[V(S^i_\pi \cup \{i\}) - V(S^i_\pi)]$
$S^i_\pi$ 는 dataset n개를 random permutation(무작위 순열)한 뒤 data i의 위치 직전까지 data들의 집합(i 미포함)이다. 예를들어 i가 처음에 위치하면 이는 공집합이다.
즉, 이 식은 데이터 포인트 i를 추가했을 때 가치가 얼마나 증가하는지를 전체 가능한 순열에 대해 평균하여 i의 기여도를 평가하는 식이다.
n!개 줄세워서 i번째 데이터 전까지 가치측정하고 거기서 i 데이터 포함해서 가치 측정해 그 차이를 계산하고..
이렇게 n!개를 다 하면 너무 연산이 많아지니 monte carlo 근사로 몇개를 샘플링해서 진행한다.

DVRL

Data Valuation using Reinforcement Learning
강화학습 기반의 Data Attribution

위의 IF랑 Data Shapley는 이미 학습이 끝난 뒤 validation이나 test에서 도움이 되는 훈련 data를 찾기 위해 진행하는 것이고, DVRL은 학습 시작부터 validation data에 대한 성능을 올리기위한 training dataset valuation이다.
기존과 다르게 데이터가 대규모인 대형 모델에도 적용이 되는 scalable한 알고리즘이다.

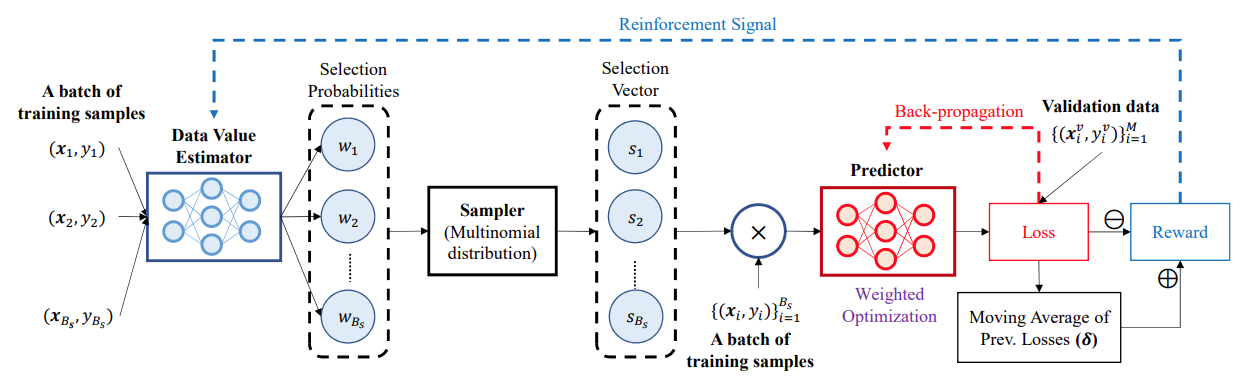이미지 출처 : Data Valuation using Reinforcement Learning 논문

validation dataset 성능을 reward로 놓고, 해당 reward를 maximize로 하는 action으로 정한 뒤 강화학습을 진행한다. train dataset으로 학습 시키되 성능 평가는 validation dataset으로 한다.
단, test와 validation dataset이 동일한 분포에서 추출됐다고 가정한다.(이 때문에 현실에서 적용하기 힘든 경우가 있다.)
적은 sample data만으로 전체 training data를 학습하는 효과와 비슷한 성능을 낼 수 있다.
오히려 일부 데이터만 썼을 때 더 성능이 좋을 때가 있다.
validation data가 없으면 쓸 수 없어 현실적으로 적용하기 어려울 때가 있다.

Data-OOB

Bagging 기반의 데이터 샘플의 기여도를 평가 방법

단순하면서 강력한 성능을 보여준다. validation dataset이 필요 없으면서 scalable하다.
bagging은 여러 모델을 앙상블하는 방법론으로, 중복을 허용해 dataset을 샘플링하고 이 샘플들을 이용해 독립적으로 여러 모델을 훈련한 뒤 나오는 output을 앙상블하는 기법
대표적으로 random forest 방법이 있다.
OOB는 bagging의 샘플링 과정에서 제외한 dataset을 말한다. 즉 각 트리에서 훈련되지 않은 샘플이다. OOB에 특정 데이터가 있는 경우랑 없는 경우를 비교해서 가치를 측정한다. 그래서 특정 데이터가 OOB일 때, loss가 크면 중요하다고 여겨진다.
즉, 특정 데이터 포인트(OOB)가 모델 학습에 포함되지 않았을 때의 성능 감소를 측정하여 해당 데이터 포인트의 가치를 평가한다.
여러 번의 데이터 샘플링과 그에 따른 모델 재학습이 필요하긴 하지만, OOB에 여러 데이터가 들어갈 수 있으므로 한 트리에 여러 경우를 비교할 수 있어 LOO와는 다르게 scalable한 방법이다.