Today I Learned

오늘은 마르코프 연쇄 몬테카를로 방법(MCMC)에 대해 배웠다.

---

강의 복습

샘플링 방법

Inverse Transform Sampling

CDF F(x)의 역함수$F^{-1}(U)$를 사용해 임의의 샘플을 생성하는 방법.
하지만 특정한 분포에서만 가능해서 아래의 방법들을 사용한다.(정규화 상수를 알아야 한다?)

rejection sampling

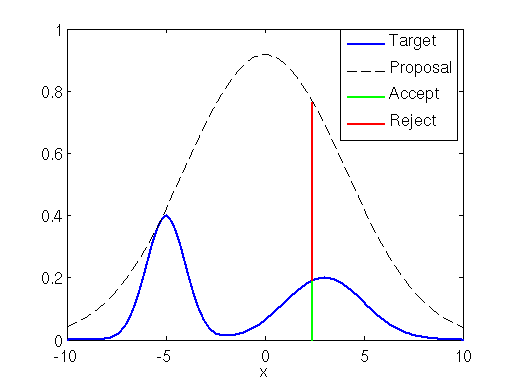이미지 출처 : happip-jh

목표분포 p(x)를 모두 포괄하면서 샘플링하기 쉬운 제안 분포 q(X)를 선택해서 둘 사이의 비율을 결정할 수 있는 상수 k를 결정한다. k는 아래의 식을 만족해야 한다.

• q(x)에서 샘플 z를 생성하고, 균등분포 U(0,1)을 따르는 샘플 u를 생성해서 생성된 u가 아래의 수락 확률 보다 작거나 같으면 z를 수락한다. 즉 위 그림의 target 안이면 accept한다.
  샘플링을 하기 위해선 확률의 역수배 만큼 더 해야한다(ex. 20%면 5번 해야 1개 accept)

Importance Sampling

목표 분포 p(x)에서 직접 샘플링하기 어려울 때, 다른 분포(중요도 분포)에서 샘플을 생성하고 생성된 샘플에 가중치를 부여해 원하는 분포를 근사하는 방법.

• 목표 분포 p(x)에서 샘플링하기 힘들 때, p(x)를 합리적으로 포괄하는 제안 분포 q(x)에서 샘플 z를 생성하고 각 샘플 z에 대해 가중치 $\tilde w(x) = \dfrac{\tilde p(x)}{\tilde q(x)}$를 계산해서 아래의 식처럼 가중평균을 구해 f(x)의 기대값을 추정해 사용한다. N은 샘플 수.

• 모든 샘플은 채택하되, 각 샘플의 중요도를 weight을 계산해 가중평균으로 더한다.
  즉, 샘플의 채택, 거부과정이 없다.

---

몬테카를로(MC) 근사

무작위 표본을 생성해 이를 기반으로 원하는 값(기대값, 확률 등)을 근사적으로 계산하는 방식

• random sampling 후 이 표본을 평균내서 원하는 양을 추정한다.
  복잡한 함수나 고차원 적분 문제에 적용한다.

• 표본 생성 - 함수 평가 - 평균 계산의 단계를 거친다.

• 어떤 f(x)든 간에 그 f(x)의 기대값은 표본의 평균과 유사($\approx$)하다.
  단 표본 $x_i$는 샘플 사이즈 N이 커야되고, 독립적으로 추출되어야 한다.

• $\hat f$의 분산은 N이 적으면 크고 N이 많아지면 작아진다.
  표본의 무작위성 때문에 noise가 발생하며, 중요한건 샘플링의 크기 N이다.

---

MCMC

마르코프 체인을 이용해 몬테카를로 샘플링을 수행하는 방법.

• 위의 샘플링 방법(rejection, importance)들은 z의 차원이 커지면 값을 구하기 힘들다.
  MCMC는 위의 방법들 보다는 상대적으로 계산하기 편하다.

• Markov Chain
  현재 상태가 바로 직전 상태에만 의존하고 과거나 미래 정보는 고려하지 않는 특성의 모델
  즉, 현재 생태를 기반으로 미래를 예측할 때 과거는 무시한다.

• Monte carlo 방법 : 무작위 샘플링을 통해 근사적으로 해결하는 방법

• Invariant(stationary) Distribution
  = target 분포. MCMC에서 연쇄가 반복된 후에 수렴하고 더이상 바뀌지 않는 안정된 분포.
  discrete MC(state space가 정수, 유리수)에서는 최소 1개 이상의 불변 분포가 존재한다.
  실수는 보장 x
  그리고 Irreducible(어느 state든 넘어갈 수 있을 때)하면서 Aperiodic(주기가 일정하지 않을 때)한 상태에선 유일한 stationary 분포를 가진다.

• MCMC는 현재 상태에 따라서 계속해서 제안(proposal)을 업데이트 해나가면서 추정한다.
  현재 상태를 기반으로 제안된 상태를 수용할지 결정하고, 이를 반복적으로 수행하면서 샘플을 생성해 전체 분포를 추정한다.

• 초기상태 $z_0$를 임의로 선택해서 현재 상태에서 다음 상태로 가는 규칙(전이 확률)을 정의한다. 그 뒤 규칙이 제안하는 상태를 수용할 지 거절할 지 결정한다. 이 과정을 반복해서 원하는 분포에 수렴하면 그 분포로 부터 샘플을 추출한다. 이전의 샘플은 버린다(burn-in)

• Metropolis-Hastings 알고리즘
  현재 상태에서 새로운 상태를 제안하고 이 상태를 수용할 지 확률적으로 결정하는 알고리즘 식
  새로운 상태 z'를 현재 상태 z로부터 제안분포 $q(z'|z)$에 따라 샘플링한 뒤 수용확률 $\alpha$에 따라 z'를 수용한다. 수용 확률은 아래와 같다. p(z)는 목표 분포다.

HMC

MCMC의 한 종류로 연속적인 고차원 확률 분포로부터 샘플을 생성하는 데 사용된다.

• 해밀토니안 역학(Hamiltonian Mechanics)
  시스템의 총 에너지를 모멘텀(p)와 위치(q)를 이용해 표현한다.

• 해밀토니안 함수 H(x,p)
  포텐셜에너지 U(x) + 운동에너지 K(p). M은 질량 행렬

• 가우시안 분포로 부터 모멘텀 p를 샘플링하고, 상태 x와 모멘텀 p를 업데이트 한다.
  해밀토니안 에너지의 변화를 비교하여, 샘플을 수용할지 여부를 결정한다. 샘플이 목표 분포에 맞게 수용되거나 거부된다. 수용된 샘플을 저장하고, 충분한 수의 샘플이 수집될 때까지 이 과정을 반복한다.

• 핵심은 위치에너지와 운동에너지를 이용해서 target 분포로 수렴시키기 위해 proposal을 계속 변화시키는 모델링. 즉, HMC는 모멘텀이 도입된 MCMC.

• 그래디언트 정보를 이용해 효율적으로 고차원 공간을 탐색하며, 일반적으로 다른 MCMC에 비해 빠르게 수렴한다.

---

피어세션

• Collaborative Filtering for Implicit Feedback Datasets 논문을 읽고 같이 논문에 대해 토론했다. 비용함수를 미분해서 $x_u$를 찾는 계산에서 이해를 못한 부분이 많았는데, 같이 보면서 풀어보니 이해가 됐다.

• (m x p) 크기의 A와 (p x n)크기의 B 행렬을 곱셈할 때 시간복잡도는 $O(m*p*n)$
  따라서, (n x f) 크기의 Y 행렬을 가정할 때, $Y^TY$의 시간복잡도는 $O(f^2n)$

---

멘토링

• 논문 효율적으로 읽는 법
  title -> abstract -> conclusion -> methodology + experiments 이까지 가볍게 있고
  상세하게는 다 보면된다.

---

회고

• MCMC는 얼추 이해는 했지만 강의 내용에 대해서는 아직 이해 못한 부분이 많다. 시간 여유가 있을 때 다른 자료를 찾아서 공부해보아야 겠다.