241007 TIL #508 AI Tech #43 Regression(선형회귀) 기법 총 정리

김춘복·2024년 10월 7일

TIL aitech

TIL : Today I Learned

목록 보기

510/571

Today I Learned

오늘은 쉬는날이지만 강의 진도를 나갔다. 오늘 공부한 내용은 회귀 기법!

Regression(회귀) 기법

선형회귀

독립변수 X와 종속변수 Y의 선형관계를 모델링

독립변수는 다른 변수에 영향을 받지않고 종속변수에만 영향을 끼친다고 가정한다.
하지만 실제 데이터에선 독립변수간의 상관관계가 있으며, 이때문에 다중 선형회귀에선 다중 공선성과 같은 문제를 다뤄야한다.
단순 선형회귀는 하나의 독립변수로 하나의 종속변수를 예측한다.
다중 선형회귀는 여러 독립변수로 하나의 종속변수를 예측한다.

선형회귀의 가정

선형성
X와 Y의 관계는 선형적(직선 형태의 관계)이어야 한다.
1,2,3은 잔차 플롯으로 검증할 수 있다.
독립성
잔차간의 상관관계가 없어야 한다.
특히 잔차가 무작위로 분포되어있어야 한다. 더빈-왓슨 테스트 같은 방법을 사용한다.
등분산성
잔차 분산은 독립변수의 값에 상관없이 일정해야한다.
즉, 독립변수에따라 잔차의 분산이 변하면 안된다.
이게 깨지면 이분산성이 나타나서 회귀 분석의 신뢰성이 떨어진다.
정규성
잔차는 정규분포를 따라야한다. Q-Q플롯으로 검증할 수 있다.
다중공선성 없음
독립변수들 간의 강한 상관관계가 없어야 한다.
분산 팽창 계수(VIF)가 10 이상이면 다중공선성이 있다고 판단한다.

최소제곱법(OLS)

Ordinary Least Squares. 예측값과 실제값의 차이(잔차, residuals)를 제곱합 한 값이 최소가 되도록 하는 직선을 찾는 방법.

잔차제곱합을 최소화하는 기울기와 절편을 찾는 방법.

정규화(Regularization)

회귀모델에서 과적합을 방지하고 더 일반화된 모델을 만들기위해 사용하는 기법

모델의 복잡성을 줄여 학습데이터에 너무 맞추게 하지 않고 일반화 성능을 높인다.
다중공선성을 해결한다.

Lasso(L1 정규화)

선형 회귀 모델의 회귀 계수 절대값 합을 최소화하는 정규화 기법

RSS + \lambda\sum^{p}_{j=1} |B_j|

RSS는 잔차제곱합. $\lambda$ 는 정규화 강도를 조절하는 하이퍼 파라미터
특정 회귀계수를 0으로 만들어 자동으로 feature selection을 수행하게 한다.
불필요한 변수를 제거해 모델을 간결하게 만들고, 과적합을 방지한다.
변수간 비선형 관계는 잘 처리하지 못하고, 상관관계 높은 변수가 제거될 수 있다.
다중공선성이 있으면 신뢰도가 떨어진다.

Ridge(L2 정규화)

회귀계수의 제곱합을 최소화하는 기법

RSS + \lambda\sum^{p}_{j=1} B_j^2

회귀계수가 너무 커지는 것을 막는다.
lasso와 달리 모든 회귀 계수에대해 제곱 페널티를 부여해서 계수의 크기는 줄이지만 0으로 만들지는 않는다.
과적합을 방지하며, 다중공선성 문제를 해결해준다. 하지만 불필요한 변수도 0으로 만들지는 않는다.

ElasticNet

Lasso와 Ridge의 장점을 결합한 방법

RSS + \lambda_1\sum^{p}_{j=1} |B_j| + \lambda_2\sum^{p}_{j=1} B_j^2

L1정규화와 L2정규화를 함께 적용해서 각자의 단점을 보완했다.
Ridge의 안정성과 Lasso의 특성 선택 모두를 활용할 수 있다.
하이퍼파라미터 \lambda의 조정이 더 중요해졌다.

딥러닝 Regression

딥러닝을 Regression에 활용하면 다층신경망을 통해 복잡하고 비선형적인 관계를 학습할 수 있어 전통적인 회귀 모델보다 성능이 높을 수 있다.

다만 예측 결과를 해석하는 데 어려움이 있을 수 있다.
딥러닝 학습과정에서 중요한 것은 loss가 계속 하락하는 추세인 지 확인하는 것
용어
다층신경망(MLP) : 입력층, 은닉층, 출력층으로 구성된 신경망. 복잡한 패턴을 학습하기위해 다층구조.
활성함수(Activation Funcion) : 신경망이 복잡한 비선형 패턴을 학습하도록 돕는 함수(ReLU, Sigmoid)
손실함수(Loss Function) : 모델의 예측값과 실제값 사이를 측정하는 함수. 모델은 학습을통해 손실함수의 오차를 최소화하려는 목표를 가진다.
최적화 알고리즘(Optimizer) : 손실함수를 최소화하기 위해 가중치와 편향을 업데이트하는 방법. (SGD, Adam, 경사하강법)
작동 원리
1. 입력 데이터 전달
2. 가중치 및 편향 적용
3. 활성함수 통과 : 비선형 변환
4. 은닉층 처리 : 은닉층 통과하면서 반복적으로 처리
5. 출력층 계산 : 마지막 출력층에서 최종 결과값 도출
6. 손실 계산 : 예측값과 실제값의 차이를 손실함수로 계산
7. 역전파 : Loss를 이용해 가중치와 편향 조정을 위해 역방향으로 경사 하강법을 적용
8. 가중치 업데이트: Optimizer에 따라 가중치가 업데이트

코드 예시

import torch
import torch.nn as nn
import torch.optim as optim

# 1. 다층신경망 모델 정의
class SimpleMLP(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(SimpleMLP, self).__init__()
        # 은닉층 정의
        self.hidden_layer = nn.Linear(input_size, hidden_size)  # 입력 -> 은닉
        # 활성함수로 ReLU 사용
        self.relu = nn.ReLU()
        # 출력층 정의
        self.output_layer = nn.Linear(hidden_size, output_size)  # 은닉 -> 출력

    def forward(self, x):
        # 은닉층에서 선형 변환 + ReLU 활성함수 적용
        hidden_output = self.relu(self.hidden_layer(x))
        # 출력층에서 선형 변환
        output = self.output_layer(hidden_output)
        return output

# 2. 입력 크기, 은닉층 크기, 출력 크기 설정
input_size = 10  # 예: 특성 10개
hidden_size = 5   # 은닉층에 5개의 뉴런
output_size = 1   # 예: 회귀 문제이므로 출력은 1개

# 3. 모델, 손실함수, 최적화 함수 설정
model = SimpleMLP(input_size, hidden_size, output_size)

# 손실 함수로 MSE 사용 (예: 회귀 문제)
criterion = nn.MSELoss()

# 최적화 함수로 Adam Optimizer 사용
optimizer = optim.Adam(model.parameters(), lr=0.001)

# 4. 더미 입력 데이터와 타겟 데이터 설정 (예: 배치 크기 10)
inputs = torch.randn(10, input_size)  # 10개의 샘플, 각 샘플은 input_size 크기
targets = torch.randn(10, output_size)  # 10개의 타겟 값 (회귀 문제라서 출력 1개)

# 5. 학습 과정 (순전파 -> 손실 계산 -> 역전파 -> 가중치 업데이트)
num_epochs = 100  # 100번 학습 반복

for epoch in range(num_epochs):
    # 순전파 (Forward Pass)
    outputs = model(inputs)  # 모델을 통해 예측값 생성
    loss = criterion(outputs, targets)  # 예측값과 실제 타겟 비교하여 손실 계산

    # 역전파 (Backward Pass)
    optimizer.zero_grad()  # 이전의 기울기(gradients) 초기화
    loss.backward()  # 손실값을 기준으로 역전파 진행

    # 가중치 업데이트
    optimizer.step()  # 최적화 함수가 가중치 업데이트 진행

    # 10번마다 손실 출력
    if (epoch+1) % 10 == 0:
        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')

Activation Functions

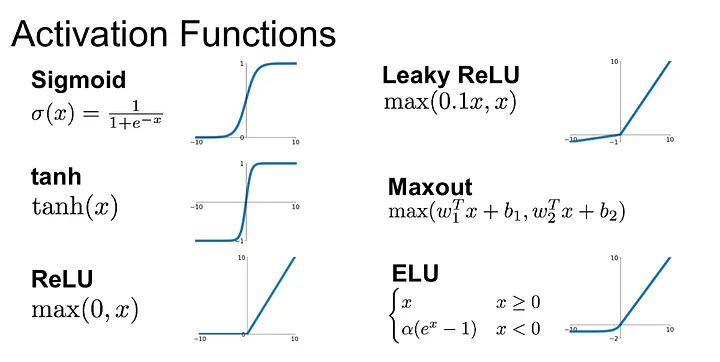이미지 출처 : medium.com/@shrutijadon

ReLU
간단한 계산, Gradient Vanishing 문제 해결, 딥러닝에서 가장 많이 사용
음수 값을 모두 0으로 변환해 특정 뉴런 학습 멈춤(Dead Neurons), Exploding Gradient 문제
Sigmoid
출력이 0~1범위에 연속적이라 확률값으로 해석이 가능해 이진분류문제에서 자주 사용
Gradient Vanishing 문제가 있고 출력 범위가 0~1이라 오히려 제한적이라고 볼 수도 있다.
Tanh
출력이 -1~1범위라 sigmoid보다 더 강력한 비선형성.
Gradient Vanishing 문제가 있고 지수함수라 계산이 다소 복잡하다.

Gradient Vanishing?
네트워크 층이 깊어질수록 역전파 과정에서 계산된 기울기(gradient)가 점점 작아져서 최적화 과정에서 가중치가 거의 업데이트되지 못하는 현상. 모델이 효과적으로 학습되지 않는다.
sigmoid, tanh 에서 더 심해진다.

Loss Function

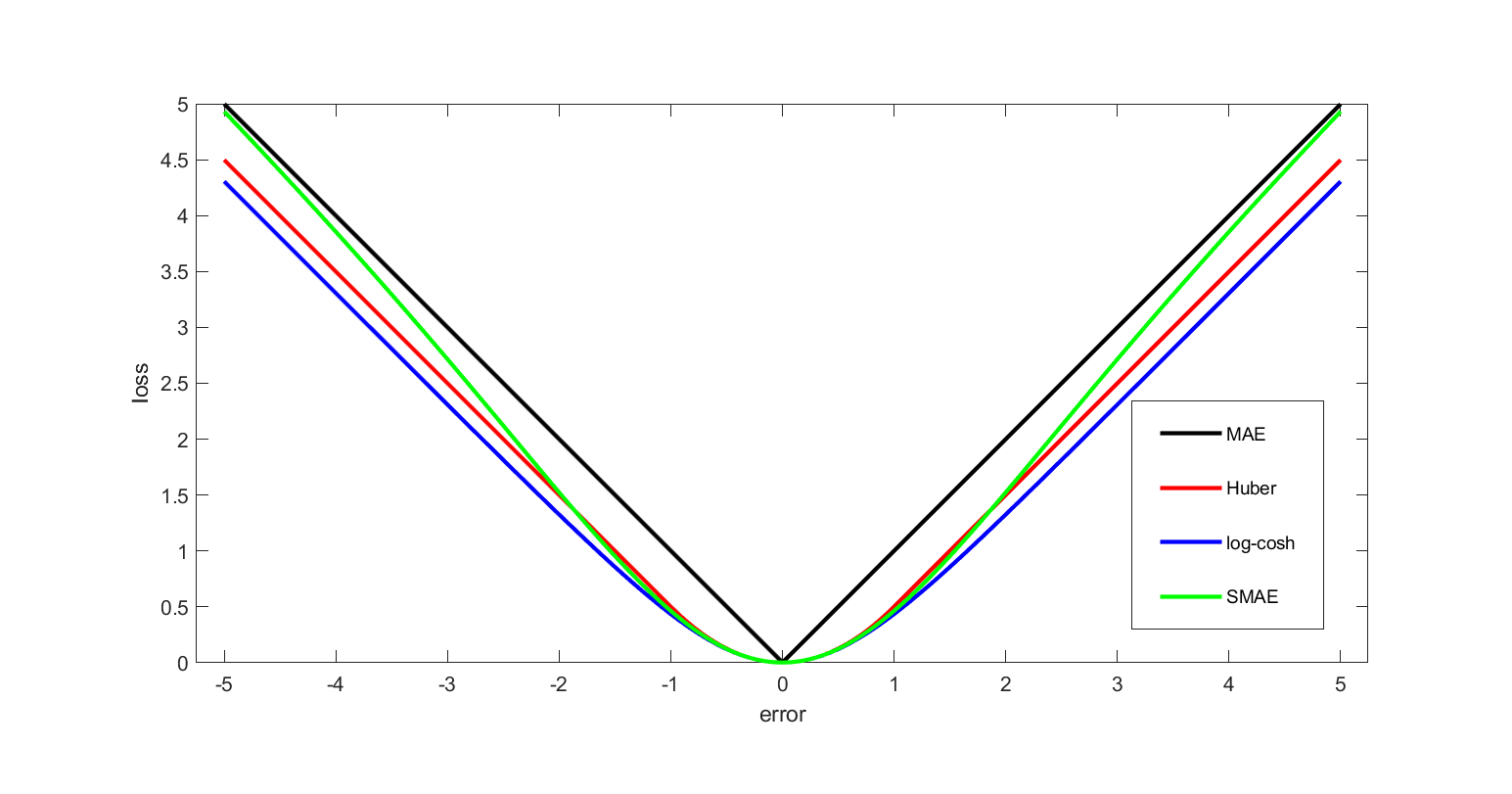이미지 출처 : wikimedia

손실 함수	용도	설명
Mean Squared Error (MSE)	회귀 문제	예측값과 실제값의 차이를 제곱하여 평균을 구함.
Mean Absolute Error (MAE)	회귀 문제	예측값과 실제값의 차이를 절대값으로 변환하여 평균을 구함.
Huber Loss	회귀 문제	오차가 특정값 미만일 때는 MSE, 이상일 때는 MAE로 계산하여 이상치에 민감하지 않음.
Binary Cross-Entropy	이진 분류 문제	예측 확률과 실제 레이블을 비교하여 손실을 계산.
Categorical Cross-Entropy	다중 클래스 분류 문제	각 클래스에 대한 확률과 실제 레이블을 비교하여 손실을 계산.
Hinge Loss	서포트 벡터 머신(SVM)	결정 경계와의 거리를 기반으로 손실을 계산.
Kullback-Leibler Divergence	확률 분포 간의 차이 측정	두 확률 분포 간의 차이를 측정하여 설명 능력을 평가.

과적합 방지기법

정규화(Lasso, Ridge, ElasticNet)
Dropout
학습과정에서 무작위로 뉴런을 비활성화시키는 방법
각 학습마다 비활성화되는 뉴런 조합이 달라져서 모델이 Robust 해진다.

김춘복

Backend Dev / Data Engineer

이전 포스트

241005 TIL #507 카카오 모빌리티 코테 후기

다음 포스트

241007 TIL #508 AI Tech #43 Regression(선형회귀) 기법 총 정리

TIL : Today I Learned

Today I Learned

Regression(회귀) 기법

선형회귀

선형회귀의 가정

최소제곱법(OLS)

정규화(Regularization)

Lasso(L1 정규화)

Ridge(L2 정규화)

ElasticNet

딥러닝 Regression

코드 예시

Activation Functions

Loss Function

과적합 방지기법

241005 TIL #507 카카오 모빌리티 코테 후기

241008 TIL #509 AI Tech #44 클러스터링(K-means / DBSCAN / GMM)

0개의 댓글