A Survey of Transformers (2021) 논문 스터디 - (1)

LLMs 관련 청강을 하게 됐는데, 교수님께서 꼭 읽어보라고 권해주신 survey paper다. 이 논문은 Transformer와 그 변형 (X-formers)들에 대해서 소개한다.

이 논문에 대해서는 이미 고려대학교 DSBA Lab에서 진행한 스터디가 있지만, 내 나름대로도 논문을 읽고 스터디를 해보려고 한다.

[원문] A Survey of Transformers (2021, arXiv)
[참고] Transformer survey study

논문 내용이 길어서 챕터별로 끊어서 스터디를 진행하려고 한다. 여기서는 Backgrounds의 Vanilla Transformer model에 대해서 다룬다.

---

Vanilla Transformer

vanilla Transfomer 모델은 sequence-to-sequence 모델로, encoder와 decoder 한 쌍으로 구성된다. 각 encoder, decoder는 $L$개의 동일한 블록을 쌓아올린 형태이다. 각 encoder 블록은 주로 multi-head self-attention 모듈과 position-wise feed-foward network(FFN)으로 구성되어 있다.

• position-wise feed-foward network(FFN) 입력 시퀀스의 각 position마다 별도로 적용되는 FFN으로, 각 위치의 표현 벡터를 별도로 처리하여 더 높은 차원의 표현으로 매핑하는 역할을 한다.
  

더 깊은 모델을 설계하려면, 각 모듈 주변에 residual connection(잔차 연결)을 사용하고, 그 뒤에 Layer Normalization 모듈을 사용한다. encoder 블록들과 비교하면, decoder 블록들은 multi-head self-attention 모듈과 position-wise FFNs 사이에 cross-attention 모듈을 추가로 삽입한다. 더불어, decoder의 self-attention 모듈은 각 position이 이후의 position에 주목하지 못하도록 조정된다. vanilla Transformer의 전반적인 구조는 아래 Fig. 1과 같다.

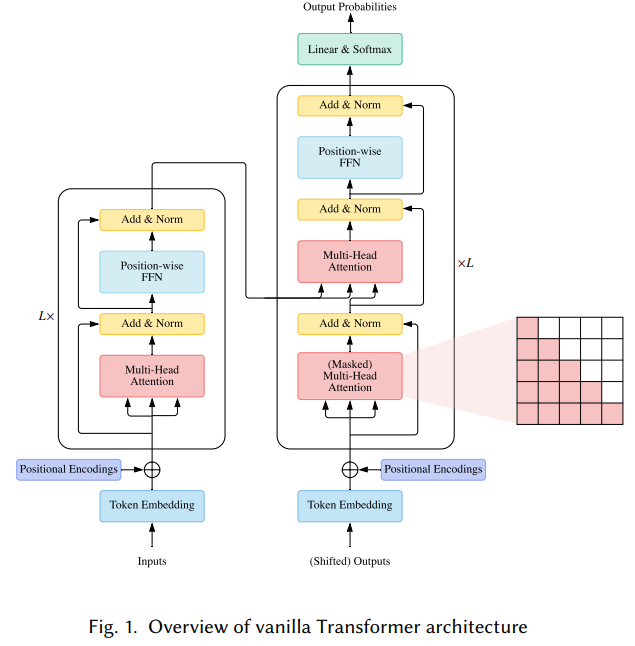
1) Attention Modules

Transformer는 Query-Key-Value(QKV) 모델로 동작하는 어텐션 메커니즘을 도입한다. 쿼리 벡터 Q

$Q\in \mathbb{R}^{N\times D_k}$, 키 벡터 $K\in \mathbb{R}^{M\times D_k}$ , 밸류 벡터 $V\in \mathbb{R}^{N\times D_v}$가 주어졌을 때, Transformer의 scaled dot-product attention 연산은 다음과 같다.

$Attention(Q, K, V) = {softmax(\frac{QK^T}{ \sqrt D_k}}) V$ $= AV$

Query (Q) : [참조 대상] 현재 단어에 대한 representation. 다른 단어와의 연관성을 계산할 때 질의 벡터 역할
Key (K) : [참조 소스] 각 단어의 representation. Query와 매칭하여 유사도를 계산. Query가 참조하는 대상 단어들의 키 벡터
Value (V) : [참조 값] 각 단어에 대한 값 벡터로, 최종적으로 Q에 반영될 가중치 정보. 어텐션 스코어에 따라 가중치 결정

$N$과 $M$은 쿼리와 키, 또는 밸류들의 길이를 나타낸다.

$D_k$는 키 벡터의 차원으로(내적을 위해 쿼리 벡터와 키 벡터의 차원은 동일함), $Q$, $K$의 내적에 $\sqrt D_k$를 나누는 것은 내적 값의 변화 정도를 안정화하여, softmax 함수의 gradient vanishing 문제를 완화하기 위함이다.

$D_v$는 밸류 벡터의 차원을 나타낸다. (일반적으로, $D_v ≥ D_k$)

$A$는 ${softmax(\frac{QK^T}{ \sqrt D_k}})$ 로, 어텐션 매트릭스(attention matrix)라고 부른다.

• Question. 입력값에 $\sqrt D_k$를 나누는 것이 어떻게 Softmax 함수의 gradient vanishing을 완화하는가?

Softmax 함수는 입력값들의 지수값을 계산 후 정규화 (0~1)하는 작업을 수행한다. 이 때, 입력값들의 범위가 너무 크면 지수값들 간 차이가 매우 커져서 gradient vanishing 문제가 발생할 수 있다.

$softmax(x)_i = \frac{e^{x_i}}{Σ_{j=1}^{K} e^{x_j}}$

예를 들어서, 입력값이 [$30, 20, 10$]일 때, 지수값은 대략 [$1.0686474581524×10^{13}$, $4.851651954097903×10^8$, $22026.465794806718$]으로, $e^{30}$의 값이 매우 커서 softmax 결과가 [$1, 0, 0$]에 가까워진다. 이렇게 작은 값들에 대한 gradient가 $0$에 수렴하여 제대로 업데이트되지 않는 gradient vanishing 문제가 발생한다.

반면, 입력값에 $\sqrt D_k$를 나누게 되면, 입력값의 범위가 감소하여 지수값 간 차이가 줄어든다.

예를 들어, $\sqrt D_k=5$라 할 때, $[30/5, 20/5, 10/5]$ = $[6, 4, 2]$가 되어 지수값들의 범위가 좁혀지고, softmax 결과값의 분포는 ≈$≈$$[0.70538451, 0.25949646, 0.03511903]$ 정도로 grdient vanishing 현상을 줄일 수 있다.

결과적으로, 내적값을 $\sqrt D_k$로 스케일링하게 되면 softmax 함수의 입력값 범위를 조절하여 gradient vanishing 문제를 완화하고, 작은 값의 gradient도 업데이트 할 수 있게 된다.

Transformer는 단순 어텐션 함수를 적용하지 않고 multi-head attention을 사용한다.

$D_m$차원의 query, key, value는 $H$(heads의 수)개의 서로 다른 학습된 projection 집합으로, 각각 $D_k$, $D_k$, $D_v$ 차원으로 projection된다. 각 projected query, key, value들의 출력은 식 (1)에 따라 어텐션으로 계산된다. 그 다음, 모델은 모든 출력을 연결(concatenate)하고 다시 $D_m$ 차원의 representation으로 projection한다.

→ 즉 multi-head attention은 query, key, value를 여러개의 subspace로 linearly projection하고 각 subspace에서 어텐션을 개별적으로 연산한 다음, 그 결과를 연결(concatenate)하여 최종 어텐션 값을 얻는다.

Transformer에는 3가지의 어텐션이 있다 : self-attention, masked self-attention, cross-attention

1. Self-attention
   : Transformer encoder에서 $Q = K = V = X$. $X$는 이전 레이어의 출력 입력 시퀀스 내 다른 위치에 있는 단어 간 의존성을 모델링한다. 각 단어가 모든 다른 단어와 어텐션 연산 수행을한다.

2. Masked self-attention (Decoders)
   : Transformer decoder에서 각 위치에 있는 쿼리가 해당 위치까지의 키-값 쌍에만 attend할 수 있도록 self-attention을 제한하여 병렬화를 가능하게 한다. 현위치에서 그 이후 위치의 토큰 정보를 masking한다. (e.g. 5번째 단어 생성 시, 1~4번째 단어만 고려하고 6번째부터 masking 적용 → masking : attention weight를 0으로 설정하는 것?). autoregressive 또는 casual attention 특성을 반영한 것.

3. Cross-attention (Decoders)
   : 쿼리는 이전 decoder 레이어의 출력에서, 키와 값은 encoder의 출력에서 가져온다. decoder에서 encoder의 출력을 참조하여 decoding 출력을 생성한다. (e.g. 기계 번역에서 소스 문장을 참조하여 타겟 문장 생성). encoder-decoder 구조에서 소스 시퀀스와 타겟 시퀀스 간 관계 학습에 사용한다. (타겟 시퀀스의 각 단어 생성을 위해 소스 시퀀스의 모든 위치에 attend 함)

• Question. unnormalized attention matrix에 mask function을 적용하여 illegal positions를 masking하는 것이 왜 병렬화를 가능하게 하는가?

일반적인 sequence data를 처리할 때는 이전 시점 출력이 다음 시점 입력이 되므로, 순차적으로 계산하여야 한다. 그러나, Transformer의 self-attention은 이론적으로 모든 위치에 대해 동시에 계산하는 것이 가능하다.

그러나, decoder에서는 autoregressive 특성 때문에, 각 위치에서 해당 위치 이후의 정보를 참조하면 안 된다. 이러한 특성을 지키기 위해 attention score matrix에서 illegal position에 masking을 한다. 이렇게 masking을 하면 각 위치 출력이 해당 위치 이후 정보에 영향받지 않게 되므로, 모든 위치 출력을 동시에 계산할 수 있어 병렬화가 가능해진다.

만약, 마스킹 없이 순차적으로 계산하면, 이전 위치 계산 결과가 나와야 다음 위치를 계산할 수 있으므로 병렬화가 어렵다. 결과적으로, masking 작업을 통해 autoregressive 특성을 지키면서, 전체 시퀀스에 대한 계산을 병렬 수행할 수 있게 되어 학습 및 추론 속도가 빨라지는 것이다.

autoregressive : sequence modeling에서 현재 시점의 출력이 과거 시점의 입력에만 의존해야 한다. 현재 단어를 예측할 때 앞서 나온 단어만 참조하여, 미래 정보가 현재 예측에 영향을 주는 것을 방지한다.

2) Position-wise FFN

position-wise FFN은 각 position에서 개별적으로 동일하게 작동하는 fully connected feed-foward 모듈이다.

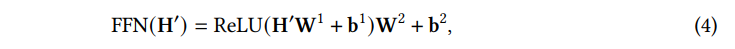
여기서 $H’$는 이전 레이어의 출력, $W^1 ∈ \mathbb{R}^{𝐷_𝑚×𝐷_𝑓}$, $W^2 ∈ \mathbb{R}^{𝐷_𝑓 ×𝐷_𝑚}$, $b^1 ∈ \mathbb{R}^{𝐷_𝑓}$, $b^2 ∈ \mathbb{R}^{𝐷_m}$는 훈련 가능한 파라미터들이다. 일반적으로 FFN의 $D_f$ (hidden layer의 차원 수)는 $D_m$ (FFN 의 입,출력 차원 수) 보다 크게 설정한다. [→ 높은 차원의 hidden layer를 거쳐 입력을 더 expressive한 표현 공간에 projection 하기 위함]

3) Residual Connection and Normalization

Transformer는 deep model 구축을 위해 각 모듈 주변에 residual connection을 사용하고, 그 뒤에 Layer Normalization을 수행한다.

예를 들어, 각 Transformer의 encoder block은 다음과 같이 표현될 수 있다.

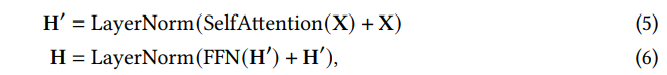
여기서 $SelfAttention(·)$은 self attention 모듈을, $LayerNorm(·)$은 layer normalization 연산을 나타낸다.

4) Position Encodings

Transformer는 순환 신경망(recurrence)이나 컨볼루션(convolution)을 사용하지 않으므로, positional information를 인식하지 못한다(특히 encoder에서, 입력 시퀀스 각 토큰이 시퀀스 내에서 어떤 위치에 있는지 알 수 없음). 따라서, 토큰 순서를 모델링하기 위해서는 positional representation이 추가로 필요하다.

---

Model Usage

일반적인 Transformer 구조는 다음 3가지 방법으로 활용된다.

1. Encoder-Decoder
   : full Transformer architecture. 기계번역과 같은 sequence-to-sequence modeling에 사용

2. Encoder only
   : encoder만 사용, encoder의 출력을 입력 시퀀스의 representation으로 사용. classification이나 sequence labeling에서 사용

3. Decoder only
   : decoder만 사용. encoder-decoder cross-attention 모듈을 제거하고 사용. 일반적으로 language modeling과 같은 sequence generation에 사용

---

Model Analysis

Transformer의 computation time과 parameter requirement를 설명하려면, Transformer의 핵심 컴포넌트인 self attention과 point-wise FFN에 대해 분석해야 한다.

모델의 hidden dimension $D_m$을 $D$라고 가정하고, 입력 시퀀스 길이를 $T$라고 가정해 보자.

Transformer 논문에 따르면, FFN의 중간 은닉층 차원은 $4D$로 설정되며, key와 value의 차원은 $D/H$로 설정된다.

Transformer의 계산 복잡도는 입력 시퀀스의 길이와 모델 차원에 따라 달라진다. 입력 시퀀스가 짧으면, FFN의 complexity가 $O(TD^2)$로 hidden dimension $D$가 주요 병목 지점이 된다.

그러나 입력 시퀀스 길이 $T$가 길어질수록, self-attention 연산의 complexity $O(T^2D)$가 점차 지배적이 되고, 이 경우 self-attention이 주요 병목 지점이 된다. (모든 쌍에 대한 어텐션 스코어를 계산해야 하기 때문에 $T^2$에 비례하는 연산이 필요)

더불어, self-attention 연산에는 $T\times T$ 크기의 attention distribution matrix를 저장해야 하므로, 긴 시퀀스 시나리오 (예를 들어, 긴 텍스트 문서, 고해상도 이미지의 픽셀 단위 모델 등)에서는 Transformer 연산을 실현하는 것이 어려워진다.

결국, Transformer의 효율을 향상시키려면 일반적으로 (1) self-attention의 긴 시퀀스에 대한 호환성 향상과, 일반적인 상황에서 (2) position-wise FFN의 연산 및 파라미터 효율성을 향상시켜야 한다는 것이다.

• FFN 모듈 구조

Input ($d_{model}$ 차원) -> Linear ($d_{ff}$ 차원) -> ReLU -> Linear ($d_{model}$ 차원) -> Output
$d_{ff}$ → intermediate dimension (FFN 모듈의 중간 은닉층)

---

Comparing Transformer to Other Network Types

Self-attention analysis

Transformer의 중심 구성요소인 self-attention은 가변 길이 입력을 처리할 수 있는 flexible mechanism을 제공한다. self-attention은 입력 간 pairwise 관계에서 동적으로 가중치가 생성되는 완전연결층이라고 할 수 있다.

아래 Table 2는 셀프 어텐션의 복잡도(Complexity), 순차 연산(Sequential Operations), 최대 경로 길이(Maximum Path Length)를 세 가지 일반적인 layer type과 비교한다.

비교 결과, self-attention의 장점은 다음과 같이 요약 할 수 있다:

(1) 완전연결층(Fully Cnnected)과 동일한 maximum path length를 가지므로, long-range dependencies modeling(장거리 의존성 모델링)에 적합하다. 완전연결층에 비해 파라미터 효율성이 높고 가변 길이 입력 처리에 유연하다.

(2) Convolutional layer는 receptive field가 제한되어, global receptive field를 가지려면 일반적으로 네트워크를 깊게 쌓아야 한다. 반면, self-attention의 maximum path length는 일정하므로 고정된 수의 층으로도 장거리 의존성을 모델링할 수 있다.

(3) self-attention은 sequential operation과 maximum path length이 일정하므로, 병렬처리가 가능하고 Recurrent layer보다 장거리 모델링에 적합하다.

Inductive Bias

• Question. What is Inductive Bias? (귀납적 편향)
  

머신 러닝 모델이 훈련 데이터로부터 어떻게 일반화를 수행할 것인지에 대한 가정.

즉, 모델이 학습 데이터 외의 새로운 데이터에 대해 예측을 할 때, 어떤 패턴이나 구조를 선호하는지를 나타내는 경향성이다. 모델 구조, 정규화 기법, 손실함수 등이 모델의 inductive bias를 결정하게 된다.

이러한 bias는 모델의 일반화 성능과 학습 속도를 향상시킬 수 있지만, 잘못된 가정은 성능 저하로 이어질 수 있으므로 적절한 trade-off를 찾는 것이 중요하다.

Transformer를 Convolution이나 Recurrent Network와 비교해볼 수 있다. Convolutional Network는 local kernal functions를 통해, translation invariance와 locality에 대한 inductive bias를 부여한다.

이와 유사하게, Recurrent network는 Markovian structure를 통해, 일시적인 invariance와 locality에 대한 inductive bias를 갖게 된다.

반면, Transformer 구조는 데이터의 structural information에 대한 assumption이 거의 없고, 이를 통해 범용적이고 flexible한 architecture가 된다. 이에 대한 부작용으로, Transformer는 structural bias가 부족하여 소규모 데이터에서 overfitting되기 쉽다.

메세지 전달을 기반으로 하는 Graph Neural Networks(GNNs)와 Transformer를 비교해 보면, Transformer는 각 입력이 그래프의 노드가 되는 ‘complete directed graph (with self-loop)’ 에 정의된 GNN이라고 볼 수 있다. Transformer와 GNN의 큰 차이점은, Transformer는 입력 데이터가 어떻게 구조화되었는지에 대한 사전 지식을 도입하지 않는다는 것이다. Transformer의 메시지 전달 프로세스는 전적으로 내용의 유사도에 달려있다.

[참고] Inductive bias of CNN

• Locality
  : kernel 연산을 통해 local receptvie field만 고려하므로, 각 뉴런은 입력 데이터의 일부 영역만 참조하여 계산된다. (→ Assumption : 실제 이미지 데이터에서 중요한 특징들은 지역적으로 군집되어 있다)

• Translation invariance
  : kernel weight가 입력 전체에 공유된다. 동일한 특징이 이미지 어디서 나타나도 동일한 kernel로 추출할 수 있다 (→ Assumption : 객체가 이미지 내 어디에 위치하여도 동일 객체로 인식되어야 한다