지난번 시계열 예측 포스팅에는 모델을 돌려보고 단순하게 결과를 확인하는 수준에서 그쳤는데, 시계열 관련 강의나 공부를 더 하고 나서 보니 도출 과정이나 시각화 부분이 부족한 것 같아서 삼성전자 주가 예측을 다시 해보려고 한다.
지난번에는 ARIMA 모델과 LSTM을 적용하여 예측했지만, 이번에는 ARIMA, SARIMA 모델을 활용해 보려고 한다. SARIMA는 ARIMA에 seasonal 요소를 추가한 모델이다.
여담으로 실습에 참고했던 김성범 교수님의 유튜브 실습 강의에서는 주가 예측 같은 경우 SARIMA보다는 ARIMA를 활용하는 게 좋을것 같다고 한다. (주가 예측에서는 seasonal이 강하지 않아서?)
0. 모듈 임포트
import os
import pandas as pd
import pandas_datareader.data as pdr
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
import matplotlib.pyplot as plt
import matplotlib
%matplotlib inline
import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima_model import ARIMA
from statsmodels.tsa.statespace.sarimax import SARIMAX
from pmdarima.arima import auto_arima
import seaborn as sns
plt.style.use('seaborn-whitegrid')
import itertools
import warnings
warnings.filterwarnings('ignore')pandas_datareader, pmdarima 라이브러리 같은 경우 pip install을 해주어야 한다
1. 데이터 로드 / 확인
import yfinance as yf
df = yf.download('005930.KS',
start='2022-01-01',
end='2022-05-12') # 005930 : 삼성전자 주가
df.head()지난번과 동일하게 yfnance 라이브러리를 통해 삼전 주가를 로딩해 온다. 내가 선택한 기간은 2022년 1월부터 포스팅 날짜 이전까지. 주가 같은 경우에는 짧은기간의 변동폭이 커서 오랜 기간을 불러오면 예측 성능이 떨어지는 것 같다. (실제로 17년도부터 불러와서 예측을 해 본 결과, 예측이 완전 빗나감을 확인했다 😥)
fig = df['Close'].plot()예측 대상은 종가이므로, 종가를 시각화 해 본다.
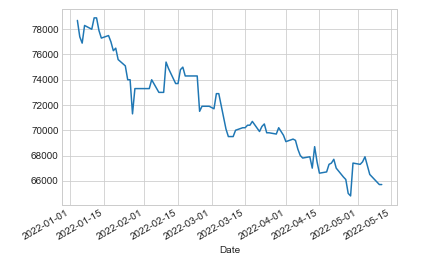
2022-01-01 ~ 2022-05-12 날짜에 해당하는 삼성전자 종가 그래프가 다음과 같이 그려진다.
2. decomposition
decompostion이란, 시계열 데이터를 시계열 4요소(추세, 순환, 계절, 불규칙)으로 분해하는 기법이다.
추세(Trend)
데이터가 장기적으로 증가하거나 감소하는 것순환(cycle)
정치, 경제, 사회적 요인에 대한 변화로, 장기적인 변화 현상계절(seasonal)
특정 주기로 나타나는 패턴(주, 월, 분기 등)불규칙(random)
설명할 수 없고 예측이 불가능한 임의의 변동
statsmodels.tsa 에서 seasonal_decompose를 사용하여 decompostion 결과를 확인할 수 있다.
# seasonal decomposition
decomposition = sm.tsa.seasonal_decompose(df['Close'], model='additive', period=1)
fig = decomposition.plot()
fig.set_size_inches(10, 10)
plt.show()model='additive'를 적용하여 덧샘 분해를 적용한다. (분해법에는 additive와 multiplicative가 있다)
- 덧셈 분해(additive decomposition)
- 곱셈 분해(multiplicative decomposition)
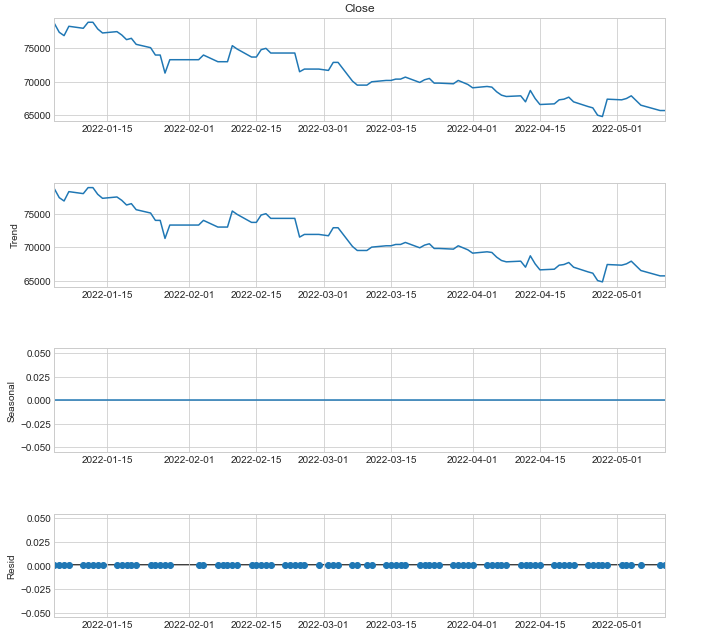
3. 자기상관함수(ACF), 부분자기상관함수(PACF)
시계열 데이터의 예측을 위해서는 데이터가 stationary인지, non-stationary인지 확인하는 절차를 거쳐야 한다.
따라서 ACF, PACF 플롯을 시각화하여 stationary 여부를 확인하고, non-stationary 일 경우 차분(difference)을 진행한다.
# split 8 : 2
train_data, test_data = train_test_split(df, test_size=0.2, shuffle=False)# ACF, PACF plot
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
fig.suptitle('Raw Data')
sm.graphics.tsa.plot_acf(train_data['Close'].values.squeeze(), lags=20, ax=ax[0])
sm.graphics.tsa.plot_pacf(train_data['Close'].values.squeeze(), lags=20, ax=ax[1])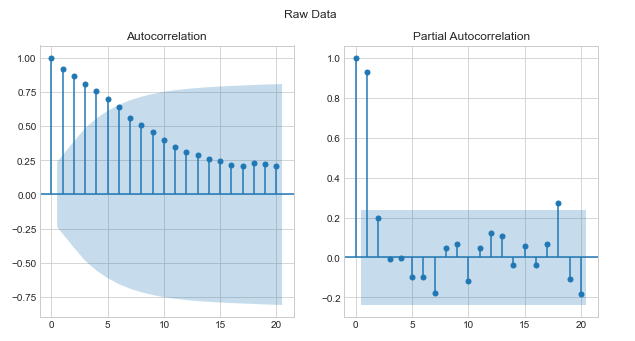
4. 차분(Differencing)
plot을 확인한 결과, ACF이 천천히 감소하는 패턴 -> non-stationary 이므로 차분을 진행한다.
# Non-stationary -> stationary 보정 (차분, difference)
# differencing
diff_train_data = train_data.copy()
diff_train_data = diff_train_data['Close'].diff() # 차분
diff_train_data = diff_train_data.dropna() # 차분 후 생기는 결측치 제거
print(f'{star*15}Raw data{star*15}')
print(train_data['Close'].head())
print(f'{star*15}Differenced data{star*15}')
print(diff_train_data.head())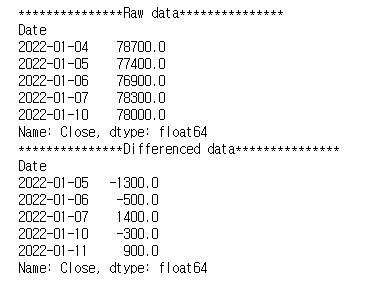
차분 전, 후를 비교하여 시각화 해 본다.
# 차분 시각화
fig = plt.figure(figsize=(12, 8))
ax1 = fig.add_subplot(2, 1, 1)
ax2 = fig.add_subplot(2, 1, 2)
ax1.plot(train_data['Close'])
ax1.legend('Raw data (Non-stationary)')
ax2.plot(diff_train_data, color='orange' )
ax2.legend('Differenced data (stationary)')
plt.tight_layout()
plt.show()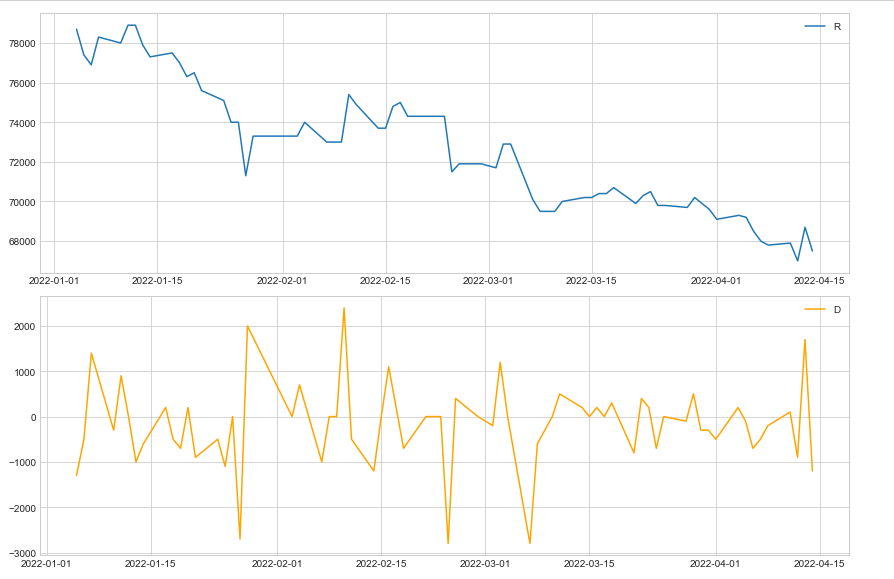
# ACF, PACF plot
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
fig.suptitle('Raw Data')
sm.graphics.tsa.plot_acf(diff_train_data.values.squeeze(), lags=20, ax=ax[0])
sm.graphics.tsa.plot_pacf(diff_train_data.values.squeeze(), lags=20, ax=ax[1])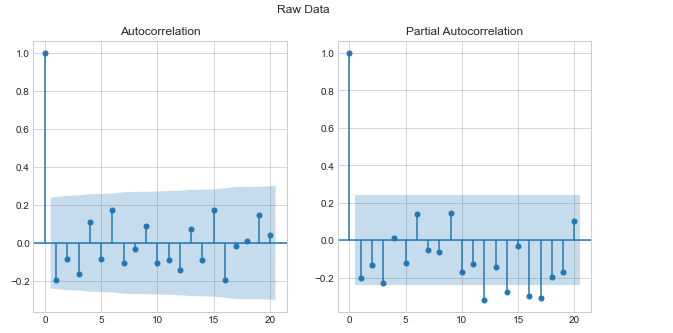
5. Diagnosis
ARIMA 모델을 적용할 때 최적 파라미터(q, d, p)를 탐색한다
# 최적 파라미터 서치
p = range(0, 2)
d = range(1, 3)
q = range(0, 2)
pdq = list(itertools.product(p, d, q))
AIC = []
for i in pdq :
model = ARIMA(train_data['Close'].values, order=(i))
model_fit = model.fit()
print(f'ARIMA pdq : {i} >> AIC : {round(model_fit.aic, 2)}')
AIC.append(round(model_fit.aic, 2))
AIC가 가장 적어지는 파라미터를 선택하면 된다.
# optimal paramter
optim = [(pdq[i], j) for i, j in enumerate(AIC) if j == min(AIC)]
print('Found Optimal Parameter :',optim)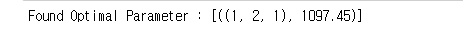
model = ARIMA(train_data['Close'].values, order=(1, 2, 1))
model_fit = model.fit()
model_fit.summary()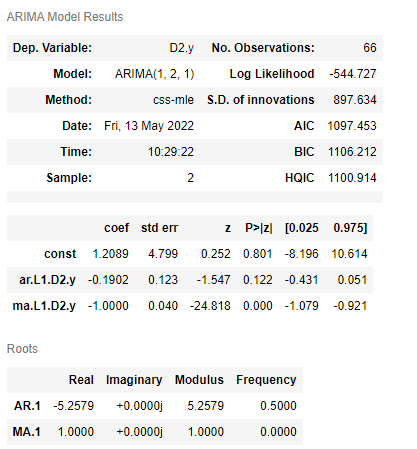
6. Forecasting with ARIMA
pred = model_fit.forecast(len(test_data))
pred_val = pred[0]
pred_ub = pred[2][:, 0]
pred_lb = pred[2][:, 1]
pred_index = list(test_data.index)
r2 = r2_score(test_data['Close'].values, pred_val)fig, ax = plt.subplots(figsize=(12, 6))
df['Close'].plot(ax =ax)
ax.vlines('2022-04-15', 60000, 80000, linestyle='--',color='r', label='Start of Forecast')
ax.plot(pred_index, pred_val, label='Prediction')
ax.fill_between(pred_index, pred_lb, pred_ub, color='k', alpha=0.1, label='0.95 pred Interval')
ax.legend(loc='upper left')
plt.suptitle(f'ARIMA {optim[0][0]} Pred Result R^2 score : {round(r2, 2)}')
plt.show()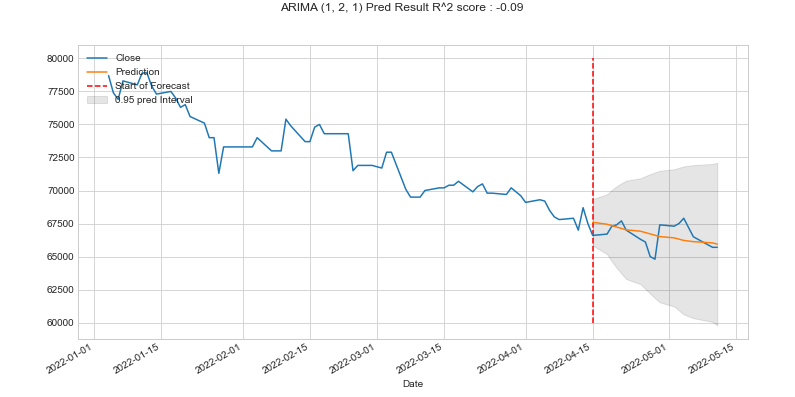
8:2로 split 하여 4월 15일부터의 데이터를 예측한다. 노란색이 예측, 파란색이 실제 종가이다.
전체적인 감소 추세는 얼추 비슷한데, 예측 정확도는 그렇게 좋지 않아 보인다.
7. Diagnosis - SARIMA
sarima 모델의 최적 하이퍼파라미터를 탐색한다.
# parameter search
p = range(0, 3)
d = range(1, 2)
q = range(0, 3)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], 3) for x in pdq]
AIC = []
params = []
for i in pdq :
for j in seasonal_pdq :
try :
model = SARIMAX(train_data['Close'].values, order=(i), seasonal_order = (j))
model_fit = model.fit()
print(f'SARIMA : {i},{j} >> AIC : {round(model_fit.aic, 2)}')
AIC.append(round(model_fit.aic, 2))
params.append((i, j))
except Exception as e:
print(e)
continueARIMA의 탐색 과정에 seasonal_pdq를 추가하면 된다.
# optimal parameter
optim = [(params[i], j) for i, j in enumerate(AIC) if j == min(AIC)]
print(optim)8. Forecasting with SARIMAX
같은 데이터에 SARIMAX 모델을 적용해 본다.
model = SARIMAX(train_data['Close'].values, order=optim[0][0][0], seasonal_order=optim[0][0][1])
model_fit = model.fit()
model_fit.summary()앞서 탐색한 최적 파라미터를 사용하여 모델을 피팅한다.
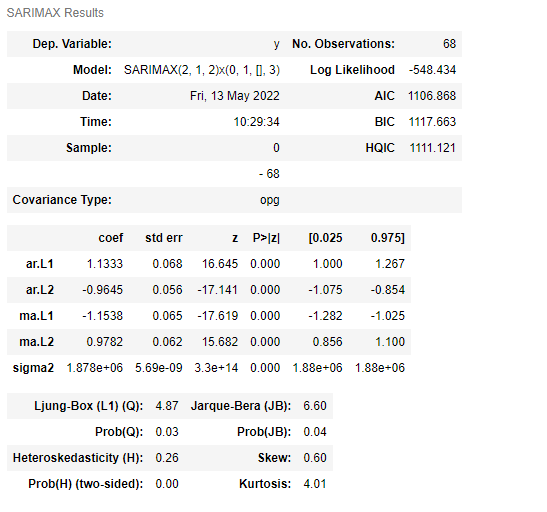
AIC가 1097 -> 1106으로 ARIMA에 비해 결과가 좋아지진 않은 것으로 보인다.
앞선 ARIMA와 같은 방식으로 예측 결과를 시각화 해 본다.
pred = model_fit.get_forecast(len(test_data))
pred_val = pred.predicted_mean
pred_ub = pred.conf_int()[:, 0]
pred_lb = pred.conf_int()[:, 1]
pred_index = list(test_data.index)
r2 = r2_score(test_data['Close'].values, pred_val)fig, ax = plt.subplots(figsize=(12, 6))
df['Close'].plot(ax =ax)
ax.vlines('2022-04-15', 60000, 80000, linestyle='--',color='r', label='Start of Forecast')
ax.plot(pred_index, pred_val, label='Prediction')
ax.fill_between(pred_index, pred_lb, pred_ub, color='k', alpha=0.1, label='0.95 pred Interval')
ax.legend(loc='upper left')
plt.suptitle(f'SARIMA {optim[0][0]} Pred Result R^2 score : {round(r2, 2)}')
plt.show()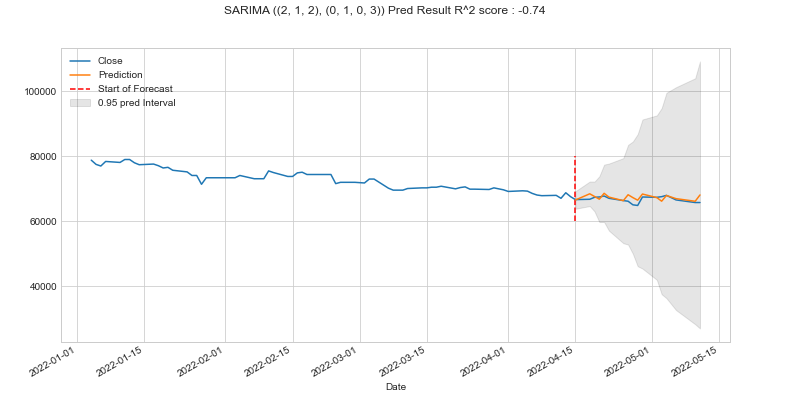
AIC로 보면 결과가 그리 좋지 않을 것으로 보였는데..
곡선 형태로 보면 ARIMA보다 더 잘 예측한 것으로 보인다.
9. auto ARIMA
마지막으로 auto ARIMA를 활용해서 최적 파라미터를 자동으로 탐색하고 적용해 본다.
auto_arima_model = auto_arima(train_data['Close'], start_p=1, start_q=1,
max_p=3, max_1=3, m=3, seasonal=True, # sarima(seasonal=True)
d=1, D=1,
max_P=3, max_Q=3,
trace=True,
error_action='ignore',
suppress_warnings=True,
stepwise=False)
auto_arima_model.summary()seasonal = True option을 주는 경우 sarima와 같은 결과를 얻을 수 있다. arima를 적용하고 싶은 경우는 False를 주면 된다.
pred = auto_arima_model.predict(len(test_data), return_conf_int=True)
pred_val = pred[0]
pred_ub = pred[1][:,0]
pred_lb = pred[1][:,1]
pred_index = list(test_data.index)
r2 = r2_score(test_data['Close'].values, pred_val)fig, ax = plt.subplots(figsize=(12, 6))
df['Close'].plot(ax =ax)
ax.vlines('2022-04-15', 60000, 80000, linestyle='--',color='r', label='Start of Forecast')
ax.plot(pred_index, pred_val, label='Prediction')
ax.fill_between(pred_index, pred_lb, pred_ub, color='k', alpha=0.1, label='0.95 pred Interval')
ax.legend(loc='upper left')
plt.suptitle(f'auto_ARIMA {optim[0][0]} Pred Result R^2 score : {round(r2, 2)}')
plt.show()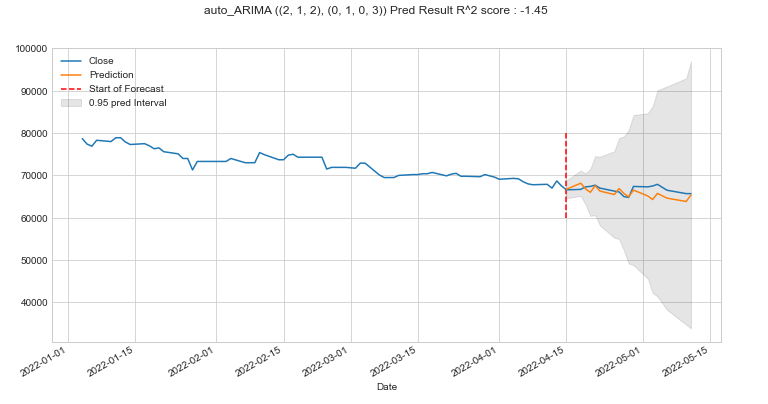
auto arima의 결과는 위와 같다. 앞서 한 최적 파라미터 서치 과정을 자동으로 수행해 주어서 아주 편리하다!!
이렇게 ARIMA, SARIMA 모델을 적용하고 시각화도 해 보았는데, 다음엔 다변량 시계열 예측도 진행해 보아야겠다.
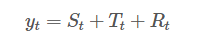
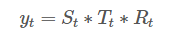

안녕하세요 시계열 모델로 데이터 예측하려고 공부하고 있습니다. 좋은 정보 정말 감사합니다. 혹시 다른 시계열 모델로 추가로 하신 거 있으시면 공유 가능하실까요?