
AI 모델 논문들을 보다 보면, Training Objective에 KL divergence 개념이 많이 언급된다. 요즘 공부하고 있는 diffusion이나 VAE에서도 중요한 개념으로, 오늘은 이 KL divergence에 대해 수식적으로 정리해보려고 한다.
KL-divergence란?
KL-Divergence (쿨백 라이블러 발산)은 기준 확률 분포와 다른 분포의 차이를 측정하는 지표이다.
로 표현하며, 를 기준으로 와의 차이를 측정한다는 의미이다. KL-Divergence 연산 식에서는 를 분포로 근사할 때 발생하는 정보 손실을 측정하게 된다.
연속확률분포(continuous) P, Q에 대한 KL divergence
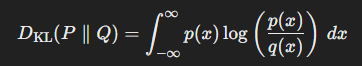
- , 는 연속 확률 변수 에 대한 , 의 확률 밀도 함수(PDF)
- 적분을 통해 x의 모든 값에 대한 , 간 비율을 계산
이산확률분포(discrete) P, Q에 대한 KL divergence
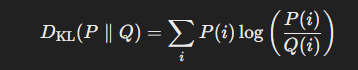
- , 는 이산 확률 변수 에 대한 , 의 확률값
- 이산확률분포에서는 각 i에 대해 확률 비율 을 계산하고, 이 비율에 대한 로그값을 로 가중하여 합산
(예시) 두 가우시안 분포의 KL-divergence
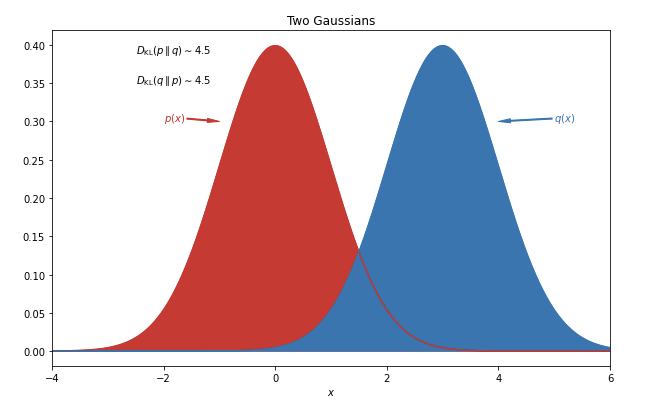
두 가우시안 분포 $ p(x), q(x)$에 대한 KL-divergence는 다음과 같이 계산할 수 있다.
, 일 때, 가우시안 분포의 PDF는 다음과 같다.
,
따라서 는 다음과 같이 계산된다.
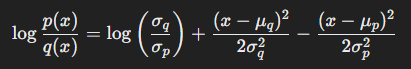
위 표현을 적분식에 대입하여 계산하면, 두 가우시안 분포의 KL-divergence는 다음과 같이 정리된다.
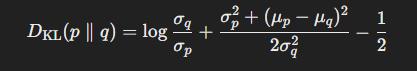
AI Model에서 KL-divergence objective
KL-Divergence는 확률기반 모델 학습, 특히 분류나 생성 모델에 실제 데이터 분포를 근사시키기 위한 optimization objective로 많이 사용된다. (VAE, diffusion, etc.) 모델은 KL-divergence를 최소화하여 실제 데이터 분포 와 모델 분포 간의 차이를 줄이는 방향으로 학습한다.
KL-divergence in Diffusion Model
Diffusion Model의 학습 과정은 크게 (1) 원본 데이터 분포에 점진적으로 노이즈를 추가하여 노이즈 분포로 변환하는 forward process와, (2) 노이즈 분포를 원래 데이터 분포로 복원하는 reverse process로 구성되어 있다. (이 포스팅에서 diffusion model 자체에 대해 자세히 다루진 않겠다)
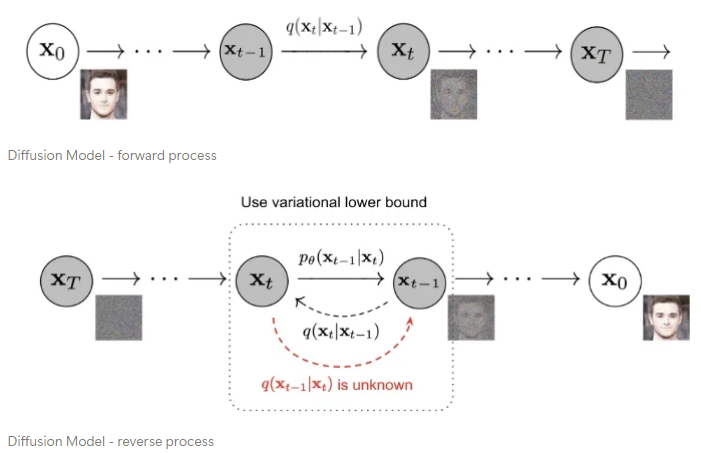
Diffusion 모델의 목표는 모델이 학습한 reverse process 와 실제 데이터 분포의 forward process 간의 차이를 최소화하는 것이다. 이 차이를 KL-divergence를 사용해 측정하고, 이를 최소화하는 것이 모델의 학습 목표가 된다(ELBO; Evidence Lower Bound).
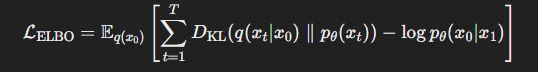
KL-divergence는 각 time step 에서 모델이 학습한 분포와 실제 데이터 분포의 차이를 측정하고 이를 최소화함으로써, 데이터에서 점진적으로 노이즈를 제거해 원래 데이터 분포로 복원하는 과정을 거친다. 이러한 복원 과정을 통해 모델은 정확한 분포를 학습할 수 있게 된다.
