Single Random Variables and Probability Distributions
Random variable(확률변수)
확률 실험의 실험 결과나 사건을 sample space에서 실수축의 한 점으로 mapping시키는 함수이다.
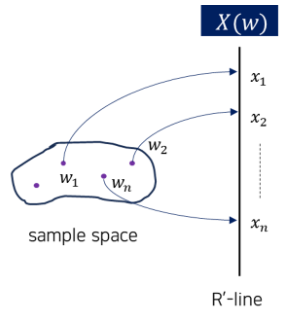
- 확률 변수의 종류
- Discrete random variable (이산확률변수)
: “countable”한 값만을 포함하는 확률 변수 (e.g. 주사위 확률, 동전 확률)
- Continuous random variable (연속확률변수)
: 특정 구간 내의 값을 포함하는 확률 변수 (e.g. 0부터 1까지의 랜덤 값)
- Mixed random variable (혼합확률변수)
: 이산 확률과 연속 확률이 혼재되어 있는 확률 변수
Probability Distribution Functions
1. Cumulative Distribution Function (누적분포함수)
연속확률변수 X에 대한 cdf는 다음과 같의 정의된다.
FX(x)=P(X≤x)
- CDF의 성질
-
모든 cdf는 x가 감소할수록 0에 가까워지고, 증가할수록 1에 가까워진다.
limx→−∞FX(x)=0 , limx→∞FX(x)=0
FX(−∞)=0 , FX(∞)=1
-
모든 cdf는 단조 비감소 함수(monotone non-decreasing)이다.
즉, x2≥x1 이면, FX(x2)≥FX(x1)
-
모든 cdf는 우측으로부터의 연속성을 가진다.
FX(x0)=limx→x0+FX(x)
-
X값이 x1과 x2사이에 있을 확률은 다음과 같이 표현된다.
P(x1≤X≤x2)=FX(x2)−FX(x1)
2. Probability Density Function (확률밀도함수)
연속확률변수 X에 대한 pdf는 다음과 같이 표현된다.
fX(x)=dxdFX(x)
도함수의 정의를 이용하면, pdf를 다음과 같이 표현할 수 있다.
fX(x)=limΔx→0 ΔxFX(x+Δx)−FX(x)
Δx가 충분히 작으면, lim을 제거하고 다음과 같이 표현할 수 있다.
FX(x+Δx)−FX(x)=P(x<X≤x+Δx)=fX(xΔx)
- pdf의 성질 확률변수 X에 대한 pdf fX(x)는 cdf FX(x)의 도함수이다. 또한, cdf FX(x)는 pdf fX(x)의 적분으로 표현될 수 있다. (미분-적분의 관계) 즉, FX(X)=∫−∞xfX(u)du
- pdf는 non-negative function이다. (→ cdf가 non-decreasing 함수이기 때문에, cdf의 도함수인 pdf 또한 non-negative이다.) 즉, fX(x)≥0
- pdf를 전 구간에 걸쳐 적분하였을 때 그 값이 1이다. (→FX(∞)=1) ∫−∞∞fX(x)dx=1
- x1과 x2 사이에 X값이 포함될 확률은 다음과 같이 표현된다. P(x1<X≤x2)=∫x1x2fX(x)dx =FX(x2)−FX(x1)=∫−∞x2fx(u)du−∫−∞x1fx(u)du=∫x1x2fX(u)du
cdf, pdf of Discrete Random variable
이산확률변수의 cdf는 weighted and shifted unit step function u(x)의 합으로 표현될 수 있다.
FX(x)=∑i=1Npiu(x−xi)
마찬가지로, 이산확률변수의 pdf fX(x)는 weighted and shifted unit impulse function δ(x)의 합으로 표현될 수 있다.
fX(x)=∑i=1Npiδ(x−xi)
Continuous random variable and their Distribution Functions
(연속확률변수와 그 분포함수)
균등분포의 pdf는 다음과 같다.
fX(x)={(b−a)10a≤x≤b, b>aotherwise
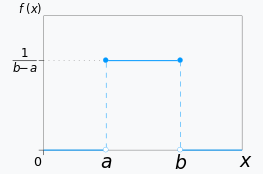
균등분포의 cdf는 다음과 같다.
FX(x)=⎩⎪⎨⎪⎧0b−ax−a1a≤x≤b,b>aa<x≤bx>b
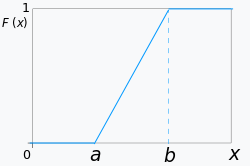
2. Gaussian Random Variable
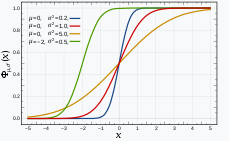
가우시안 분포의 pdf는 다음과 같다.
fX(x)=2πσ2e(x−m)2/2σ2
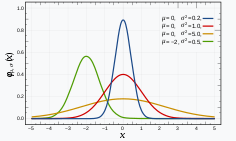
가우시안 분포의 cdf는 적분으로 직접 구하기 어려워, Q 함수(또는 error 함수)를 사용하여 표현한다.
FX(x)=1−Q(σx−m)
Q함수의 정의
Q(x)=2π1∫x∞e−u2/2du
error 함수(오차함수)의 정의
erf(x)=π2∫0xe−u2du
3. Exponential Random Variable
지수 분포의 pdf
fX(x)=αe−αxu(x), α>0
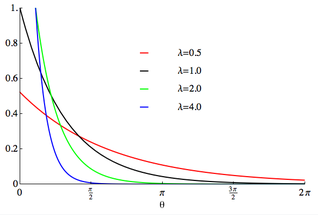
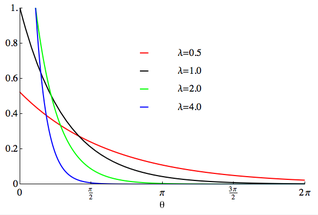
지수 분포의 cdf
FX(x)=(1−e−αx)u(x)
4. Gamma Random Variable
감마 분포의 pdf는 다음과 같다.
fX(x)=Γ(b)cbxb−1e−cxu(x), b,c>0
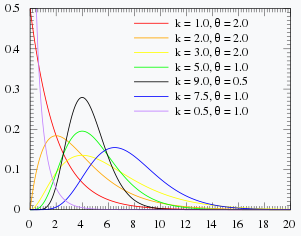
Γ(b)=∫0∞yb−1e−ydy
- Chi-square pdf
fX(x)=2n/2Γ(n/2)1x(n/2)−1e−x/2u(x)
- Erlang pdf
fX(x)=(n−1)!cnxn−1e−cxu(x)
5. Cauchy Random Variable
fX(x)=x2+α2α/π
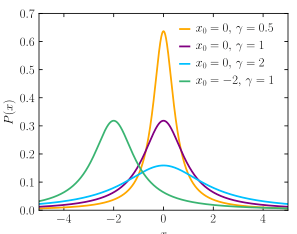
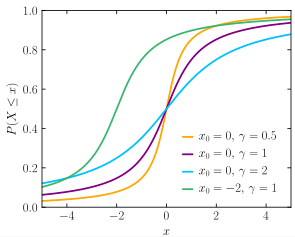
FX(x)=21+π1tan−1αx
Discrete random variable and their Distribution Functions
(이산확률변수와 그 분포함수)
1. Binomial Random Variable
이항 분포
P(X=k)=(kn)pkqn−k, k=0,1,2,…,n
where p+q=1
fX(x)=∑k≤xn(kn)pkqn−kδ(x−k)
FX(x)=∑k≤x(kn)pkqn−k
2. Geometric Random Variable
기하 분포는 k번째 시도에서 첫 번째로 성공할 확률에 대한 분포이다.
P(first success at trial k)=P(X=k)=(1−p)k−1p, k=1,2,…
3. Poisson Random Variable
포아송 분포
P(X=k)=k!ake−a, k=0,1,2,…
fX(x)=∑k=0∞k!ake−aδ(x−k)
FX(x)=∑k=0∞k!ake−au(x−k)
- **Poisson Point** 임의의 구간 T에서 k개의 사건이 발생할 확률 P(X=k)=k!(λT)ke−λT, k=0,1,2,… 이 때, λ 는 단위 시간당 발생하는 사건의 수 fW(w)=λe−λwu(w) FW(w)=P(W≤w)=1−P(X=0)=1−e−λw, w≥0
De Moivre-Laplace Theorem(드므와브르-라플라스 정리)
n 크기가 충분히 크다면, 이항분포를 가우시안 분포로 근사할 수 있다.
pkqn−k≈2πσ2e−(k−m)2, n>>1
드므와브르-라플라스 정리에 근거하여 이항분포의 cdf 또한 다음과 같이 근사된다.
FX(x)≈1−Q(npqx−np)
4. Pascal Random Variable
일련의 베르누이 시행에서 k번 성공하기까지 실행 횟수에 대한 분포
P=(X=k)=(k−1n−1)pkqn−k, k=1,2,…, q=1−p
5. Hypergeometric Random Variable
N개의 모집단에서 n개의 샘플을 무작위로 뽑았을 때 성공 횟수에 대한 분포 (K→ 모집단 성공 횟수, k→샘플 중 성공 횟수)
P(X=k)=(nN)(kK)(n−kN−K), k=0,1,2,…,n











