참조: https://www.youtube.com/watch?v=LFMrrTqqt4M&t=154
참조: http://contents2.kocw.or.kr/KOCW/document/2015/pukyong/kwonoeum/6.pdf
참조: https://code-lab1.tistory.com/13
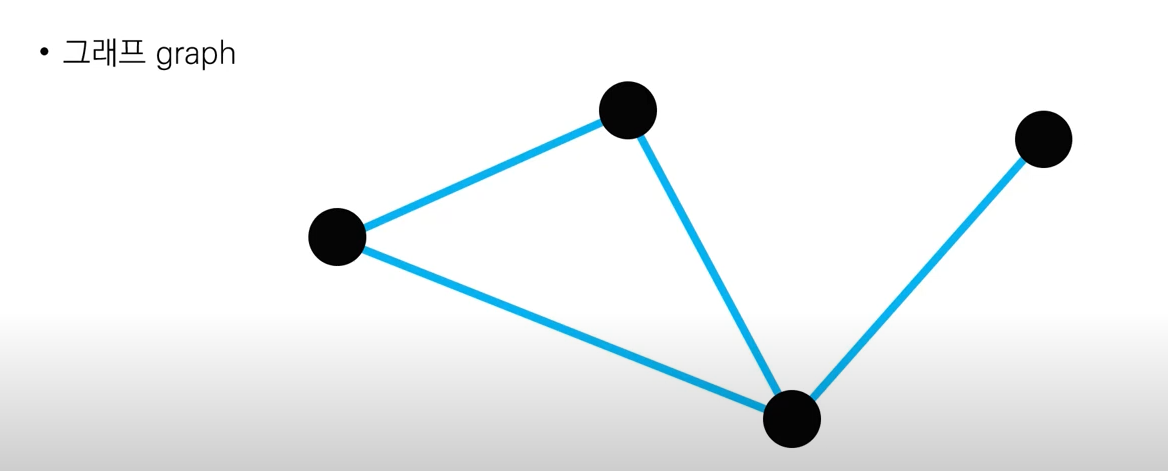
1. 그래프란?
그래프(Graph): 정점과 간선으로 이루어진 구조를 나타내는 수학적인 개념 (G = (V, E))
- 정점(Vertex): 그래프에서 하나의 점을 나타낸다. 데이터를 저장하는데 사용될 수 있다.
- 간선(Edge): 정점과 정점을 연결하는 선. 정점 쌍 사이의 관계를 나타낸다.
단순 그래프(Simple Graph): '루프'와 '다중 간선'이 없는 그래프
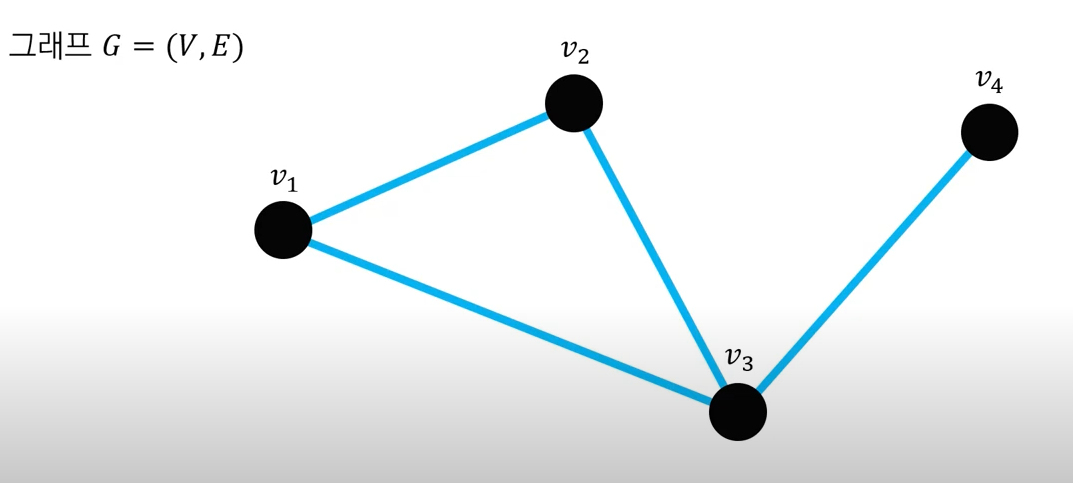
- 이 그래프에서는 4개의 정점과 4개의 간선으로 이루어진 그래프이다.
- V = V(G) = {v1, v2, v3, v4}
- E = E(G) = {(v1, v2), (v2, v1), (v1, v3), (v3, v1), (v2, v3), (v3, v2), (v3, v4), (v4, v3)}
해당 표기는 엣지에 방향이 있는 그래프가 좀 더 적합하다.
2. 그래프의 종류
무방향 그래프(Nondirected Graph): 간선을 통해서 양 방향으로 이동할 수 있는 그래프
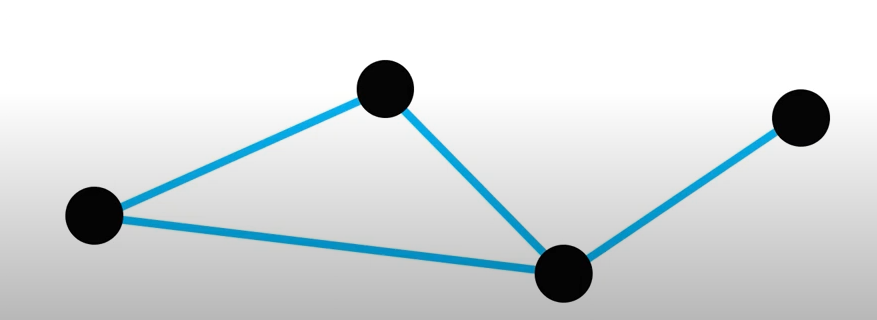
- (v1, v2) == (v2, v1)
참조: https://junstar92.tistory.com/196
방향 그래프(Directed Graph): 간선의 방향성이 존재하는 그래프
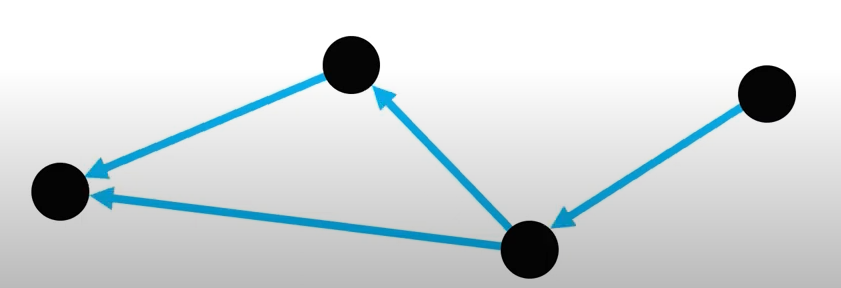
- (v1, v2) != (v2, v1)
참조: https://junstar92.tistory.com/196
완전 그래프(Complete Graph): 모든 정점이 서로 연결되어 있는 그래프
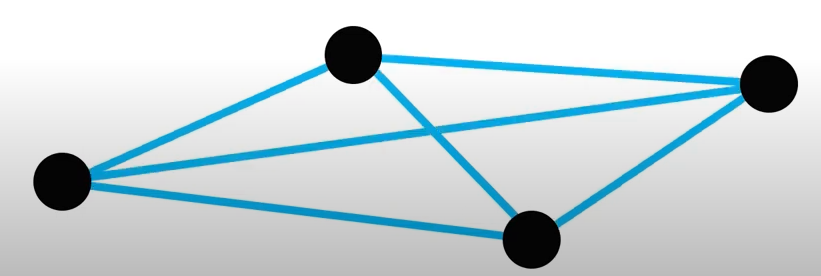
- 간선의 수는 n(n-1)/2이다.
다중 그래프(Multi Graph): '루프' 및 '다중 간선'이 존재하는 그래프
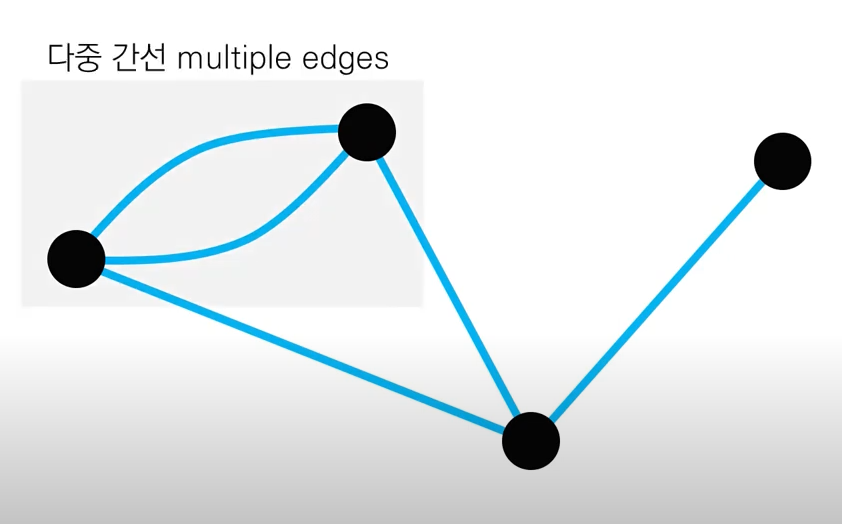
- 다중 간선(Multiple Edges): 해당 그래프처럼 두 정점 쌍을 여러 개의 노선이 연결하는 것
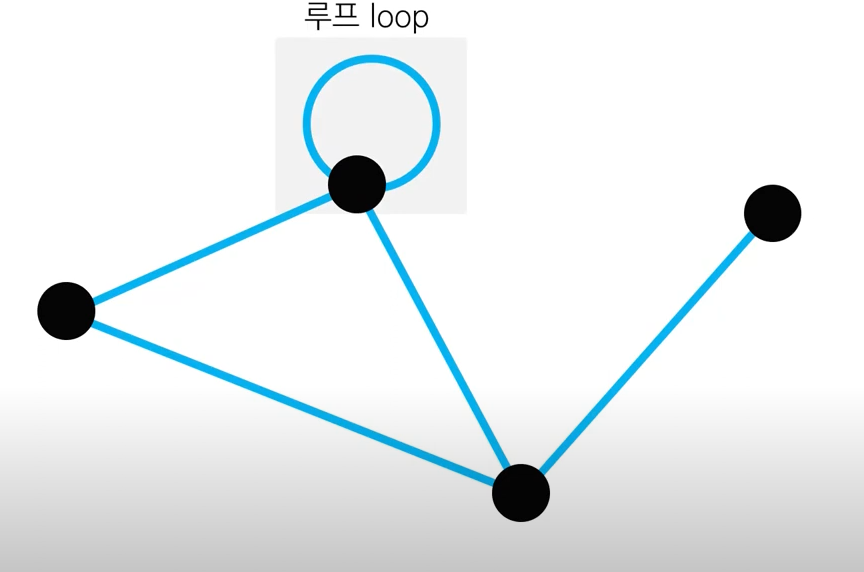
- 루프(Loop): 한 정점에서 나와 똑같은 정점에 연결되는 것
연결 그래프(Connected Graph): 무방향 그래프에서 모든 정점이 직, 간접적으로 연결되어 있는 그래프
가중치 그래프(Weighted Graph): 간선에 숫자로 된 가중치를 각 간선에 부여하는 그래프
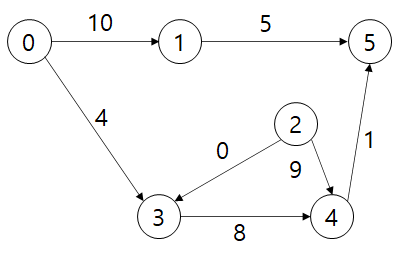
참조: https://junstar92.tistory.com/198
3. 그래프 관련 용어
- 인접(adjacent): 두 정점을 연결하면 간선이 존재한다.
- 부속(incident): 인접한 두 정점 사이의 간선을 두 정점에 부속되었다고 한다.
- 차수(degree): 정점에 부속되어 있는 간선의 수를 말한다. 무방향 그래프에서는 단순히 정점에 연결된 간선의 수를 뜻하지만, 방향 그래프에서는 진입 차수(in-degree)와 진출 차수(out-degree)로 나눈다.
- 경로(path): 그래프에서 간선을 따라 갈 수 있는 길을 정점으로 나열한 것이다.
- 경로 길이(path length): 경로를 구성하는 간선의 수
- 단순 경로(simple path): 모두 다른 정점으로 구성된 경로
- 사이클(cycle): 한 정점에서 시작해 같은 정점으로 끝나는 경로
- DAG(Directed Acyclic Graph): 방향 그래프이면서 사이클이 존재하지 않는 그래프.
4. 그래프의 표현
인접 행렬(Adjacency Matrix): 2차원 배열을 사용하여 그래프를 표현하며 모든 정보를 저장한다.
3-1. 방향그래프
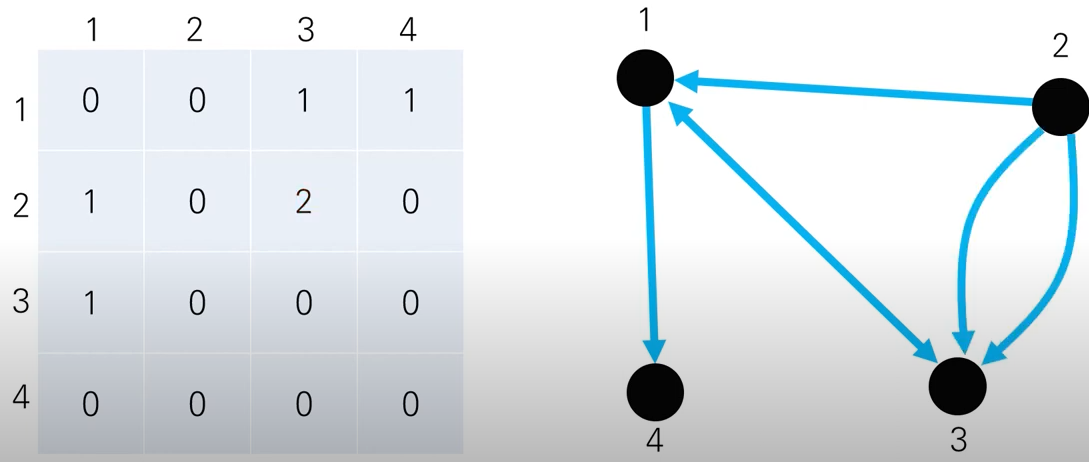
3-2. 무방향 그래프
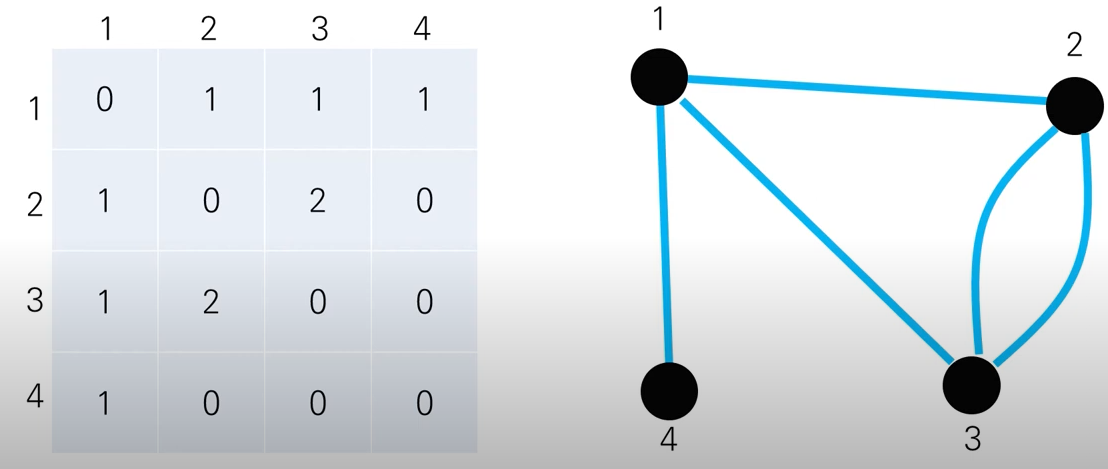
한 행의 원소를 모두 더하면 out-degree(한 정점에서 나가는 엣지)가 된다.
한 열의 원소를 모두 더하면 in-degree(한 정점으로 들어오는 엣지)가 된다.
인접 행렬을 제곱하면 해당 그래프의 경로 길이에 대한 정보를 얻을 수 있다.
대각선에 대해서 대칭 행렬이 되며, 특히 단순 그래프의 인접 행렬은 Binary Matrix가 된다.
장점
- 두 정점을 연결하는 간선의 여부와 가중치 값은 배열에 직접 접근하면 바로 확인 할 수 있다.
- 배열 위치를 확인하면 두 정점에 대한 연결 정보를 조회할 때, O(1)의 시간 복잡도면 가능하다.
- 구현이 비교적 간편하다.
단점
- 정점의 개수에 비해 간선이 적을 때는 공간 효율성이 떨어진다.
- 불필요한 정보의 저장이 많으며, 그래프의 크기가 커지면 메모리 초과가 발생할 수 있다.
- 모든 정점에 대해 간선 정보를 대입해야 하므로, O(n^2)의 시간 복잡도가 소요된다.
코드
import sys
input = sys.stdin.readline
vertex, edge = map(int, input().split())
adj = [[0 for _ in range(vertex)] for _ in range(vertex)]
for _ in range(edge):
src, dest = map(int, input().split())
adj[src][dest] = 1
adj[dest][src] = 1인접 리스트(Adjacency List): 연결 리스트들의 배열로 표현하며 갈 수 있는 곳만 정보를 저장한다.
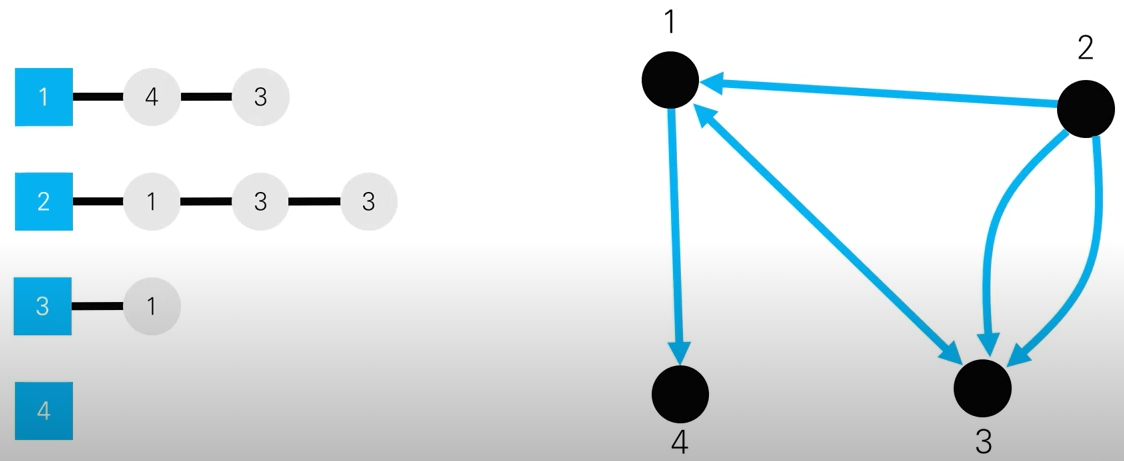
장점
- 메모리 절약 가능하다.
- 희소 그래프(정점보다 간선의 갯수가 적은 그래프)를 표현하는데 유리하다.
- 정점들의 연결 정보를 탐색할 때, O(n)의 시간이면 가능하다.
단점
- 특정 두 점이 연결되었는지 확인하려면 인접 행렬에 비해 시간이 오래 걸린다.(배열보다 search 속도 느림)
- 구현이 비교적 어렵다.
코드
import sys
input = sys.stdin.readline
vertex, edge = map(int, input().split())
adj = [ [] for _ in range(vertex)]
for _ in range(edge):
src, dest = map(int, input().split())
adj[src].append(dest)
adj[dest].append(src)